
Question Number 17472 by Arnab Maiti last updated on 06/Jul/17
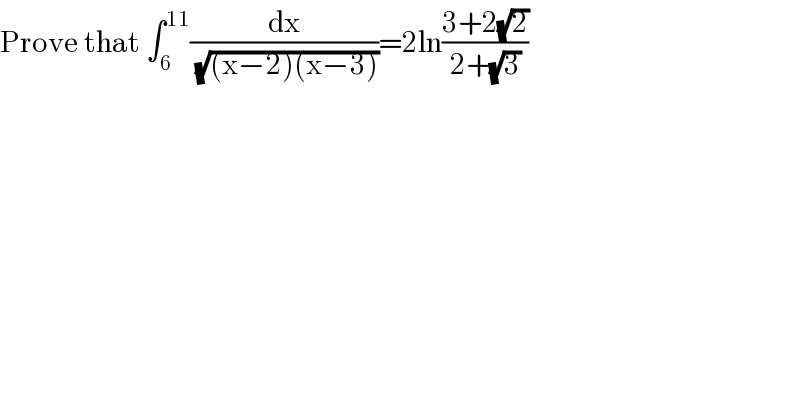
$$\mathrm{Prove}\:\mathrm{that}\:\int_{\mathrm{6}} ^{\mathrm{11}} \frac{\mathrm{dx}}{\sqrt{\left(\mathrm{x}−\mathrm{2}\right)\left(\mathrm{x}−\mathrm{3}\right)}}=\mathrm{2ln}\frac{\mathrm{3}+\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{2}+\sqrt{\mathrm{3}}} \\ $$
Answered by sma3l2996 last updated on 06/Jul/17
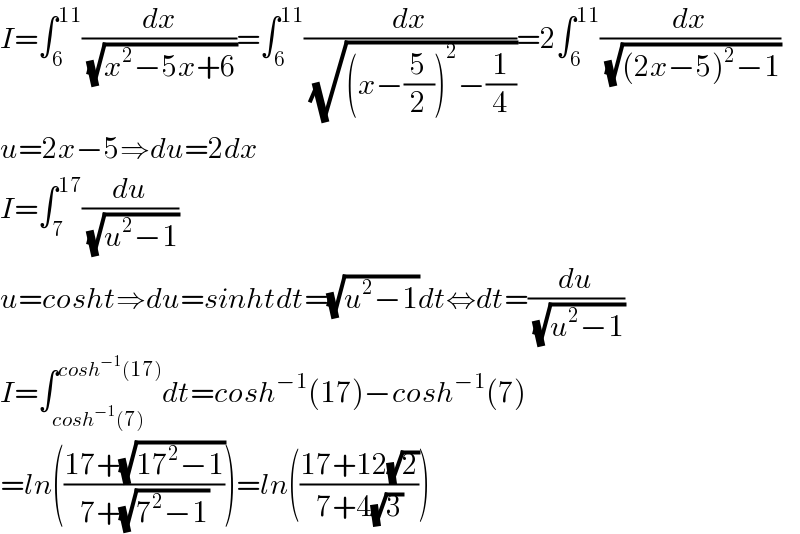
$${I}=\int_{\mathrm{6}} ^{\mathrm{11}} \frac{{dx}}{\sqrt{{x}^{\mathrm{2}} −\mathrm{5}{x}+\mathrm{6}}}=\int_{\mathrm{6}} ^{\mathrm{11}} \frac{{dx}}{\sqrt{\left({x}−\frac{\mathrm{5}}{\mathrm{2}}\right)^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{4}}}}=\mathrm{2}\int_{\mathrm{6}} ^{\mathrm{11}} \frac{{dx}}{\sqrt{\left(\mathrm{2}{x}−\mathrm{5}\right)^{\mathrm{2}} −\mathrm{1}}} \\ $$$${u}=\mathrm{2}{x}−\mathrm{5}\Rightarrow{du}=\mathrm{2}{dx} \\ $$$${I}=\int_{\mathrm{7}} ^{\mathrm{17}} \frac{{du}}{\sqrt{{u}^{\mathrm{2}} −\mathrm{1}}} \\ $$$${u}={cosht}\Rightarrow{du}={sinhtdt}=\sqrt{{u}^{\mathrm{2}} −\mathrm{1}}{dt}\Leftrightarrow{dt}=\frac{{du}}{\sqrt{{u}^{\mathrm{2}} −\mathrm{1}}} \\ $$$${I}=\int_{{cosh}^{−\mathrm{1}} \left(\mathrm{7}\right)} ^{{cosh}^{−\mathrm{1}} \left(\mathrm{17}\right)} {dt}={cosh}^{−\mathrm{1}} \left(\mathrm{17}\right)−{cosh}^{−\mathrm{1}} \left(\mathrm{7}\right) \\ $$$$={ln}\left(\frac{\mathrm{17}+\sqrt{\mathrm{17}^{\mathrm{2}} −\mathrm{1}}}{\mathrm{7}+\sqrt{\mathrm{7}^{\mathrm{2}} −\mathrm{1}}}\right)={ln}\left(\frac{\mathrm{17}+\mathrm{12}\sqrt{\mathrm{2}}}{\mathrm{7}+\mathrm{4}\sqrt{\mathrm{3}}}\right) \\ $$
Commented by Arnab Maiti last updated on 07/Jul/17
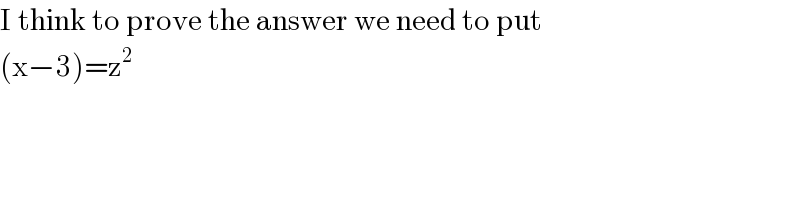
$$\mathrm{I}\:\mathrm{think}\:\mathrm{to}\:\mathrm{prove}\:\mathrm{the}\:\mathrm{answer}\:\mathrm{we}\:\mathrm{need}\:\mathrm{to}\:\mathrm{put} \\ $$$$\left(\mathrm{x}−\mathrm{3}\right)=\mathrm{z}^{\mathrm{2}} \\ $$
