
Question Number 35004 by Rasheed.Sindhi last updated on 14/May/18
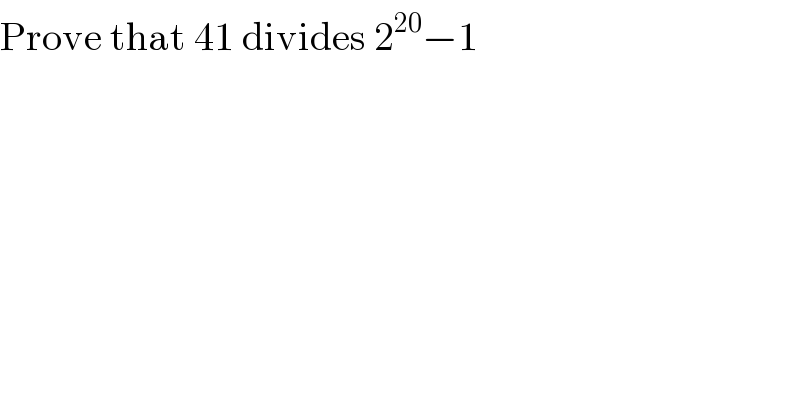
$$\mathrm{Prove}\:\mathrm{that}\:\mathrm{41}\:\mathrm{divides}\:\mathrm{2}^{\mathrm{20}} −\mathrm{1} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 14/May/18
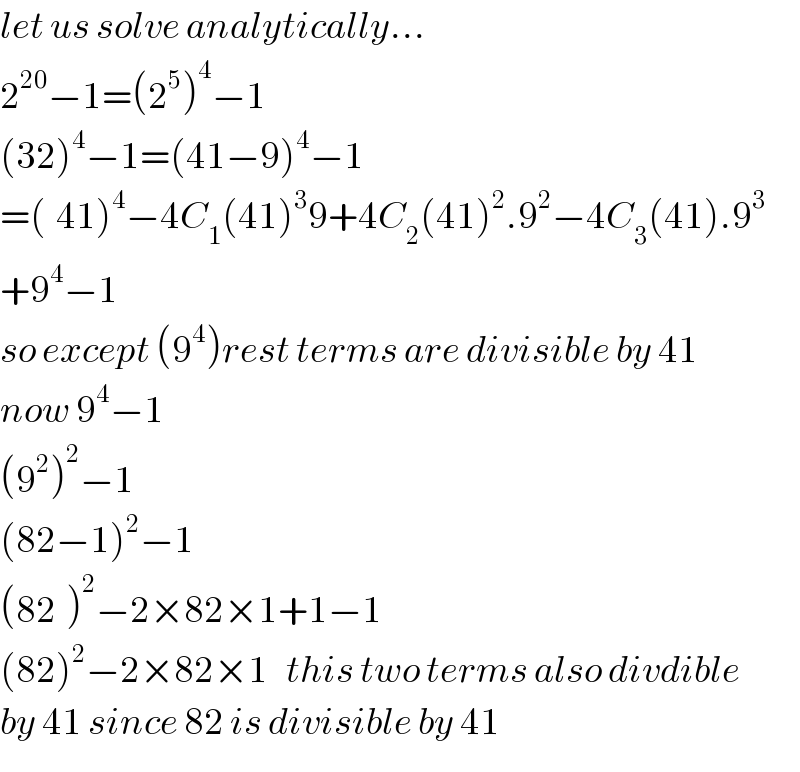
$${let}\:{us}\:{solve}\:{analytically}... \\ $$$$\mathrm{2}^{\mathrm{20}} −\mathrm{1}=\left(\mathrm{2}^{\mathrm{5}} \right)^{\mathrm{4}} −\mathrm{1} \\ $$$$\left(\mathrm{32}\right)^{\mathrm{4}} −\mathrm{1}=\left(\mathrm{41}−\mathrm{9}\right)^{\mathrm{4}} −\mathrm{1} \\ $$$$=\left(_{} \mathrm{41}\right)^{\mathrm{4}} −\mathrm{4}{C}_{\mathrm{1}} \left(\mathrm{41}\right)^{\mathrm{3}} \mathrm{9}+\mathrm{4}{C}_{\mathrm{2}} \left(\mathrm{41}\right)^{\mathrm{2}} .\mathrm{9}^{\mathrm{2}} −\mathrm{4}{C}_{\mathrm{3}} \left(\mathrm{41}\right).\mathrm{9}^{\mathrm{3}} \\ $$$$+\mathrm{9}^{\mathrm{4}} −\mathrm{1} \\ $$$${so}\:{except}\:\left(\mathrm{9}^{\mathrm{4}} \right){rest}\:{terms}\:{are}\:{divisible}\:{by}\:\mathrm{41} \\ $$$${now}\:\mathrm{9}^{\mathrm{4}} −\mathrm{1} \\ $$$$\left(\mathrm{9}^{\mathrm{2}} \right)^{\mathrm{2}} −\mathrm{1} \\ $$$$\left(\mathrm{82}−\mathrm{1}\right)^{\mathrm{2}} −\mathrm{1} \\ $$$$\left(\mathrm{82}^{} \right)^{\mathrm{2}} −\mathrm{2}×\mathrm{82}×\mathrm{1}+\mathrm{1}−\mathrm{1} \\ $$$$\left(\mathrm{82}\right)^{\mathrm{2}} −\mathrm{2}×\mathrm{82}×\mathrm{1}\:\:\:{this}\:{two}\:{terms}\:{also}\:{divdible} \\ $$$${by}\:\mathrm{41}\:{since}\:\mathrm{82}\:{is}\:{divisible}\:{by}\:\mathrm{41} \\ $$
Commented by Rasheed.Sindhi last updated on 15/May/18

$$\mathcal{G}^{\:\overset{\frown} {\mathcal{O}}\overset{\frown} {\mathcal{O}}} \mathcal{D}\:\mathcal{A}{pproach}! \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 15/May/18

$${thanx}...{we}\:{can}\:{post}\:{question}\:{along}\:{with}\: \\ $$$${final}\:{answer}\:{so}\:{that}\:{we}\:{get}\:{satisfaction}... \\ $$$${the}\:{people}\:{who}\:{post}\:{question}\:{may}\:{post}\:{question} \\ $$$${different}\:{variety}... \\ $$
Answered by MJS last updated on 14/May/18
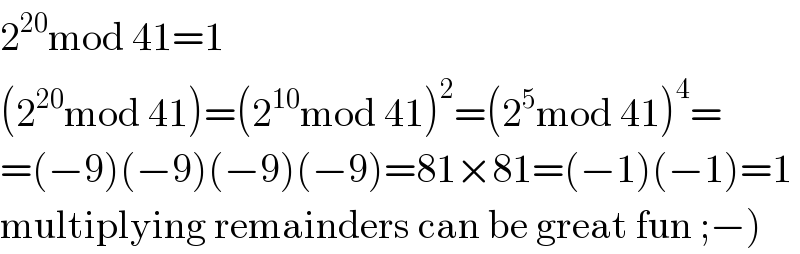
$$\mathrm{2}^{\mathrm{20}} \mathrm{mod}\:\mathrm{41}=\mathrm{1} \\ $$$$\left(\mathrm{2}^{\mathrm{20}} \mathrm{mod}\:\mathrm{41}\right)=\left(\mathrm{2}^{\mathrm{10}} \mathrm{mod}\:\mathrm{41}\right)^{\mathrm{2}} =\left(\mathrm{2}^{\mathrm{5}} \mathrm{mod}\:\mathrm{41}\right)^{\mathrm{4}} = \\ $$$$=\left(−\mathrm{9}\right)\left(−\mathrm{9}\right)\left(−\mathrm{9}\right)\left(−\mathrm{9}\right)=\mathrm{81}×\mathrm{81}=\left(−\mathrm{1}\right)\left(−\mathrm{1}\right)=\mathrm{1} \\ $$$$\left.\mathrm{multiplying}\:\mathrm{remainders}\:\mathrm{can}\:\mathrm{be}\:\mathrm{great}\:\mathrm{fun}\:;−\right) \\ $$
Commented by Rasheed.Sindhi last updated on 15/May/18

$$\mathcal{V}_{{r}} ^{\:{e}} {y}\:\mathcal{N}{ice}!... \\ $$$$\mathrm{But}\:\mathrm{using}\:\mathrm{congruence}\:\mathrm{notation}\:\mathrm{were} \\ $$$$\mathrm{easier}\:\mathrm{and}\:\mathrm{prettier},\:\mathrm{I}\:\mathrm{think}. \\ $$
Commented by MJS last updated on 14/May/18

$$\mathrm{true} \\ $$
Answered by ajfour last updated on 14/May/18
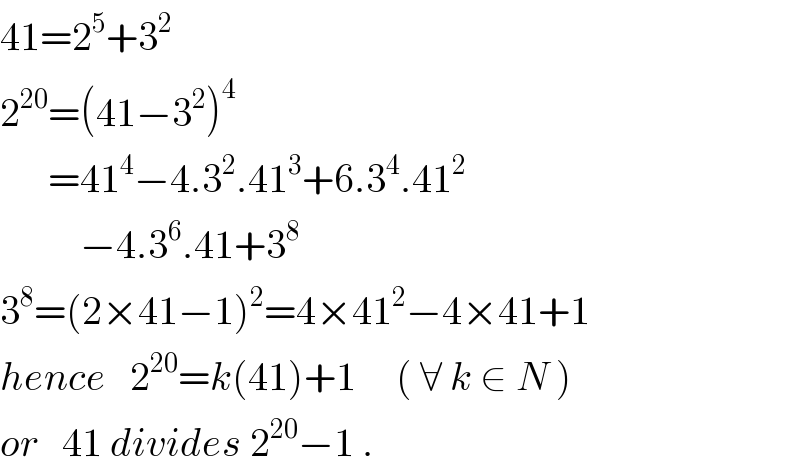
$$\mathrm{41}=\mathrm{2}^{\mathrm{5}} +\mathrm{3}^{\mathrm{2}} \\ $$$$\mathrm{2}^{\mathrm{20}} =\left(\mathrm{41}−\mathrm{3}^{\mathrm{2}} \right)^{\mathrm{4}} \\ $$$$\:\:\:\:\:\:=\mathrm{41}^{\mathrm{4}} −\mathrm{4}.\mathrm{3}^{\mathrm{2}} .\mathrm{41}^{\mathrm{3}} +\mathrm{6}.\mathrm{3}^{\mathrm{4}} .\mathrm{41}^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:−\mathrm{4}.\mathrm{3}^{\mathrm{6}} .\mathrm{41}+\mathrm{3}^{\mathrm{8}} \\ $$$$\mathrm{3}^{\mathrm{8}} =\left(\mathrm{2}×\mathrm{41}−\mathrm{1}\right)^{\mathrm{2}} =\mathrm{4}×\mathrm{41}^{\mathrm{2}} −\mathrm{4}×\mathrm{41}+\mathrm{1} \\ $$$${hence}\:\:\:\mathrm{2}^{\mathrm{20}} ={k}\left(\mathrm{41}\right)+\mathrm{1}\:\:\:\:\:\left(\:\forall\:{k}\:\in\:{N}\:\right) \\ $$$${or}\:\:\:\mathrm{41}\:{divides}\:\mathrm{2}^{\mathrm{20}} −\mathrm{1}\:. \\ $$
Commented by Rasheed.Sindhi last updated on 15/May/18
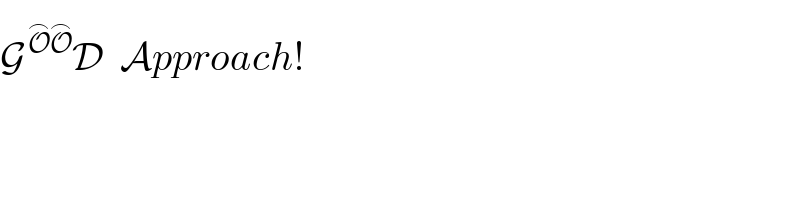
$$\mathcal{G}^{\:\overset{\frown} {\mathcal{O}}\overset{\frown} {\mathcal{O}}} \mathcal{D}\:\:\mathcal{A}{pproach}! \\ $$
