
Question Number 143708 by ZiYangLee last updated on 17/Jun/21
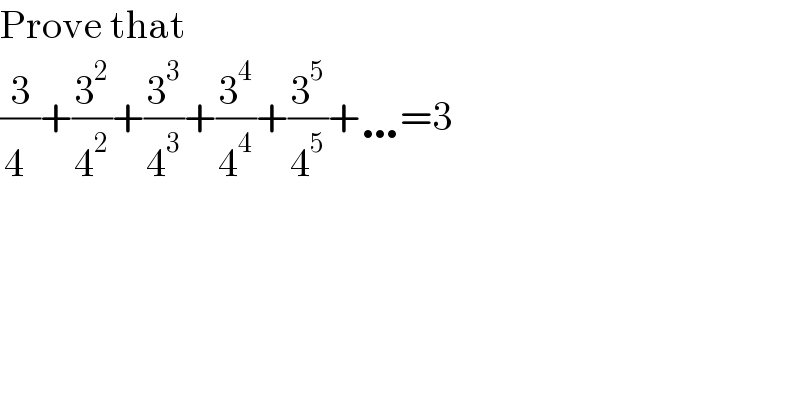
$$\mathrm{Prove}\:\mathrm{that} \\ $$$$\frac{\mathrm{3}}{\mathrm{4}^{} }+\frac{\mathrm{3}^{\mathrm{2}} }{\mathrm{4}^{\mathrm{2}} }+\frac{\mathrm{3}^{\mathrm{3}} }{\mathrm{4}^{\mathrm{3}} }+\frac{\mathrm{3}^{\mathrm{4}} }{\mathrm{4}^{\mathrm{4}} }+\frac{\mathrm{3}^{\mathrm{5}} }{\mathrm{4}^{\mathrm{5}} }+\ldots=\mathrm{3} \\ $$
Answered by som(math1967) last updated on 17/Jun/21
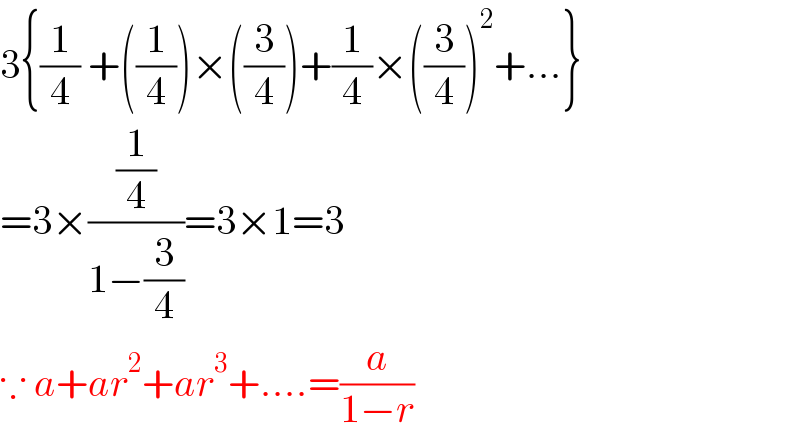
$$\mathrm{3}\left\{\frac{\mathrm{1}}{\mathrm{4}}\:+\left(\frac{\mathrm{1}}{\mathrm{4}}\right)×\left(\frac{\mathrm{3}}{\mathrm{4}}\right)+\frac{\mathrm{1}}{\mathrm{4}}×\left(\frac{\mathrm{3}}{\mathrm{4}}\right)^{\mathrm{2}} +...\right\} \\ $$$$=\mathrm{3}×\frac{\frac{\mathrm{1}}{\mathrm{4}}}{\mathrm{1}−\frac{\mathrm{3}}{\mathrm{4}}}=\mathrm{3}×\mathrm{1}=\mathrm{3}\: \\ $$$$\because\:{a}+{ar}^{\mathrm{2}} +{ar}^{\mathrm{3}} +....=\frac{{a}}{\mathrm{1}−{r}} \\ $$
Answered by Dwaipayan Shikari last updated on 17/Jun/21
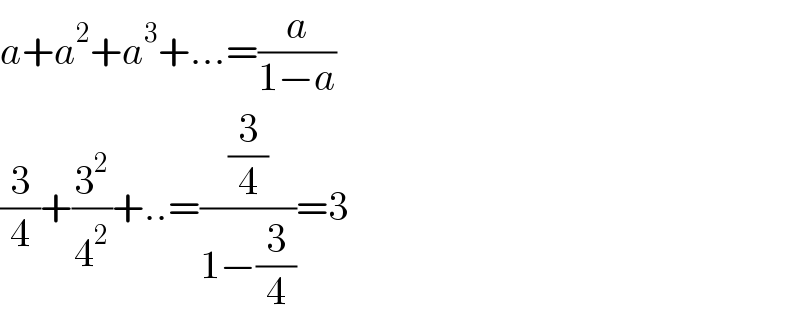
$${a}+{a}^{\mathrm{2}} +{a}^{\mathrm{3}} +...=\frac{{a}}{\mathrm{1}−{a}} \\ $$$$\frac{\mathrm{3}}{\mathrm{4}}+\frac{\mathrm{3}^{\mathrm{2}} }{\mathrm{4}^{\mathrm{2}} }+..=\frac{\frac{\mathrm{3}}{\mathrm{4}}}{\mathrm{1}−\frac{\mathrm{3}}{\mathrm{4}}}=\mathrm{3} \\ $$
Answered by Willson last updated on 17/Jun/21
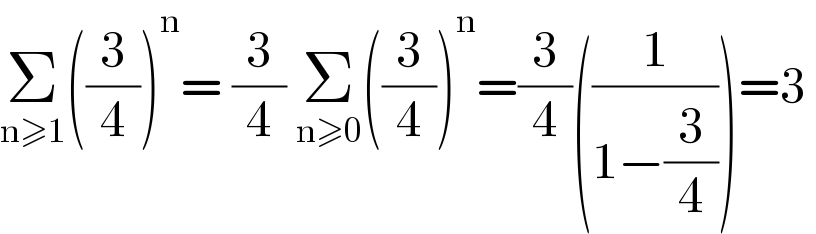
$$\underset{\mathrm{n}\geqslant\mathrm{1}} {\sum}\left(\frac{\mathrm{3}}{\mathrm{4}}\right)^{\mathrm{n}} =\:\frac{\mathrm{3}}{\mathrm{4}}\:\underset{\mathrm{n}\geqslant\mathrm{0}} {\sum}\left(\frac{\mathrm{3}}{\mathrm{4}}\right)^{\mathrm{n}} =\frac{\mathrm{3}}{\mathrm{4}}\left(\frac{\mathrm{1}}{\mathrm{1}−\frac{\mathrm{3}}{\mathrm{4}}}\right)=\mathrm{3}\: \\ $$
