Question and Answers Forum

All Questions      Topic List

Trigonometry Questions

Previous in All Question      Next in All Question      

Previous in Trigonometry      Next in Trigonometry      

Question Number 126562 by mey3nipaba last updated on 21/Dec/20

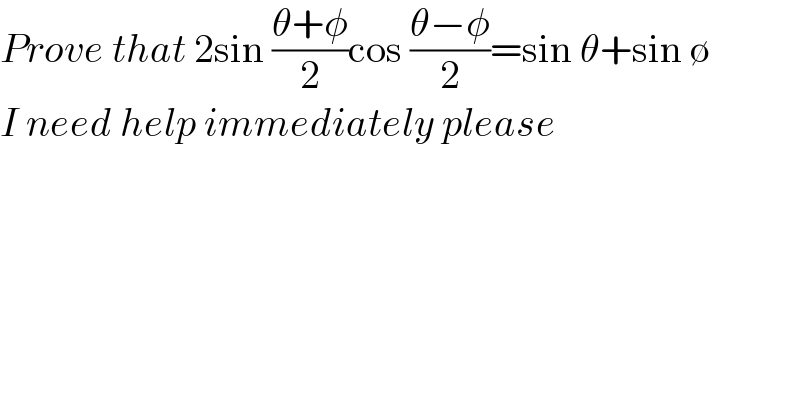
Prove that 2sin ((θ+φ)/2)cos ((θ−φ)/2)=sin θ+sin ∅ I need help immediately please

$${Prove}\:{that}\:\mathrm{2sin}\:\frac{\theta+\phi}{\mathrm{2}}\mathrm{cos}\:\frac{\theta−\phi}{\mathrm{2}}=\mathrm{sin}\:\theta+\mathrm{sin}\:\emptyset \\ $$$${I}\:{need}\:{help}\:{immediately}\:{please} \\ $$

Commented by mr W last updated on 21/Dec/20

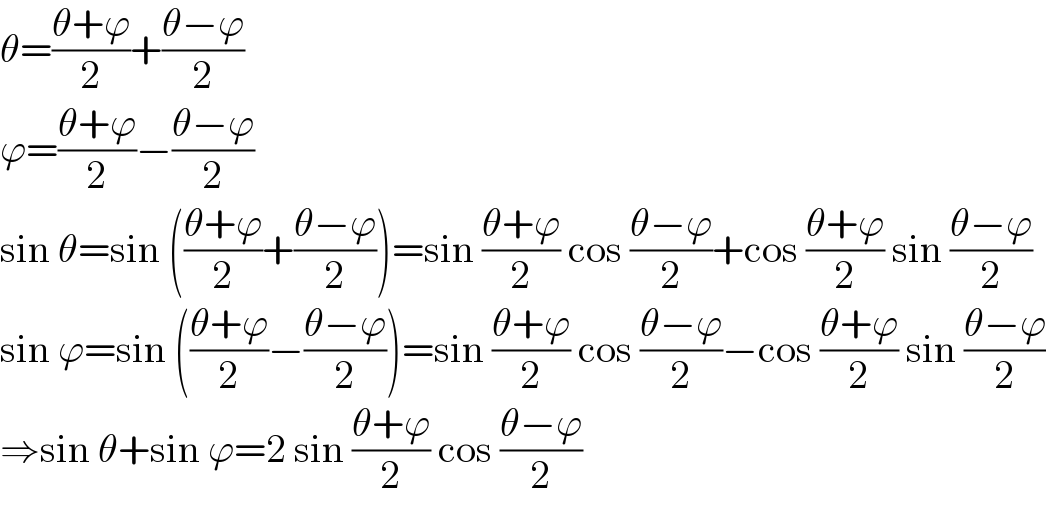
θ=((θ+ϕ)/2)+((θ−ϕ)/2) ϕ=((θ+ϕ)/2)−((θ−ϕ)/2) sin θ=sin (((θ+ϕ)/2)+((θ−ϕ)/2))=sin ((θ+ϕ)/2) cos ((θ−ϕ)/2)+cos ((θ+ϕ)/2) sin ((θ−ϕ)/2) sin ϕ=sin (((θ+ϕ)/2)−((θ−ϕ)/2))=sin ((θ+ϕ)/2) cos ((θ−ϕ)/2)−cos ((θ+ϕ)/2) sin ((θ−ϕ)/2) ⇒sin θ+sin ϕ=2 sin ((θ+ϕ)/2) cos ((θ−ϕ)/2)

$$\theta=\frac{\theta+\varphi}{\mathrm{2}}+\frac{\theta−\varphi}{\mathrm{2}} \\ $$$$\varphi=\frac{\theta+\varphi}{\mathrm{2}}−\frac{\theta−\varphi}{\mathrm{2}} \\ $$$$\mathrm{sin}\:\theta=\mathrm{sin}\:\left(\frac{\theta+\varphi}{\mathrm{2}}+\frac{\theta−\varphi}{\mathrm{2}}\right)=\mathrm{sin}\:\frac{\theta+\varphi}{\mathrm{2}}\:\mathrm{cos}\:\frac{\theta−\varphi}{\mathrm{2}}+\mathrm{cos}\:\frac{\theta+\varphi}{\mathrm{2}}\:\mathrm{sin}\:\frac{\theta−\varphi}{\mathrm{2}} \\ $$$$\mathrm{sin}\:\varphi=\mathrm{sin}\:\left(\frac{\theta+\varphi}{\mathrm{2}}−\frac{\theta−\varphi}{\mathrm{2}}\right)=\mathrm{sin}\:\frac{\theta+\varphi}{\mathrm{2}}\:\mathrm{cos}\:\frac{\theta−\varphi}{\mathrm{2}}−\mathrm{cos}\:\frac{\theta+\varphi}{\mathrm{2}}\:\mathrm{sin}\:\frac{\theta−\varphi}{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{sin}\:\theta+\mathrm{sin}\:\varphi=\mathrm{2}\:\mathrm{sin}\:\frac{\theta+\varphi}{\mathrm{2}}\:\mathrm{cos}\:\frac{\theta−\varphi}{\mathrm{2}} \\ $$

Answered by Olaf last updated on 21/Dec/20

Many ways to prove that. Example : Let f_φ (θ) = 2sin((θ+φ)/2)cos((θ−φ)/2) and g_φ (θ) = sinθ+sinφ (φ is a parameter) f_φ ′(θ) = 2[(1/2)cos((θ+φ)/2)cos((θ−φ)/2)−(1/2)sin((θ+φ)/2)cos((θ+φ)/2)] f_φ ′(θ) = cos(((θ+φ)/2)+((θ−φ)/2)) = cosθ = g_φ ′(θ) ⇒ f_φ (θ) = g_φ (θ)+C C = f_φ (φ) −g_φ (φ) = 2sinφ−2sinφ = 0 f_φ (θ) = g_φ (θ)

$$\mathrm{Many}\:\mathrm{ways}\:\mathrm{to}\:\mathrm{prove}\:\mathrm{that}. \\ $$$$\mathrm{Example}\:: \\ $$$$\mathrm{Let}\:{f}_{\phi} \left(\theta\right)\:=\:\mathrm{2sin}\frac{\theta+\phi}{\mathrm{2}}\mathrm{cos}\frac{\theta−\phi}{\mathrm{2}} \\ $$$$\mathrm{and}\:{g}_{\phi} \left(\theta\right)\:=\:\mathrm{sin}\theta+\mathrm{sin}\phi \\ $$$$\left(\phi\:\mathrm{is}\:\mathrm{a}\:\mathrm{parameter}\right) \\ $$$${f}_{\phi} '\left(\theta\right)\:=\:\mathrm{2}\left[\frac{\mathrm{1}}{\mathrm{2}}\mathrm{cos}\frac{\theta+\phi}{\mathrm{2}}\mathrm{cos}\frac{\theta−\phi}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}\frac{\theta+\phi}{\mathrm{2}}\mathrm{cos}\frac{\theta+\phi}{\mathrm{2}}\right] \\ $$$${f}_{\phi} '\left(\theta\right)\:=\:\mathrm{cos}\left(\frac{\theta+\phi}{\mathrm{2}}+\frac{\theta−\phi}{\mathrm{2}}\right)\:=\:\mathrm{cos}\theta\:=\:{g}_{\phi} '\left(\theta\right) \\ $$$$\Rightarrow\:{f}_{\phi} \left(\theta\right)\:=\:{g}_{\phi} \left(\theta\right)+\mathrm{C} \\ $$$$\mathrm{C}\:=\:{f}_{\phi} \left(\phi\right)\:−{g}_{\phi} \left(\phi\right)\:=\:\mathrm{2sin}\phi−\mathrm{2sin}\phi\:=\:\mathrm{0} \\ $$$${f}_{\phi} \left(\theta\right)\:=\:{g}_{\phi} \left(\theta\right) \\ $$

Answered by physicstutes last updated on 21/Dec/20

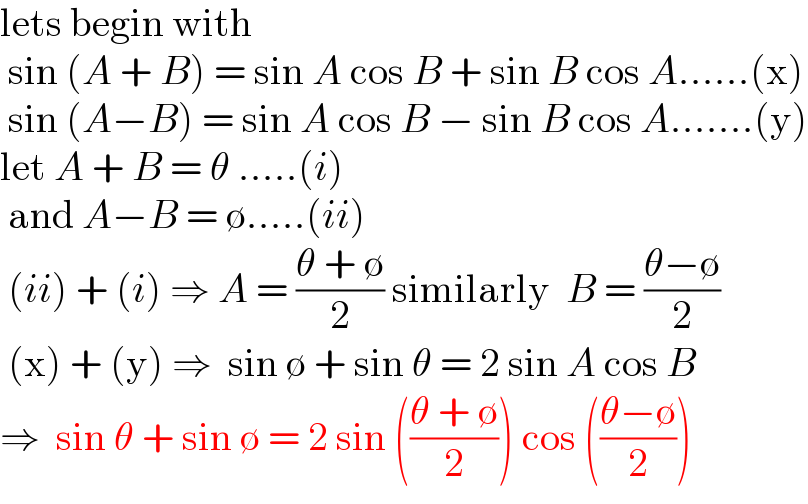
lets begin with sin (A + B) = sin A cos B + sin B cos A......(x) sin (A−B) = sin A cos B − sin B cos A.......(y) let A + B = θ .....(i) and A−B = ∅.....(ii) (ii) + (i) ⇒ A = ((θ + ∅)/2) similarly B = ((θ−∅)/2) (x) + (y) ⇒ sin ∅ + sin θ = 2 sin A cos B ⇒ sin θ + sin ∅ = 2 sin (((θ + ∅)/2)) cos (((θ−∅)/2))

$$\mathrm{lets}\:\mathrm{begin}\:\mathrm{with} \\ $$$$\:\mathrm{sin}\:\left({A}\:+\:{B}\right)\:=\:\mathrm{sin}\:{A}\:\mathrm{cos}\:{B}\:+\:\mathrm{sin}\:{B}\:\mathrm{cos}\:{A}......\left(\mathrm{x}\right) \\ $$$$\:\mathrm{sin}\:\left({A}−{B}\right)\:=\:\mathrm{sin}\:{A}\:\mathrm{cos}\:{B}\:−\:\mathrm{sin}\:{B}\:\mathrm{cos}\:{A}.......\left(\mathrm{y}\right) \\ $$$$\mathrm{let}\:{A}\:+\:{B}\:=\:\theta\:.....\left({i}\right) \\ $$$$\:\mathrm{and}\:{A}−{B}\:=\:\emptyset.....\left({ii}\right) \\ $$$$\:\left({ii}\right)\:+\:\left({i}\right)\:\Rightarrow\:{A}\:=\:\frac{\theta\:+\:\emptyset}{\mathrm{2}}\:\mathrm{similarly}\:\:{B}\:=\:\frac{\theta−\emptyset}{\mathrm{2}} \\ $$$$\:\left(\mathrm{x}\right)\:+\:\left(\mathrm{y}\right)\:\Rightarrow\:\:\mathrm{sin}\:\emptyset\:+\:\mathrm{sin}\:\theta\:=\:\mathrm{2}\:\mathrm{sin}\:{A}\:\mathrm{cos}\:{B} \\ $$$$\Rightarrow\:\:\mathrm{sin}\:\theta\:+\:\mathrm{sin}\:\emptyset\:=\:\mathrm{2}\:\mathrm{sin}\:\left(\frac{\theta\:+\:\emptyset}{\mathrm{2}}\right)\:\mathrm{cos}\:\left(\frac{\theta−\emptyset}{\mathrm{2}}\right) \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com