
Question Number 216914 by hardmath last updated on 24/Feb/25
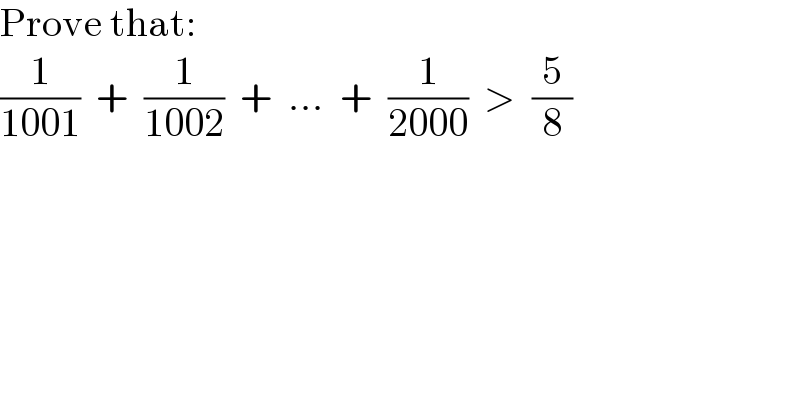
$$\mathrm{Prove}\:\mathrm{that}: \\ $$$$\frac{\mathrm{1}}{\mathrm{1001}}\:\:+\:\:\frac{\mathrm{1}}{\mathrm{1002}}\:\:+\:\:...\:\:+\:\:\frac{\mathrm{1}}{\mathrm{2000}}\:\:>\:\:\frac{\mathrm{5}}{\mathrm{8}} \\ $$
Answered by MrGaster last updated on 24/Feb/25
![Σ_(k=1001) ^(2000) (1/k)>(5/8) ∫_(1001) ^(2001) (1/x)dx>(5/8) ln(20001)−ln(1001)>(5/8) ln(((2001)/(1001)))>(5/8) ln(2.000999)>(5/8) 0.693147>0.626 [Q.E.D]](Q216915.png)
$$\underset{{k}=\mathrm{1001}} {\overset{\mathrm{2000}} {\sum}}\frac{\mathrm{1}}{{k}}>\frac{\mathrm{5}}{\mathrm{8}} \\ $$$$\int_{\mathrm{1001}} ^{\mathrm{2001}} \frac{\mathrm{1}}{{x}}{dx}>\frac{\mathrm{5}}{\mathrm{8}} \\ $$$$\mathrm{ln}\left(\mathrm{20001}\right)−\mathrm{ln}\left(\mathrm{1001}\right)>\frac{\mathrm{5}}{\mathrm{8}} \\ $$$$\mathrm{ln}\left(\frac{\mathrm{2001}}{\mathrm{1001}}\right)>\frac{\mathrm{5}}{\mathrm{8}} \\ $$$$\mathrm{ln}\left(\mathrm{2}.\mathrm{000999}\right)>\frac{\mathrm{5}}{\mathrm{8}} \\ $$$$\mathrm{0}.\mathrm{693147}>\mathrm{0}.\mathrm{626} \\ $$$$\left[\mathrm{Q}.\mathrm{E}.\mathrm{D}\right] \\ $$
Commented by mehdee7396 last updated on 25/Feb/25
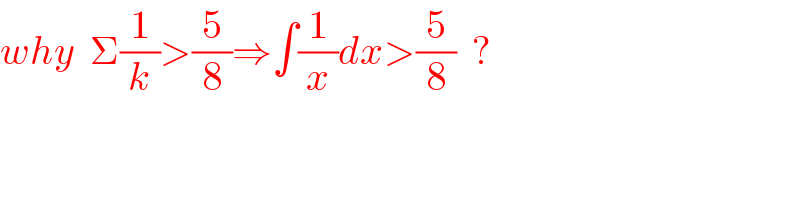
$${why}\:\:\Sigma\frac{\mathrm{1}}{{k}}>\frac{\mathrm{5}}{\mathrm{8}}\Rightarrow\int\frac{\mathrm{1}}{{x}}{dx}>\frac{\mathrm{5}}{\mathrm{8}}\:\:? \\ $$$$ \\ $$
Answered by mehdee7396 last updated on 25/Feb/25
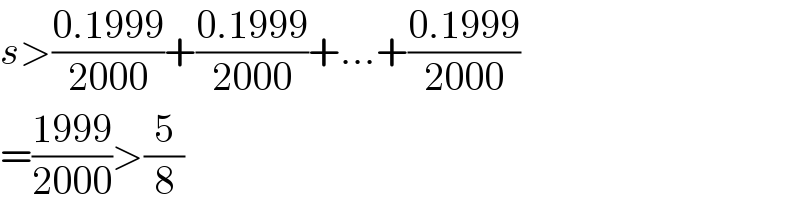
$${s}>\frac{\mathrm{0}.\mathrm{1999}}{\mathrm{2000}}+\frac{\mathrm{0}.\mathrm{1999}}{\mathrm{2000}}+...+\frac{\mathrm{0}.\mathrm{1999}}{\mathrm{2000}} \\ $$$$=\frac{\mathrm{1999}}{\mathrm{2000}}>\frac{\mathrm{5}}{\mathrm{8}} \\ $$
