
Previous in Differential Equation Next in Differential Equation
Question Number 197113 by Erico last updated on 08/Sep/23
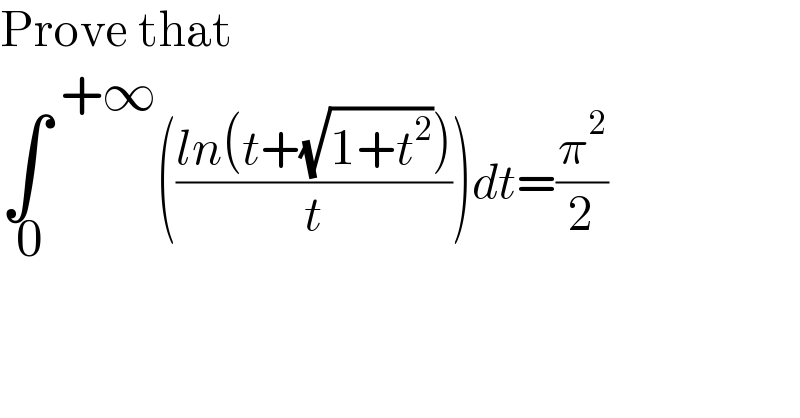
$$\mathrm{Prove}\:\mathrm{that} \\ $$$$\underset{\:\mathrm{0}} {\int}^{\:+\infty} \left(\frac{{ln}\left({t}+\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }\right)}{{t}}\right){dt}=\frac{\pi^{\mathrm{2}} }{\mathrm{2}} \\ $$
Answered by witcher3 last updated on 08/Sep/23
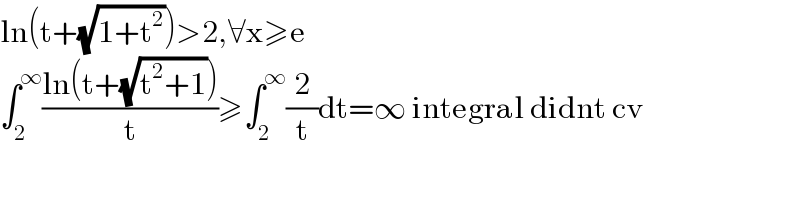
$$\mathrm{ln}\left(\mathrm{t}+\sqrt{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }\right)>\mathrm{2},\forall\mathrm{x}\geqslant\mathrm{e} \\ $$$$\int_{\mathrm{2}} ^{\infty} \frac{\mathrm{ln}\left(\mathrm{t}+\sqrt{\mathrm{t}^{\mathrm{2}} +\mathrm{1}}\right)}{\mathrm{t}}\geqslant\int_{\mathrm{2}} ^{\infty} \frac{\mathrm{2}}{\mathrm{t}}\mathrm{dt}=\infty\:\mathrm{integral}\:\mathrm{didnt}\:\mathrm{cv} \\ $$
