
Question Number 216907 by MrGaster last updated on 24/Feb/25
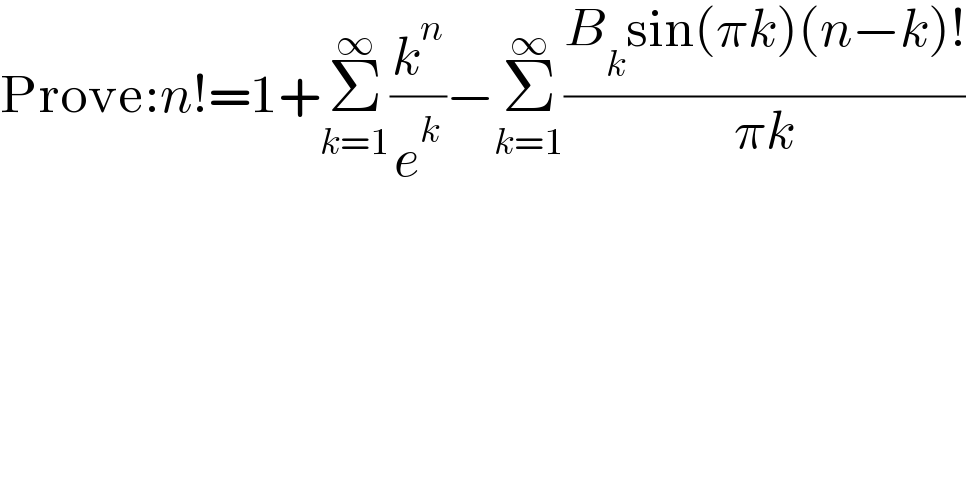
$$\mathrm{Prove}:{n}!=\mathrm{1}+\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{k}^{{n}} }{{e}^{{k}} }−\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{B}_{{k}} \mathrm{sin}\left(\pi{k}\right)\left({n}−{k}\right)!}{\pi{k}} \\ $$
Answered by MrGaster last updated on 13/Mar/25
![Let f(x)=(x/(e^x −1))&^⇔ (x/(e^x −1))=Σ_(k=0) ^∞ (B_k /(k!))x^k n!&n!=Γ(n+1)⇒Γ(n+1)=∫_0 ^∞ t^n e^(−t) dt Using the Euler-Maclaurinr ⇒Σ_(k=1) ^∞ f(k)=∫_1 ^∞ f(x)dx+((f(1))/2)+Σ_(k=1) ^m (B_(2k) /((2k)!))f^((2k+1)) (1)+R_m f(x)=(x^n /e^x )⇒Σ_(k=1) ^∞ (k^n /e^k )=∫_1 ^∞ (x^n /e^x )dx+(1/(2e))+R_m &^⇔ f(x)=((B_k sin(πk)(n−k)!)/(πk))⇒Σ_(n=1) ^∞ ((B_k sin(πk)(n−k)!)/(πk))=∫_1 ^∞ ((B_k sin(πx)(n−x)!)/(πx))dx+((B_1 sin(π)(n−1)!)/π)+Σ_(k=1) ^m (B_(2k) /((2k)!)) (d^(2k−1) /dx^(2k−1) )(((B_k sin(πx)(n−x)!)/(πx)))∣_(x=1) +R_m Combining these results⇒n!=1+Σ_(k=1) ^∞ (k^n /e^k )−Σ_(k=1) ^∞ ((B_k sin(πk)(n−k)!)/(πk)) [Q.E.D]](Q217430.png)
$$\mathrm{Let}\:{f}\left({x}\right)=\frac{{x}}{{e}^{{x}} −\mathrm{1}}\overset{\Leftrightarrow} {\&}\frac{{x}}{{e}^{{x}} −\mathrm{1}}=\underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{{B}_{{k}} }{{k}!}{x}^{{k}} \\ $$$${n}!\&{n}!=\Gamma\left({n}+\mathrm{1}\right)\Rightarrow\Gamma\left({n}+\mathrm{1}\right)=\int_{\mathrm{0}} ^{\infty} {t}^{{n}} {e}^{−{t}} {dt} \\ $$$$\mathrm{Using}\:\mathrm{the}\:\mathrm{Euler}-\mathrm{Maclaurinr} \\ $$$$\Rightarrow\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}{f}\left({k}\right)=\int_{\mathrm{1}} ^{\infty} {f}\left({x}\right){dx}+\frac{{f}\left(\mathrm{1}\right)}{\mathrm{2}}+\underset{{k}=\mathrm{1}} {\overset{{m}} {\sum}}\frac{{B}_{\mathrm{2}{k}} }{\left(\mathrm{2}{k}\right)!}{f}^{\left(\mathrm{2}{k}+\mathrm{1}\right)} \left(\mathrm{1}\right)+{R}_{{m}} \\ $$$${f}\left({x}\right)=\frac{{x}^{{n}} }{{e}^{{x}} }\Rightarrow\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{k}^{{n}} }{{e}^{{k}} }=\int_{\mathrm{1}} ^{\infty} \frac{{x}^{{n}} }{{e}^{{x}} }{dx}+\frac{\mathrm{1}}{\mathrm{2}{e}}+{R}_{{m}} \overset{\Leftrightarrow} {\&}{f}\left({x}\right)=\frac{{B}_{{k}} \mathrm{sin}\left(\pi{k}\right)\left({n}−{k}\right)!}{\pi{k}}\Rightarrow\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{B}_{{k}} \mathrm{sin}\left(\pi{k}\right)\left({n}−{k}\right)!}{\pi{k}}=\int_{\mathrm{1}} ^{\infty} \frac{{B}_{{k}} \mathrm{sin}\left(\pi{x}\right)\left({n}−{x}\right)!}{\pi{x}}{dx}+\frac{{B}_{\mathrm{1}} \mathrm{sin}\left(\pi\right)\left({n}−\mathrm{1}\right)!}{\pi}+\underset{{k}=\mathrm{1}} {\overset{{m}} {\sum}}\frac{{B}_{\mathrm{2}{k}} }{\left(\mathrm{2}{k}\right)!}\:\frac{{d}^{\mathrm{2}{k}−\mathrm{1}} }{{dx}^{\mathrm{2}{k}−\mathrm{1}} }\left(\frac{{B}_{{k}} \mathrm{sin}\left(\pi{x}\right)\left({n}−{x}\right)!}{\pi{x}}\right)\mid_{{x}=\mathrm{1}} +{R}_{{m}} \\ $$$$\mathrm{Combining}\:\mathrm{these}\:\mathrm{results}\Rightarrow{n}!=\mathrm{1}+\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{k}^{{n}} }{{e}^{{k}} }−\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{B}_{{k}} \mathrm{sin}\left(\pi{k}\right)\left({n}−{k}\right)!}{\pi{k}} \\ $$$$\left[\mathrm{Q}.\mathrm{E}.\mathrm{D}\right] \\ $$
