
Question Number 76037 by Crabby89p13 last updated on 22/Dec/19
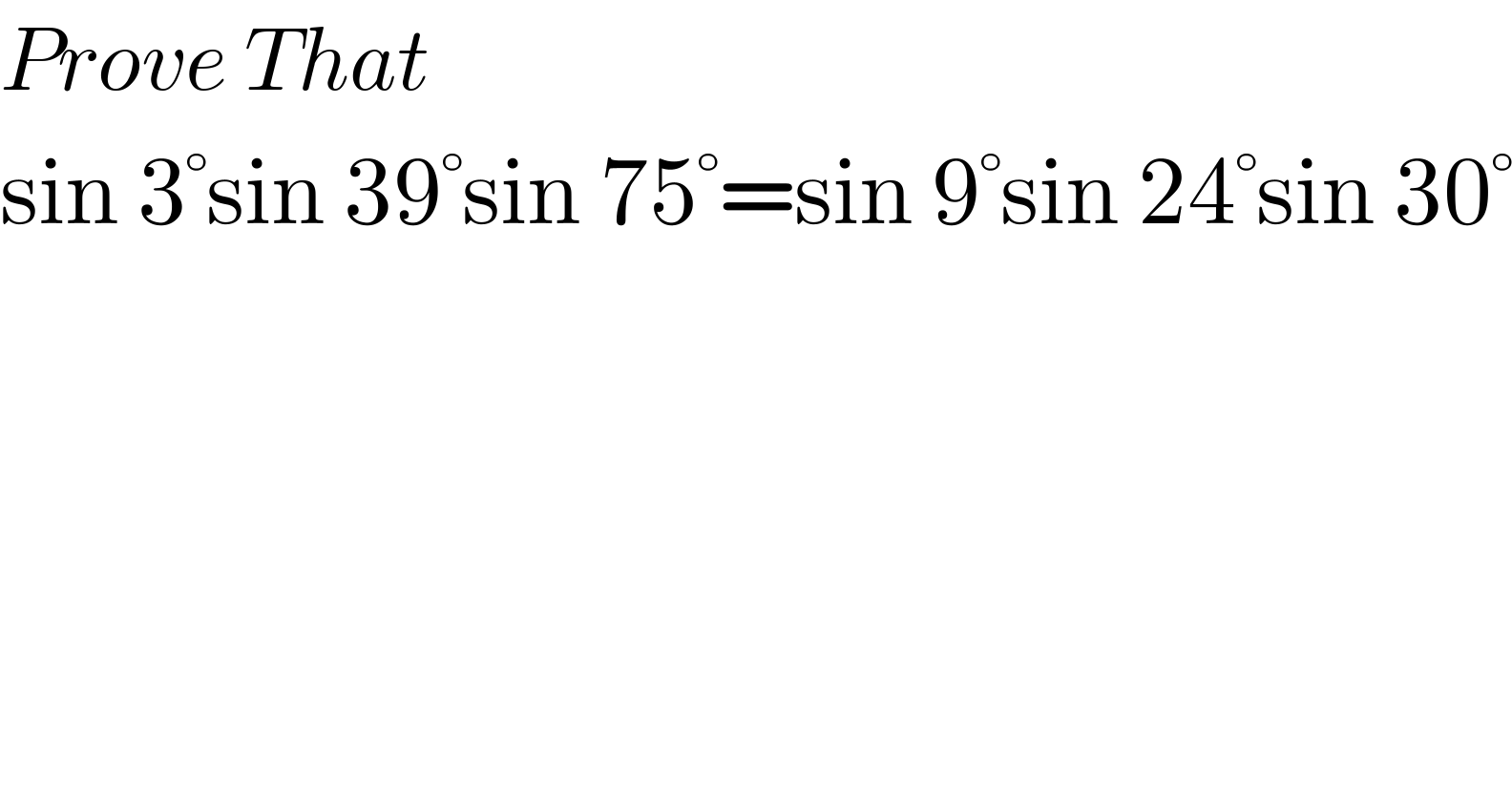
$${Prove}\:{That} \\ $$$$\mathrm{sin}\:\mathrm{3}°\mathrm{sin}\:\mathrm{39}°\mathrm{sin}\:\mathrm{75}°=\mathrm{sin}\:\mathrm{9}°\mathrm{sin}\:\mathrm{24}°\mathrm{sin}\:\mathrm{30}° \\ $$
Answered by MJS last updated on 23/Dec/19

$$\mathrm{sin}\:\mathrm{3}\:=\mathrm{sin}\:\left(\mathrm{75}−\mathrm{2}×\mathrm{36}\right)\:= \\ $$$$=\mathrm{2cos}^{\mathrm{2}} \:\mathrm{36}\:\mathrm{sin}\:\mathrm{75}\:−\mathrm{2sin}\:\mathrm{36}\:\mathrm{cos}\:\mathrm{36}\:\mathrm{cos}\:\mathrm{75}\:−\mathrm{sin}\:\mathrm{75}\:= \\ $$$$\mathrm{sin}\:\mathrm{39}\:=\mathrm{sin}\:\left(\mathrm{75}−\mathrm{36}\right)\:= \\ $$$$=\mathrm{cos}\:\mathrm{36}\:\mathrm{sin}\:\mathrm{75}\:−\mathrm{sin}\:\mathrm{36}\:\mathrm{cos}\:\mathrm{75} \\ $$$$\mathrm{sin}\:\mathrm{9}\:=\mathrm{sin}\:\left(\mathrm{45}−\mathrm{36}\right)\:= \\ $$$$=\mathrm{cos}\:\mathrm{36}\:\mathrm{sin}\:\mathrm{45}\:−\mathrm{sin}\:\mathrm{36}\:\mathrm{cos}\:\mathrm{45} \\ $$$$\mathrm{sin}\:\mathrm{24}\:=\mathrm{sin}\:\left(\mathrm{60}−\mathrm{36}\right)\:= \\ $$$$=\mathrm{cos}\:\mathrm{36}\:\mathrm{sin}\:\mathrm{60}\:−\mathrm{sin}\:\mathrm{36}\:\mathrm{cos}\:\mathrm{60} \\ $$$$\mathrm{let}\:\mathrm{sin}\:\mathrm{36}\:={u}\wedge\mathrm{cos}\:\mathrm{36}\:={v} \\ $$$$\mathrm{sin}\:\mathrm{75}\:=\frac{\sqrt{\mathrm{6}}+\sqrt{\mathrm{2}}}{\mathrm{4}};\:\mathrm{cos}\:\mathrm{75}\:=\frac{\sqrt{\mathrm{6}}−\sqrt{\mathrm{2}}}{\mathrm{4}} \\ $$$$\mathrm{sin}\:\mathrm{45}\:=\mathrm{cos}\:\mathrm{45}\:=\sqrt{\mathrm{2}} \\ $$$$\mathrm{sin}\:\mathrm{60}\:=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}};\:\mathrm{cos}\:\mathrm{60}\:=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{the}\:\mathrm{equation}\:\mathrm{now}\:\mathrm{is} \\ $$$$\frac{\mathrm{3}\sqrt{\mathrm{6}}+\mathrm{5}\sqrt{\mathrm{2}}}{\mathrm{8}}{v}^{\mathrm{3}} −\frac{\sqrt{\mathrm{6}}+\sqrt{\mathrm{2}}}{\mathrm{4}}{uv}^{\mathrm{2}} +\frac{\sqrt{\mathrm{6}}−\sqrt{\mathrm{2}}}{\mathrm{8}}{u}^{\mathrm{2}} {v}−\frac{\mathrm{3}\sqrt{\mathrm{6}}+\mathrm{5}\sqrt{\mathrm{2}}}{\mathrm{16}}{v}+\frac{\sqrt{\mathrm{6}}+\sqrt{\mathrm{2}}}{\mathrm{16}}{u}= \\ $$$$=\frac{\sqrt{\mathrm{6}}−\sqrt{\mathrm{2}}}{\mathrm{8}}{v}^{\mathrm{2}} −\frac{\sqrt{\mathrm{6}}+\sqrt{\mathrm{2}}}{\mathrm{8}}{uv}+\frac{\sqrt{\mathrm{2}}}{\mathrm{8}} \\ $$$$\mathrm{now}\:\mathrm{I}\:\mathrm{tried}\:\mathrm{a}\:\mathrm{while}... \\ $$$$\mathrm{let}\:{u}^{\mathrm{2}} =\mathrm{1}−{v}^{\mathrm{2}} \\ $$$$\Rightarrow \\ $$$$\frac{\sqrt{\mathrm{6}}+\mathrm{3}\sqrt{\mathrm{2}}}{\mathrm{4}}{v}^{\mathrm{3}} −\left(\frac{\sqrt{\mathrm{6}}+\sqrt{\mathrm{2}}}{\mathrm{4}}{u}+\frac{\sqrt{\mathrm{6}}−\sqrt{\mathrm{2}}}{\mathrm{8}}\right){v}^{\mathrm{2}} +\left(\frac{\sqrt{\mathrm{6}}+\sqrt{\mathrm{2}}}{\mathrm{8}}{u}−\frac{\sqrt{\mathrm{6}}+\mathrm{7}\sqrt{\mathrm{3}}}{\mathrm{16}}\right){v}+\frac{\sqrt{\mathrm{6}}+\sqrt{\mathrm{2}}}{\mathrm{16}}{u}+\frac{\sqrt{\mathrm{2}}}{\mathrm{8}}=\mathrm{0} \\ $$$$\mathrm{but}\:\mathrm{we}\:\mathrm{can}\:\mathrm{solve}\:\mathrm{this}\:\mathrm{for}\:{u} \\ $$$${u}=\sqrt{\mathrm{3}}{v}−\mathrm{1}+\sqrt{\mathrm{3}}\:\Leftrightarrow\:{v}_{\mathrm{1}} =\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}\left({u}+\mathrm{1}−\sqrt{\mathrm{3}}\right) \\ $$$$\Rightarrow \\ $$$$\left({v}−\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}\left({u}+\mathrm{1}−\sqrt{\mathrm{3}}\right)\right)\left({v}^{\mathrm{2}} −\frac{{v}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{4}}\right)=\mathrm{0} \\ $$$$\Rightarrow\:{v}_{\mathrm{2}} =\frac{\mathrm{1}−\sqrt{\mathrm{5}}}{\mathrm{4}};\:{v}_{\mathrm{3}} =\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{4}} \\ $$$$\mathrm{but}\:{v}=\mathrm{cos}\:\mathrm{36}\:=\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{4}} \\ $$$$\mathrm{proved} \\ $$
