
Question Number 176279 by CrispyXYZ last updated on 15/Sep/22

$$\mathrm{Proof}\:\mathrm{that}\:: \\ $$$$\nexists{n}\in\mathbb{Z},\:{n}^{\mathrm{2}} +\mathrm{1}\equiv\mathrm{0}\left(\mathrm{mod}\:\mathrm{4}\right) \\ $$
Answered by mahdipoor last updated on 15/Sep/22
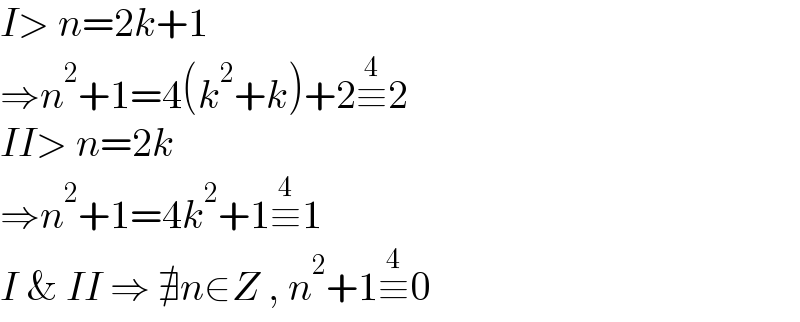
$${I}>\:{n}=\mathrm{2}{k}+\mathrm{1}\: \\ $$$$\Rightarrow{n}^{\mathrm{2}} +\mathrm{1}=\mathrm{4}\left({k}^{\mathrm{2}} +{k}\right)+\mathrm{2}\overset{\mathrm{4}} {\equiv}\mathrm{2}\:\: \\ $$$${II}>\:{n}=\mathrm{2}{k} \\ $$$$\Rightarrow{n}^{\mathrm{2}} +\mathrm{1}=\mathrm{4}{k}^{\mathrm{2}} +\mathrm{1}\overset{\mathrm{4}} {\equiv}\mathrm{1} \\ $$$${I}\:\&\:{II}\:\Rightarrow\:\nexists{n}\in{Z}\:,\:{n}^{\mathrm{2}} +\mathrm{1}\overset{\mathrm{4}} {\equiv}\mathrm{0} \\ $$
