Question and Answers Forum

All Questions      Topic List

Number Theory Questions

Previous in All Question      Next in All Question      

Previous in Number Theory      Next in Number Theory      

Question Number 112999 by Aina Samuel Temidayo last updated on 10/Sep/20

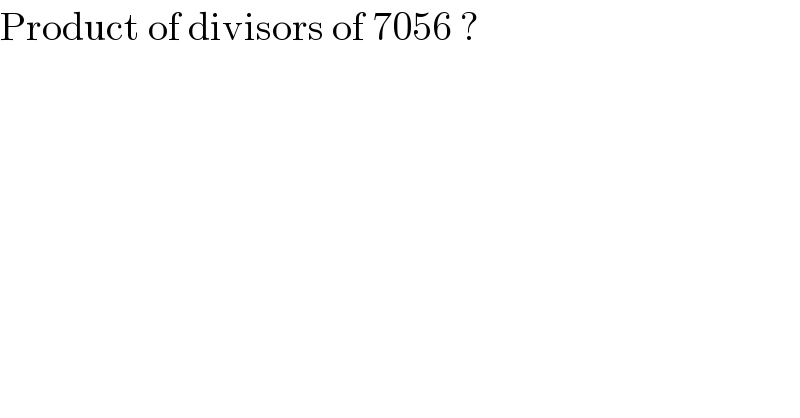
Product of divisors of 7056 ?

$$\mathrm{Product}\:\mathrm{of}\:\mathrm{divisors}\:\mathrm{of}\:\mathrm{7056}\:? \\ $$

Answered by mr W last updated on 10/Sep/20

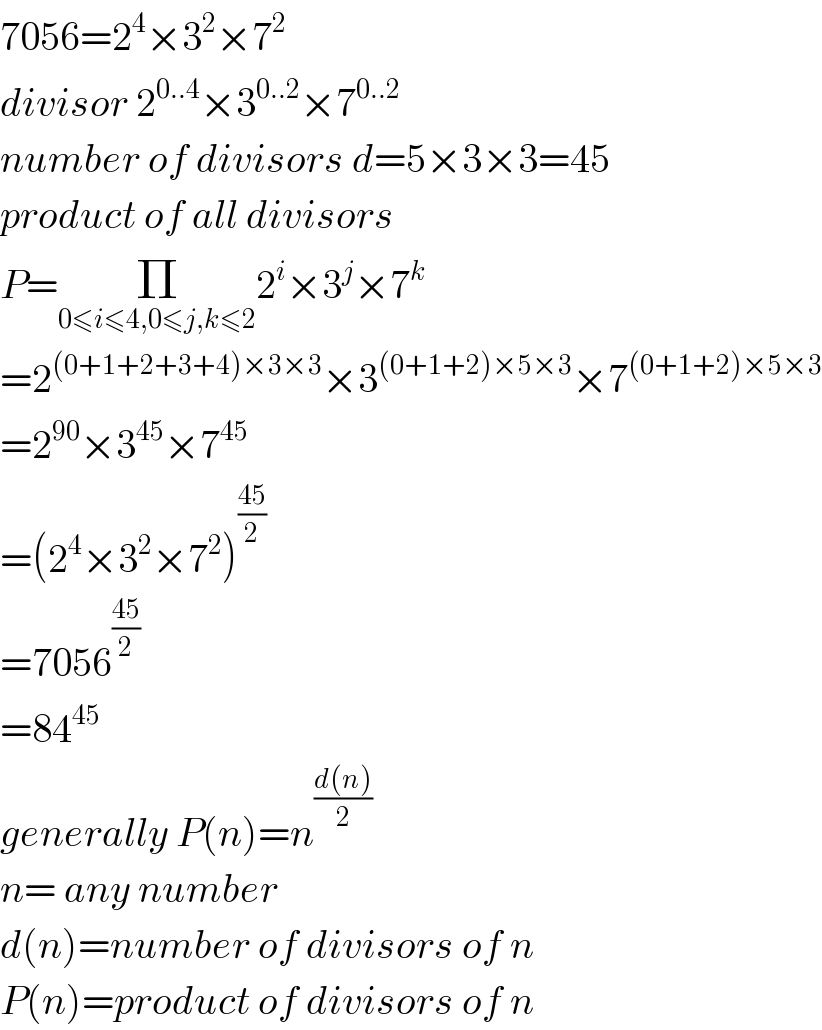
7056=2^4 ×3^2 ×7^2 divisor 2^(0..4) ×3^(0..2) ×7^(0..2) number of divisors d=5×3×3=45 product of all divisors P=Π_(0≤i≤4,0≤j,k≤2) 2^i ×3^j ×7^k =2^((0+1+2+3+4)×3×3) ×3^((0+1+2)×5×3) ×7^((0+1+2)×5×3) =2^(90) ×3^(45) ×7^(45) =(2^4 ×3^2 ×7^2 )^((45)/2) =7056^((45)/2) =84^(45) generally P(n)=n^((d(n))/2) n= any number d(n)=number of divisors of n P(n)=product of divisors of n

$$\mathrm{7056}=\mathrm{2}^{\mathrm{4}} ×\mathrm{3}^{\mathrm{2}} ×\mathrm{7}^{\mathrm{2}} \\ $$$${divisor}\:\mathrm{2}^{\mathrm{0}..\mathrm{4}} ×\mathrm{3}^{\mathrm{0}..\mathrm{2}} ×\mathrm{7}^{\mathrm{0}..\mathrm{2}} \\ $$$${number}\:{of}\:{divisors}\:{d}=\mathrm{5}×\mathrm{3}×\mathrm{3}=\mathrm{45} \\ $$$${product}\:{of}\:{all}\:{divisors} \\ $$$${P}=\underset{\mathrm{0}\leqslant{i}\leqslant\mathrm{4},\mathrm{0}\leqslant{j},{k}\leqslant\mathrm{2}} {\prod}\mathrm{2}^{{i}} ×\mathrm{3}^{{j}} ×\mathrm{7}^{{k}} \\ $$$$=\mathrm{2}^{\left(\mathrm{0}+\mathrm{1}+\mathrm{2}+\mathrm{3}+\mathrm{4}\right)×\mathrm{3}×\mathrm{3}} ×\mathrm{3}^{\left(\mathrm{0}+\mathrm{1}+\mathrm{2}\right)×\mathrm{5}×\mathrm{3}} ×\mathrm{7}^{\left(\mathrm{0}+\mathrm{1}+\mathrm{2}\right)×\mathrm{5}×\mathrm{3}} \\ $$$$=\mathrm{2}^{\mathrm{90}} ×\mathrm{3}^{\mathrm{45}} ×\mathrm{7}^{\mathrm{45}} \\ $$$$=\left(\mathrm{2}^{\mathrm{4}} ×\mathrm{3}^{\mathrm{2}} ×\mathrm{7}^{\mathrm{2}} \right)^{\frac{\mathrm{45}}{\mathrm{2}}} \\ $$$$=\mathrm{7056}^{\frac{\mathrm{45}}{\mathrm{2}}} \\ $$$$=\mathrm{84}^{\mathrm{45}} \\ $$$${generally}\:{P}\left({n}\right)={n}^{\frac{{d}\left({n}\right)}{\mathrm{2}}} \\ $$$${n}=\:{any}\:{number} \\ $$$${d}\left({n}\right)={number}\:{of}\:{divisors}\:{of}\:{n} \\ $$$${P}\left({n}\right)={product}\:{of}\:{divisors}\:{of}\:{n} \\ $$

Commented by Aina Samuel Temidayo last updated on 10/Sep/20

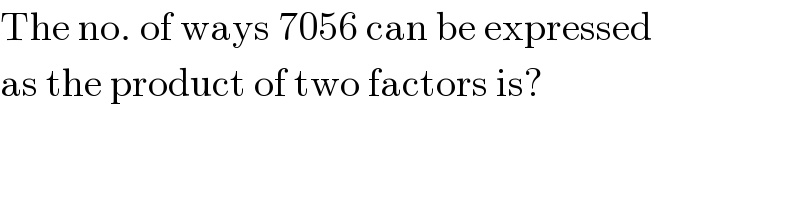
The no. of ways 7056 can be expressed as the product of two factors is?

$$\mathrm{The}\:\mathrm{no}.\:\mathrm{of}\:\mathrm{ways}\:\mathrm{7056}\:\mathrm{can}\:\mathrm{be}\:\mathrm{expressed} \\ $$$$\mathrm{as}\:\mathrm{the}\:\mathrm{product}\:\mathrm{of}\:\mathrm{two}\:\mathrm{factors}\:\mathrm{is}? \\ $$

Commented by mr W last updated on 10/Sep/20

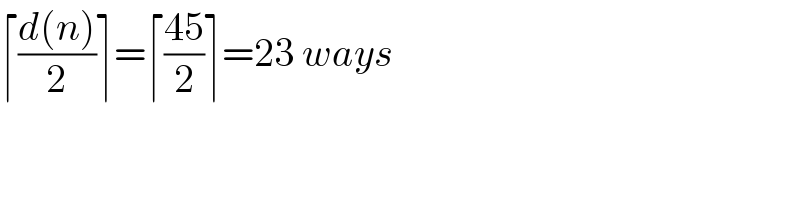
⌈((d(n))/2)⌉=⌈((45)/2)⌉=23 ways

$$\lceil\frac{{d}\left({n}\right)}{\mathrm{2}}\rceil=\lceil\frac{\mathrm{45}}{\mathrm{2}}\rceil=\mathrm{23}\:{ways} \\ $$

Commented by Aina Samuel Temidayo last updated on 10/Sep/20

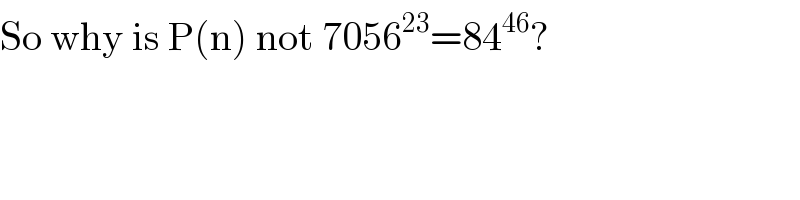
So why is P(n) not 7056^(23) =84^(46) ?

$$\mathrm{So}\:\mathrm{why}\:\mathrm{is}\:\mathrm{P}\left(\mathrm{n}\right)\:\mathrm{not}\:\mathrm{7056}^{\mathrm{23}} =\mathrm{84}^{\mathrm{46}} ? \\ $$

Commented by mr W last updated on 11/Sep/20

say n=16, its divisors are 1, 2, 4, 8, 16 16=1×8, 2×16, 4×4 ⇒3 ways (to be exact this is not correct, since we use the factor 4 twice) P=1×2×4×8×16=1×16×2×8×4 =16×16×4≠16×16×16

$${say}\:{n}=\mathrm{16},\:{its}\:{divisors}\:{are} \\ $$$$\mathrm{1},\:\mathrm{2},\:\mathrm{4},\:\mathrm{8},\:\mathrm{16} \\ $$$$\mathrm{16}=\mathrm{1}×\mathrm{8},\:\mathrm{2}×\mathrm{16},\:\mathrm{4}×\mathrm{4}\:\Rightarrow\mathrm{3}\:{ways} \\ $$$$\left({to}\:{be}\:{exact}\:{this}\:{is}\:{not}\:{correct},\:{since}\right. \\ $$$$\left.{we}\:{use}\:{the}\:{factor}\:\mathrm{4}\:{twice}\right) \\ $$$$ \\ $$$${P}=\mathrm{1}×\mathrm{2}×\mathrm{4}×\mathrm{8}×\mathrm{16}=\mathrm{1}×\mathrm{16}×\mathrm{2}×\mathrm{8}×\mathrm{4} \\ $$$$=\mathrm{16}×\mathrm{16}×\mathrm{4}\neq\mathrm{16}×\mathrm{16}×\mathrm{16} \\ $$

Commented by Aina Samuel Temidayo last updated on 11/Sep/20

Ok. Thanks.

$$\mathrm{Ok}.\:\mathrm{Thanks}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com