Question Number 134591 by bobhans last updated on 05/Mar/21

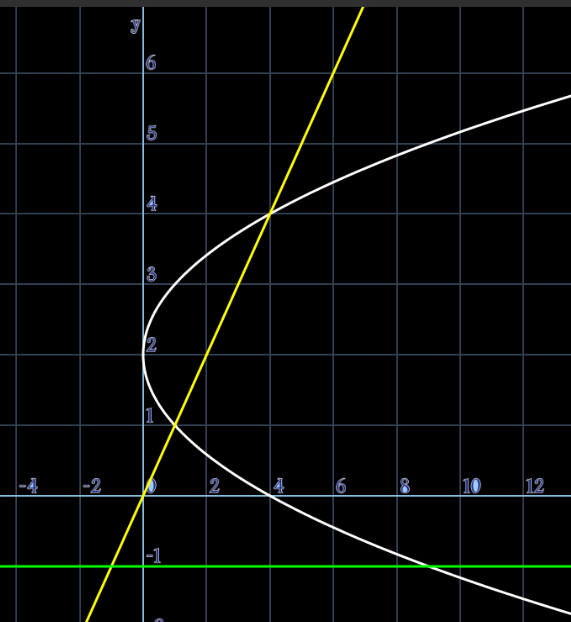
$$\mathrm{Precalculus} \\ $$ What is the volume of the solid obtained by rotating the region bounded by x = (y−2)^2 and y = x about the line y = −1 by the method of cylindrical shells?\\n
Answered by EDWIN88 last updated on 05/Mar/21
![Vol=2π∫_1 ^( 4) (y+1)(y−(y−2)^2 )dy V=2π∫_1 ^( 4) (y+1)(5y−y^2 −4)dy V=2π∫_1 ^( 4) (4y^2 +y−y^3 −4)dy V=2π [ ((4y^3 )/3)+(y^2 /2)−(y^4 /4)−4y ]_1 ^4 V=2π [((4(63))/3)+((15)/2)−((255)/4)−12 ] V=2π [ 72−((225)/4) ]= ((63π)/2)](Q134592.png)
$$\mathrm{Vol}=\mathrm{2}\pi\int_{\mathrm{1}} ^{\:\mathrm{4}} \left(\mathrm{y}+\mathrm{1}\right)\left(\mathrm{y}−\left(\mathrm{y}−\mathrm{2}\right)^{\mathrm{2}} \right)\mathrm{dy} \\ $$ $$\mathrm{V}=\mathrm{2}\pi\int_{\mathrm{1}} ^{\:\mathrm{4}} \left(\mathrm{y}+\mathrm{1}\right)\left(\mathrm{5y}−\mathrm{y}^{\mathrm{2}} −\mathrm{4}\right)\mathrm{dy} \\ $$ $$\mathrm{V}=\mathrm{2}\pi\int_{\mathrm{1}} ^{\:\mathrm{4}} \left(\mathrm{4y}^{\mathrm{2}} +\mathrm{y}−\mathrm{y}^{\mathrm{3}} −\mathrm{4}\right)\mathrm{dy} \\ $$ $$\mathrm{V}=\mathrm{2}\pi\:\left[\:\frac{\mathrm{4y}^{\mathrm{3}} }{\mathrm{3}}+\frac{\mathrm{y}^{\mathrm{2}} }{\mathrm{2}}−\frac{\mathrm{y}^{\mathrm{4}} }{\mathrm{4}}−\mathrm{4y}\:\right]_{\mathrm{1}} ^{\mathrm{4}} \\ $$ $$\mathrm{V}=\mathrm{2}\pi\:\left[\frac{\mathrm{4}\left(\mathrm{63}\right)}{\mathrm{3}}+\frac{\mathrm{15}}{\mathrm{2}}−\frac{\mathrm{255}}{\mathrm{4}}−\mathrm{12}\:\right] \\ $$ $$\mathrm{V}=\mathrm{2}\pi\:\left[\:\mathrm{72}−\frac{\mathrm{225}}{\mathrm{4}}\:\right]=\:\frac{\mathrm{63}\pi}{\mathrm{2}} \\ $$
Commented bybobhans last updated on 05/Mar/21