
Question Number 124537 by nimnim last updated on 04/Dec/20
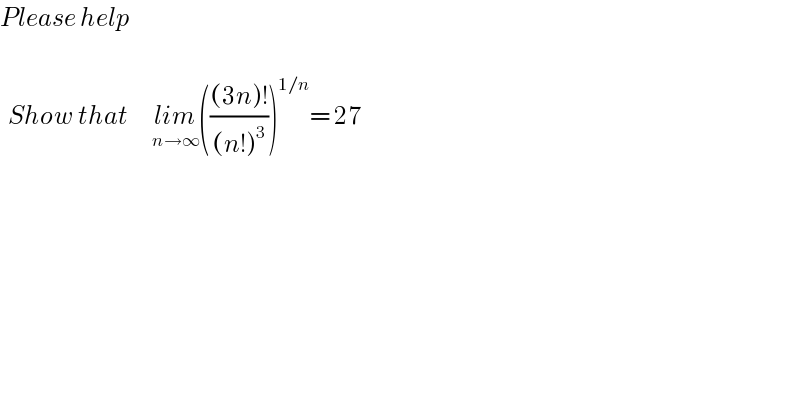
$${Please}\:{help} \\ $$$$ \\ $$$$\:\:{Show}\:{that}\:\:\:\:\:\:\underset{{n}\rightarrow\infty} {{lim}}\left(\frac{\left(\mathrm{3}{n}\right)!}{\left({n}!\right)^{\mathrm{3}} }\right)^{\mathrm{1}/{n}} =\:\mathrm{27} \\ $$
Answered by Dwaipayan Shikari last updated on 04/Dec/20
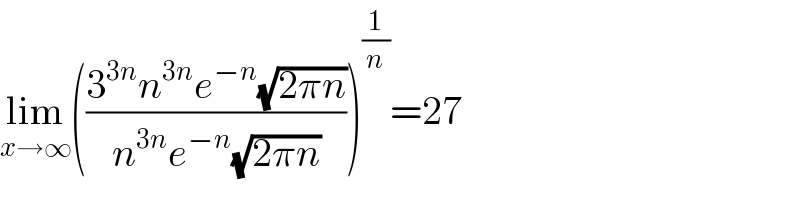
$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\left(\frac{\mathrm{3}^{\mathrm{3}{n}} {n}^{\mathrm{3}{n}} {e}^{−{n}} \sqrt{\mathrm{2}\pi{n}}}{{n}^{\mathrm{3}{n}} {e}^{−{n}} \sqrt{\mathrm{2}\pi{n}}}\right)^{\frac{\mathrm{1}}{{n}}} =\mathrm{27}\:\:\:\:\:\: \\ $$
Commented by mnjuly1970 last updated on 04/Dec/20

$${good}\:{very}\:{good} \\ $$$${stirling}\:{approximation}... \\ $$
Commented by mohammad17 last updated on 05/Dec/20

$${how}\:{this}\:? \\ $$
