
Permutation and CombinationQuestion and Answers: Page 3
Question Number 202374 Answers: 1 Comments: 2
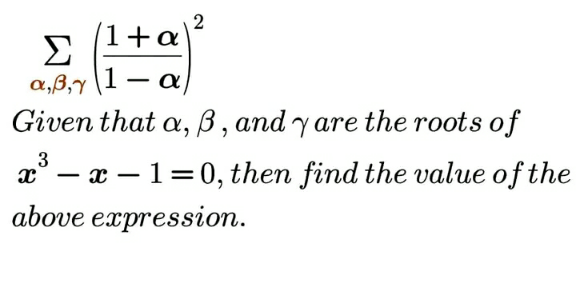
Question Number 202257 Answers: 0 Comments: 2

Question Number 201839 Answers: 0 Comments: 1

Question Number 200051 Answers: 2 Comments: 2
Question Number 199337 Answers: 1 Comments: 0

Question Number 199333 Answers: 2 Comments: 0
Question Number 199270 Answers: 2 Comments: 4

Question Number 199353 Answers: 0 Comments: 4
Question Number 199054 Answers: 2 Comments: 0
Question Number 199031 Answers: 1 Comments: 0

Question Number 198851 Answers: 1 Comments: 12
Question Number 198809 Answers: 2 Comments: 0
Question Number 198576 Answers: 1 Comments: 10
Question Number 198242 Answers: 1 Comments: 3
Question Number 198231 Answers: 1 Comments: 0
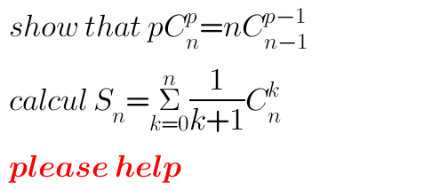
Question Number 198022 Answers: 1 Comments: 0
Question Number 197564 Answers: 1 Comments: 4
Question Number 197311 Answers: 1 Comments: 0
Question Number 197589 Answers: 1 Comments: 0
Question Number 198283 Answers: 1 Comments: 1
Question Number 196322 Answers: 1 Comments: 0
Question Number 196143 Answers: 2 Comments: 0
Question Number 195964 Answers: 1 Comments: 0
Question Number 195666 Answers: 1 Comments: 2
Question Number 195672 Answers: 2 Comments: 0
Question Number 195538 Answers: 1 Comments: 7
