Question and Answers Forum

Permutation and CombinationQuestion and Answers: Page 25

Question Number 11425 Answers: 1 Comments: 0

Question Number 11384 Answers: 1 Comments: 0

Out of 5 accountants and 7 bankers, a committee consisting of 2 accountants and 3 bankers is to be formed. In how many ways can this be done if (a) Any acountant and any bankers must be included (b) One particular banker must be included (c) 2 accountant cannot be in the committee

$$\mathrm{Out}\:\mathrm{of}\:\mathrm{5}\:\mathrm{accountants}\:\mathrm{and}\:\mathrm{7}\:\mathrm{bankers},\:\mathrm{a}\:\mathrm{committee}\:\mathrm{consisting}\:\mathrm{of}\: \\ $$$$\mathrm{2}\:\mathrm{accountants}\:\mathrm{and}\:\mathrm{3}\:\mathrm{bankers}\:\mathrm{is}\:\mathrm{to}\:\mathrm{be}\:\mathrm{formed}.\:\mathrm{In}\:\mathrm{how}\:\mathrm{many}\:\mathrm{ways}\:\mathrm{can}\:\mathrm{this} \\ $$$$\mathrm{be}\:\mathrm{done}\:\mathrm{if} \\ $$$$\left(\mathrm{a}\right)\:\mathrm{Any}\:\mathrm{acountant}\:\mathrm{and}\:\mathrm{any}\:\mathrm{bankers}\:\mathrm{must}\:\mathrm{be}\:\mathrm{included} \\ $$$$\left(\mathrm{b}\right)\:\mathrm{One}\:\mathrm{particular}\:\mathrm{banker}\:\mathrm{must}\:\mathrm{be}\:\mathrm{included} \\ $$$$\left(\mathrm{c}\right)\:\mathrm{2}\:\mathrm{accountant}\:\mathrm{cannot}\:\mathrm{be}\:\mathrm{in}\:\mathrm{the}\:\mathrm{committee} \\ $$

Question Number 11382 Answers: 0 Comments: 2

In how many ways can 24 different articles be divided into groups of 12, 8 and 4 articles respectively

$$\mathrm{In}\:\mathrm{how}\:\mathrm{many}\:\mathrm{ways}\:\mathrm{can}\:\mathrm{24}\:\mathrm{different}\:\mathrm{articles}\:\mathrm{be}\:\mathrm{divided}\:\mathrm{into}\:\mathrm{groups}\:\mathrm{of} \\ $$$$\mathrm{12},\:\mathrm{8}\:\mathrm{and}\:\mathrm{4}\:\mathrm{articles}\:\mathrm{respectively} \\ $$

Question Number 10029 Answers: 0 Comments: 1

The first 3 runners in 100m race were clocked 9.5s, 10s, 10.5s respectively. How far is the first from the third runners when the first runner reached the finished line.

$$\mathrm{The}\:\mathrm{first}\:\mathrm{3}\:\mathrm{runners}\:\mathrm{in}\:\mathrm{100m}\:\mathrm{race}\:\mathrm{were}\:\mathrm{clocked} \\ $$$$\mathrm{9}.\mathrm{5s},\:\mathrm{10s},\:\mathrm{10}.\mathrm{5s}\:\mathrm{respectively}.\:\mathrm{How}\:\mathrm{far}\:\mathrm{is}\:\mathrm{the}\: \\ $$$$\mathrm{first}\:\mathrm{from}\:\mathrm{the}\:\mathrm{third}\:\mathrm{runners}\:\mathrm{when}\:\mathrm{the}\:\mathrm{first}\: \\ $$$$\mathrm{runner}\:\mathrm{reached}\:\mathrm{the}\:\mathrm{finished}\:\mathrm{line}. \\ $$

Question Number 9747 Answers: 1 Comments: 0

Find the coefficient of the term independent of x in the expansion of (((x + 1)/(x^(2/3) − x^(1/3) + 1)) − ((x − 1)/(x − x^(1/2) )))^(10)

$$\mathrm{Find}\:\mathrm{the}\:\mathrm{coefficient}\:\mathrm{of}\:\mathrm{the}\:\mathrm{term}\:\mathrm{independent} \\ $$$$\mathrm{of}\:\mathrm{x}\:\mathrm{in}\:\mathrm{the}\:\mathrm{expansion}\:\mathrm{of} \\ $$$$\left(\frac{\mathrm{x}\:+\:\mathrm{1}}{\mathrm{x}^{\mathrm{2}/\mathrm{3}} \:−\:\mathrm{x}^{\mathrm{1}/\mathrm{3}} \:+\:\mathrm{1}}\:−\:\frac{\mathrm{x}\:−\:\mathrm{1}}{\mathrm{x}\:−\:\mathrm{x}^{\mathrm{1}/\mathrm{2}} }\right)^{\mathrm{10}} \\ $$

Question Number 9573 Answers: 0 Comments: 1

If n is positive integer prove that the cofficient of x^(2 ) and x^3 in the expansion of (x^2 +2x+2)^n are 2^(n−1) .n^2 and 2^(n−1) n(n−1)(1/3).

$${If}\:{n}\:{is}\:{positive}\:{integer}\:{prove}\:{that}\: \\ $$$${the}\:{cofficient}\:{of}\:{x}^{\mathrm{2}\:} {and}\:{x}^{\mathrm{3}} \:{in}\:{the}\: \\ $$$${expansion}\:{of}\:\left({x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{2}\right)^{{n}} \:{are}\:\mathrm{2}^{{n}−\mathrm{1}} .{n}^{\mathrm{2}} \\ $$$${and}\:\mathrm{2}^{{n}−\mathrm{1}} {n}\left({n}−\mathrm{1}\right)\frac{\mathrm{1}}{\mathrm{3}}. \\ $$

Question Number 9569 Answers: 0 Comments: 0

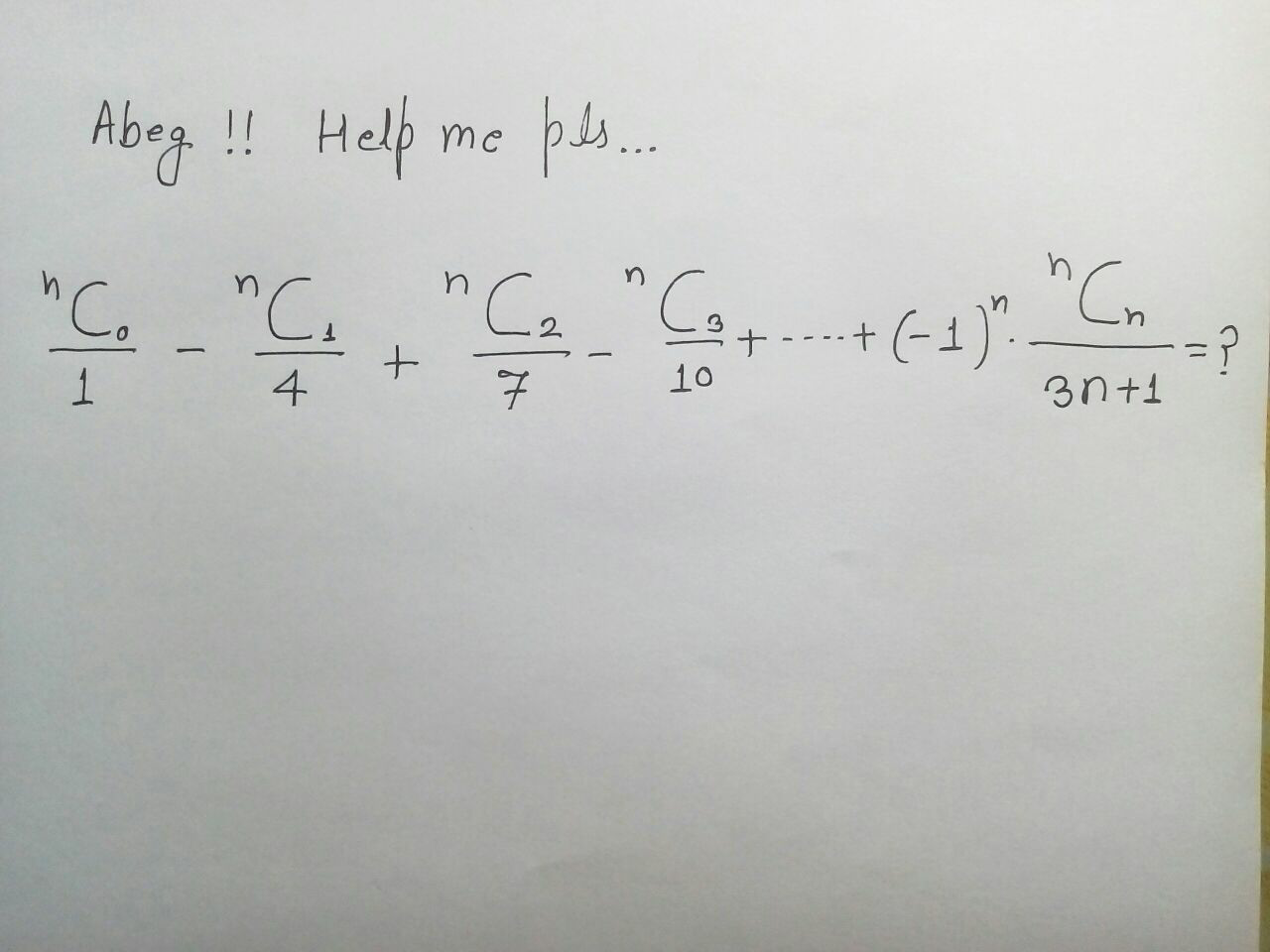
Question Number 9495 Answers: 0 Comments: 0

Question Number 9474 Answers: 0 Comments: 0

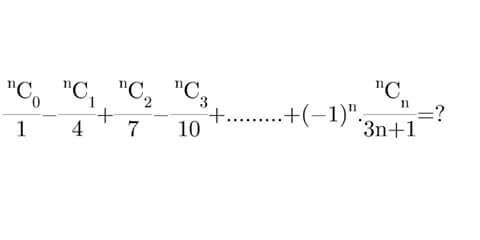
Question Number 6090 Answers: 1 Comments: 0

Question Number 5989 Answers: 1 Comments: 0

Evaluate 10 ×12 × 14 × 16 × 18 × 20 into factorial form

$${Evaluate}\:\:\:\mathrm{10}\:×\mathrm{12}\:×\:\mathrm{14}\:×\:\mathrm{16}\:×\:\mathrm{18}\:×\:\mathrm{20}\:\:{into}\:{factorial}\:{form} \\ $$

Question Number 5444 Answers: 2 Comments: 0

$$\mathrm{8} \\ $$

Question Number 5283 Answers: 1 Comments: 1

If 8C4 = 8Cn . find the value of n

$${If}\:\:\:\:\:\:\:\:\:\mathrm{8}{C}\mathrm{4}\:=\:\mathrm{8}{Cn}\:\:.\:\:{find}\:{the}\:{value}\:{of}\:{n} \\ $$$$ \\ $$

Question Number 5280 Answers: 1 Comments: 0

A delegation of 4 people is to be selected from 5 women and 6 men. Find the number of possible delegations if (a) there are no restrictions, (b) there is at least 1 woman, (c) there are at least 2 women. One of the men cannot get along with one of the women. Find the number of delegations which include this particular man or woman, but not both.

$$\mathrm{A}\:\mathrm{delegation}\:\mathrm{of}\:\mathrm{4}\:\mathrm{people}\:\mathrm{is}\:\mathrm{to}\:\mathrm{be} \\ $$$$\mathrm{selected}\:\mathrm{from}\:\mathrm{5}\:\mathrm{women}\:\mathrm{and}\:\mathrm{6}\:\:\mathrm{men}. \\ $$$$\mathrm{Find}\:\mathrm{the}\:\mathrm{number}\:\mathrm{of}\:\mathrm{possible}\:\mathrm{delegations}\:\mathrm{if} \\ $$$$\left(\boldsymbol{\mathrm{a}}\right)\:\mathrm{there}\:\mathrm{are}\:\mathrm{no}\:\mathrm{restrictions}, \\ $$$$\:\left(\boldsymbol{\mathrm{b}}\right)\:\mathrm{there}\:\mathrm{is}\:\mathrm{at}\:\mathrm{least}\:\mathrm{1}\:\mathrm{woman}, \\ $$$$\left(\boldsymbol{\mathrm{c}}\right)\:\mathrm{there}\:\mathrm{are}\:\mathrm{at}\:\mathrm{least}\:\mathrm{2}\:\mathrm{women}. \\ $$$$\mathrm{One}\:\mathrm{of}\:\mathrm{the}\:\mathrm{men}\:\mathrm{cannot}\:\mathrm{get}\:\mathrm{along}\:\mathrm{with}\:\: \\ $$$$\mathrm{one}\:\mathrm{of}\:\mathrm{the}\:\mathrm{women}.\:\mathrm{Find}\:\mathrm{the}\:\mathrm{number}\:\mathrm{of} \\ $$$$\mathrm{delegations}\:\mathrm{which}\:\mathrm{include}\:\mathrm{this}\:\mathrm{particular}\: \\ $$$$\mathrm{man}\:\mathrm{or}\:\mathrm{woman},\:\mathrm{but}\:\mathrm{not}\:\mathrm{both}. \\ $$$$ \\ $$

Question Number 5275 Answers: 1 Comments: 0

Question Number 5254 Answers: 1 Comments: 1

Calculate the number of ways in which (a) 5 children can be divided into groups of 2 and 3 , (b) 9 children can be divided into groups of 5 and 4, Hence calculate the number of ways in which 9 children can be divided into groups of 2,3 and 4.

$$\mathrm{Calculate}\:\mathrm{the}\:\mathrm{number}\:\mathrm{of}\:\mathrm{ways}\:\mathrm{in}\:\mathrm{which} \\ $$$$\left(\boldsymbol{\mathrm{a}}\right)\:\mathrm{5}\:\mathrm{children}\:\mathrm{can}\:\mathrm{be}\:\mathrm{divided}\:\mathrm{into}\:\mathrm{groups} \\ $$$$\mathrm{of}\:\mathrm{2}\:\mathrm{and}\:\mathrm{3}\:, \\ $$$$\left(\boldsymbol{\mathrm{b}}\right)\:\mathrm{9}\:\mathrm{children}\:\mathrm{can}\:\mathrm{be}\:\mathrm{divided}\:\mathrm{into}\:\mathrm{groups} \\ $$$$\mathrm{of}\:\mathrm{5}\:\mathrm{and}\:\mathrm{4}, \\ $$$$\mathrm{Hence}\:\mathrm{calculate}\:\mathrm{the}\:\mathrm{number}\:\mathrm{of}\:\mathrm{ways}\:\mathrm{in} \\ $$$$\mathrm{which}\:\mathrm{9}\:\mathrm{children}\:\mathrm{can}\:\mathrm{be}\:\mathrm{divided}\:\mathrm{into} \\ $$$$\mathrm{groups}\:\mathrm{of}\:\mathrm{2},\mathrm{3}\:\mathrm{and}\:\mathrm{4}. \\ $$

Question Number 4164 Answers: 1 Comments: 2

Question Number 4105 Answers: 0 Comments: 2

How many distinct ways are there for a knight to reach from bottom left corner of chessboard to top right corner. (knight going from square a1 to h8).

$$\mathrm{How}\:\mathrm{many}\:\mathrm{distinct}\:\mathrm{ways}\:\mathrm{are}\:\mathrm{there}\:\mathrm{for} \\ $$$$\mathrm{a}\:\mathrm{knight}\:\mathrm{to}\:\mathrm{reach}\:\mathrm{from}\:\mathrm{bottom}\:\mathrm{left}\:\mathrm{corner}\:\mathrm{of} \\ $$$$\mathrm{chessboard}\:\mathrm{to}\:\mathrm{top}\:\mathrm{right}\:\mathrm{corner}. \\ $$$$\left(\mathrm{knight}\:\mathrm{going}\:\mathrm{from}\:\mathrm{square}\:\mathrm{a1}\:\mathrm{to}\:\mathrm{h8}\right). \\ $$

Question Number 4103 Answers: 0 Comments: 9

Prove that Σ_(m=1) ^n (((−1)^m ∙(2^m −1) ∙^n C_m )/m) =Σ_(m=1) ^n (((−1)^m )/m)

$$\mathrm{Prove}\:\mathrm{that} \\ $$$$\underset{{m}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\left(−\mathrm{1}\right)^{{m}} \:\centerdot\left(\mathrm{2}^{{m}} −\mathrm{1}\right)\:\centerdot\:^{{n}} {C}_{{m}} }{{m}}\:\:=\underset{{m}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\left(−\mathrm{1}\right)^{{m}} }{{m}} \\ $$

Question Number 3884 Answers: 1 Comments: 4

Prove that there are (((n+r−1)),((n−1)) ) ways of placing r identical objects in n compartments, where n>r.

$${Prove}\:{that}\:{there}\:{are}\:\begin{pmatrix}{{n}+{r}−\mathrm{1}}\\{{n}−\mathrm{1}}\end{pmatrix}\: \\ $$$${ways}\:{of}\:{placing}\:{r}\:{identical}\:{objects} \\ $$$${in}\:{n}\:{compartments},\:{where}\:{n}>{r}. \\ $$

Question Number 3881 Answers: 1 Comments: 4

Four integers are chosen at random from 0 to 9, inclusive. Find the probability that no more than 2 integers are the same.

$${Four}\:{integers}\:{are}\:{chosen}\:{at}\:{random} \\ $$$${from}\:\mathrm{0}\:{to}\:\mathrm{9},\:{inclusive}.\:{Find}\:{the} \\ $$$${probability}\:{that}\:{no}\:{more}\:{than} \\ $$$$\mathrm{2}\:{integers}\:{are}\:{the}\:{same}.\: \\ $$$$ \\ $$

Question Number 3274 Answers: 1 Comments: 0

I have 25 horses and I′d like to know which are the three fastest horses among them. I do not have a clock but I have a race track which can be used by 5 horses at a time. If each horse covers the distance of the track in the same time for every race it runs, find the least number of races that ought to be held in order to identify the three fastest horses.

$${I}\:{have}\:\mathrm{25}\:{horses}\:{and}\:{I}'{d}\:{like}\:{to} \\ $$$${know}\:{which}\:{are}\:{the}\:{three}\:{fastest} \\ $$$${horses}\:{among}\:{them}.\:{I}\:{do}\:{not}\:{have}\:{a} \\ $$$${clock}\:{but}\:{I}\:{have}\:{a}\:{race}\:{track}\:{which} \\ $$$${can}\:{be}\:{used}\:{by}\:\mathrm{5}\:{horses}\:{at}\:{a}\:{time}. \\ $$$${If}\:{each}\:{horse}\:{covers}\:{the}\:{distance} \\ $$$${of}\:{the}\:{track}\:{in}\:{the}\:{same}\:{time}\:{for} \\ $$$${every}\:{race}\:{it}\:{runs},\:{find}\:{the}\:{least} \\ $$$${number}\:{of}\:{races}\:{that}\:{ought}\:{to}\:{be} \\ $$$${held}\:{in}\:{order}\:{to}\:{identify}\:{the}\:{three} \\ $$$${fastest}\:{horses}.\: \\ $$$$ \\ $$

Question Number 3273 Answers: 3 Comments: 0

∗ ∗ ∗ ∗ One can only move to the ∗ ∗ ∗ ∗ right or downwards on the ∗ ∗ ∗ ∗ 4 by 6 point lattice shown. ∗ ∗ ∗ ∗ How many paths from ∗ to ∗ ∗ ∗ ∗ ∗ are there? ∗ ∗ ∗ ∗

$$\ast\:\:\ast\:\:\ast\:\:\ast\:\:\:\:{One}\:{can}\:{only}\:{move}\:{to}\:{the} \\ $$$$\ast\:\:\ast\:\:\ast\:\:\ast\:\:\:\:{right}\:{or}\:{downwards}\:{on}\:{the} \\ $$$$\ast\:\:\ast\:\:\ast\:\:\ast\:\:\:\:\mathrm{4}\:{by}\:\mathrm{6}\:{point}\:{lattice}\:{shown}. \\ $$$$\ast\:\:\ast\:\:\ast\:\:\ast\:\:\:\:{How}\:{many}\:{paths}\:{from}\:\ast\:{to} \\ $$$$\ast\:\:\ast\:\:\ast\:\:\ast\:\:\:\:\:\:\ast\:{are}\:{there}?\: \\ $$$$\ast\:\:\ast\:\:\ast\:\:\ast \\ $$$$ \\ $$

Question Number 3216 Answers: 1 Comments: 0

You have unlimited number of 1kg, 5kg 10kg and 25 kg weights. In how many ways you can create a total of 43kg. For example 43×1 5×8+3×2 etc.

$$\mathrm{You}\:\mathrm{have}\:\mathrm{unlimited}\:\mathrm{number}\:\mathrm{of}\:\mathrm{1kg},\:\mathrm{5kg} \\ $$$$\mathrm{10kg}\:\mathrm{and}\:\mathrm{25}\:\mathrm{kg}\:\mathrm{weights}.\:\mathrm{In}\:\mathrm{how}\:\mathrm{many}\:\mathrm{ways} \\ $$$$\mathrm{you}\:\mathrm{can}\:\mathrm{create}\:\mathrm{a}\:\mathrm{total}\:\mathrm{of}\:\mathrm{43kg}. \\ $$$$\mathrm{For}\:\mathrm{example} \\ $$$$\mathrm{43}×\mathrm{1} \\ $$$$\mathrm{5}×\mathrm{8}+\mathrm{3}×\mathrm{2} \\ $$$$\mathrm{etc}. \\ $$

Question Number 1468 Answers: 1 Comments: 0

$$ \\ $$

Question Number 1074 Answers: 0 Comments: 3

Prove by induction the following result where N is a positive even integer. S_1 ^2 +S_2 ^2 =2^N where S_1 =Σ_(r=1) ^((N/2)+1) (−1)^(r−1) ((N),((2(r−1))) ) and S_2 =Σ_(r=1) ^(N/2) (−1)^(r+1) ((N),((2r−1)) ) .

$${Prove}\:{by}\:{induction}\:{the}\:{following}\:{result}\:{where}\:{N}\:{is}\:{a}\:{positive}\:{even}\:{integer}.\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{S}_{\mathrm{1}} ^{\mathrm{2}} +{S}_{\mathrm{2}} ^{\mathrm{2}} =\mathrm{2}^{{N}} \\ $$$${where}\:\:\:\:{S}_{\mathrm{1}} =\underset{{r}=\mathrm{1}} {\overset{\frac{{N}}{\mathrm{2}}+\mathrm{1}} {\sum}}\left(−\mathrm{1}\right)^{{r}−\mathrm{1}} \begin{pmatrix}{{N}}\\{\mathrm{2}\left({r}−\mathrm{1}\right)}\end{pmatrix}\:\:\:\:{and}\:\:\:\:\:\:{S}_{\mathrm{2}} =\underset{{r}=\mathrm{1}} {\overset{{N}/\mathrm{2}} {\sum}}\left(−\mathrm{1}\right)^{{r}+\mathrm{1}} \begin{pmatrix}{{N}}\\{\mathrm{2}{r}−\mathrm{1}}\end{pmatrix}\:\:\:\:\:. \\ $$

Pg 20 Pg 21 Pg 22 Pg 23 Pg 24 Pg 25 Pg 26 Pg 27

Contact: info@tinkutara.com