Question and Answers Forum

All Questions Topic List

Permutation and CombinationQuestion and Answers: Page 20

Question Number 49101 Answers: 0 Comments: 0

Question Number 49100 Answers: 0 Comments: 0

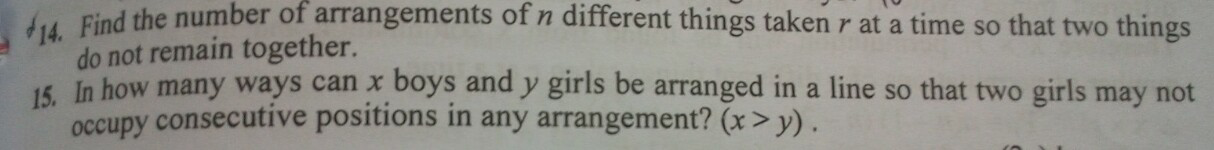
Question Number 49099 Answers: 0 Comments: 0

Question Number 49037 Answers: 0 Comments: 0

Question Number 49036 Answers: 1 Comments: 4

Question Number 49034 Answers: 1 Comments: 0

Question Number 48341 Answers: 0 Comments: 0

Question Number 47656 Answers: 1 Comments: 1

A square is divided into 9 identical smaller squares.Six identical balls are to be placed in these smaller squares such that each of the three rows gets at least one ball(one ball in one square only).In how many different ways can this be done? a)91 b)51 c)81 d)41

$${A}\:{square}\:{is}\:{divided}\:{into}\:\mathrm{9}\:{identical} \\ $$$${smaller}\:{squares}.{Six}\:{identical}\:{balls} \\ $$$${are}\:{to}\:{be}\:{placed}\:{in}\:{these}\:{smaller}\: \\ $$$${squares}\:{such}\:{that}\:{each}\:{of}\:{the}\:{three} \\ $$$${rows}\:{gets}\:{at}\:{least}\:{one}\:{ball}\left({one}\right. \\ $$$$\left.{ball}\:{in}\:{one}\:{square}\:{only}\right).{In}\:{how} \\ $$$${many}\:{different}\:{ways}\:{can}\:{this}\:{be} \\ $$$${done}? \\ $$$$\left.{a}\left.\right)\left.\mathrm{9}\left.\mathrm{1}\:{b}\right)\mathrm{51}\:{c}\right)\mathrm{81}\:{d}\right)\mathrm{41} \\ $$$$ \\ $$

Question Number 46143 Answers: 1 Comments: 0

Question Number 43824 Answers: 1 Comments: 0

Question Number 43659 Answers: 1 Comments: 2

An unfair coin with the probability of getting head in one toss = (1/5). If coin tosses n times, the probability of getting 2 heads is equal to the probability of getting 3 heads. Find n

$$\mathrm{An}\:\mathrm{unfair}\:\mathrm{coin}\:\mathrm{with}\:\mathrm{the}\:\mathrm{probability}\:\mathrm{of}\:\mathrm{getting} \\ $$$$\mathrm{head}\:\mathrm{in}\:\mathrm{one}\:\mathrm{toss}\:=\:\frac{\mathrm{1}}{\mathrm{5}}. \\ $$$$\mathrm{If}\:\mathrm{coin}\:\mathrm{tosses}\:{n}\:\mathrm{times},\:\mathrm{the}\:\mathrm{probability}\:\mathrm{of} \\ $$$$\mathrm{getting}\:\mathrm{2}\:\mathrm{heads}\:\mathrm{is}\:\mathrm{equal}\:\mathrm{to}\:\mathrm{the}\:\mathrm{probability}\:\mathrm{of}\: \\ $$$$\mathrm{getting}\:\mathrm{3}\:\mathrm{heads}.\:\mathrm{Find}\:{n} \\ $$

Question Number 43343 Answers: 1 Comments: 0

how many odd numbers greater than 60000 can be made from the digits 5,6,7,8,9,0 if no number contains any digit more than once?

$$\mathrm{how}\:\mathrm{many}\:\mathrm{odd}\:\mathrm{numbers}\:\mathrm{greater}\:\mathrm{than}\:\mathrm{60000}\:\mathrm{can}\:\mathrm{be}\:\mathrm{made} \\ $$$$\mathrm{from}\:\mathrm{the}\:\mathrm{digits}\:\mathrm{5},\mathrm{6},\mathrm{7},\mathrm{8},\mathrm{9},\mathrm{0}\:\mathrm{if}\:\mathrm{no}\:\mathrm{number}\:\mathrm{contains} \\ $$$$\mathrm{any}\:\mathrm{digit}\:\mathrm{more}\:\mathrm{than}\:\mathrm{once}? \\ $$

Question Number 43031 Answers: 2 Comments: 2

Question Number 42494 Answers: 1 Comments: 1

In the sequence of numbers 1, 2, 11, 22, 111, 222, ... the sum of the digits in 999th terms is ??

$$\mathrm{In}\:\mathrm{the}\:\mathrm{sequence}\:\mathrm{of}\:\mathrm{numbers}\:\:\mathrm{1},\:\mathrm{2},\:\mathrm{11},\:\mathrm{22},\:\mathrm{111},\:\mathrm{222},\:...\:\mathrm{the}\:\mathrm{sum}\:\mathrm{of}\:\mathrm{the}\:\mathrm{digits} \\ $$$$\mathrm{in}\:\mathrm{999th}\:\mathrm{terms}\:\mathrm{is}\:?? \\ $$

Question Number 42332 Answers: 0 Comments: 0

Question Number 42110 Answers: 1 Comments: 1

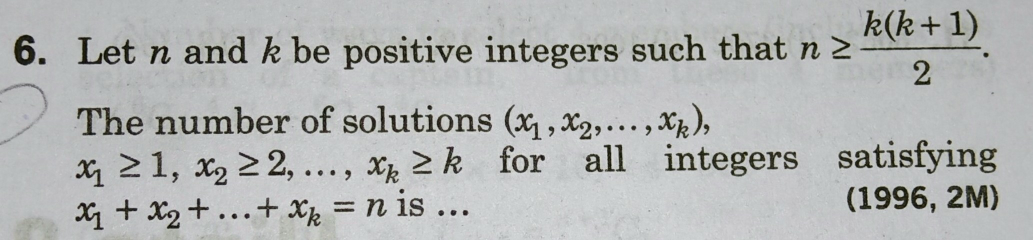
Question Number 42107 Answers: 0 Comments: 0

Question Number 42106 Answers: 1 Comments: 0

Question Number 41824 Answers: 3 Comments: 0

if ^n C_5 = ^n C_(11) find ^(18) C_n

$$\mathrm{if}\:\:\:\overset{\mathrm{n}} {\:}\mathrm{C}_{\mathrm{5}} \:=\:\overset{\mathrm{n}} {\:}\mathrm{C}_{\mathrm{11}} \:\:\:\mathrm{find}\:\:\:\:\:\:\overset{\mathrm{18}} {\:}\mathrm{C}_{\mathrm{n}} \\ $$

Question Number 40550 Answers: 1 Comments: 0

if three numbers are drawn at random successively without replacement from a set S={1,2,......10}then probability that the minimum of the choosen number is 3 or their maximum is 7 Answer=((11)/(40))

$$\mathrm{if}\:\mathrm{three}\:\mathrm{numbers}\:\mathrm{are}\:\mathrm{drawn}\:\mathrm{at}\:\mathrm{random} \\ $$$$\mathrm{successively}\:\mathrm{without}\:\mathrm{replacement}\:\mathrm{from} \\ $$$$\mathrm{a}\:\mathrm{set}\:\mathrm{S}=\left\{\mathrm{1},\mathrm{2},......\mathrm{10}\right\}\mathrm{then}\:\mathrm{probability}\:\mathrm{that} \\ $$$$\mathrm{the}\:\mathrm{minimum}\:\mathrm{of}\:\mathrm{the}\:\mathrm{choosen}\:\mathrm{number}\:\mathrm{is} \\ $$$$\mathrm{3}\:\mathrm{or}\:\mathrm{their}\:\mathrm{maximum}\:\mathrm{is}\:\mathrm{7}\:\:\:\:\:\:\:\: \\ $$$$\:\mathrm{Answer}=\frac{\mathrm{11}}{\mathrm{40}} \\ $$

Question Number 40216 Answers: 1 Comments: 0

Question Number 39846 Answers: 2 Comments: 2

the sum of the four digit even numbers that can be formed with digits 0 3 5 4 without repitation

$$\mathrm{the}\:\mathrm{sum}\:\mathrm{of}\:\mathrm{the}\:\mathrm{four}\:\:\mathrm{digit}\:\mathrm{even}\:\mathrm{numbers}\:\mathrm{that}\:\mathrm{can}\:\mathrm{be}\:\mathrm{formed}\:\mathrm{with}\:\mathrm{digits}\:\mathrm{0}\:\mathrm{3}\:\mathrm{5}\:\mathrm{4}\:\mathrm{without}\:\mathrm{repitation} \\ $$

Question Number 37648 Answers: 1 Comments: 0

A particle, of mass 5kg,moves in a straight line its displacement,x metres after t seconds is given by x = t^3 − 4t^2 +4t. Find the magnitude of the impulses exerted on the particle when t=2.

$$\mathrm{A}\:\mathrm{particle},\:\mathrm{of}\:\mathrm{mass}\:\mathrm{5kg},\mathrm{moves}\:\mathrm{in} \\ $$$$\mathrm{a}\:\mathrm{straight}\:\mathrm{line}\:\mathrm{its}\:\mathrm{displacement},\mathrm{x} \\ $$$$\mathrm{metres}\:\mathrm{after}\:\mathrm{t}\:\mathrm{seconds}\:\mathrm{is}\:\mathrm{given}\:\mathrm{by} \\ $$$${x}\:=\:{t}^{\mathrm{3}} −\:\mathrm{4}{t}^{\mathrm{2}} +\mathrm{4}{t}.\:{F}\mathrm{ind}\:\:\mathrm{the}\:\mathrm{magnitude} \\ $$$$\mathrm{of}\:\mathrm{the}\:\mathrm{impulses}\:\mathrm{exerted}\:\mathrm{on}\:\mathrm{the}\:\mathrm{particle} \\ $$$$\mathrm{when}\:\mathrm{t}=\mathrm{2}. \\ $$

Question Number 36784 Answers: 0 Comments: 0

Prove that Σ_(r=0) ^n r ((n),(r) )^2 = n (((2n − 1)),(( n − 1)) )

$$\mathrm{Prove}\:\mathrm{that} \\ $$$$\underset{{r}=\mathrm{0}} {\overset{{n}} {\sum}}\:{r}\:\begin{pmatrix}{{n}}\\{{r}}\end{pmatrix}^{\mathrm{2}} \:=\:{n}\:\begin{pmatrix}{\mathrm{2}{n}\:−\:\mathrm{1}}\\{\:\:{n}\:−\:\mathrm{1}}\end{pmatrix} \\ $$

Question Number 36398 Answers: 1 Comments: 1

Consider triangle ABC.If 206 lines are drawn from A to BC how many triangles are formed?

$${Consider}\:{triangle}\:{ABC}.{If}\:\mathrm{206} \\ $$$${lines}\:{are}\:{drawn}\:{from}\:{A}\:{to}\:{BC}\:{how} \\ $$$${many}\:{triangles}\:{are}\:{formed}? \\ $$

Question Number 35640 Answers: 1 Comments: 0

A panel of 3 women and 4 men is to be formed from 8 women and 7 men.Find the number of ways which the panel can be formed if it must contain at least 2 women.

$${A}\:{panel}\:{of}\:\mathrm{3}\:{women}\:{and}\:\mathrm{4}\:{men}\:{is} \\ $$$${to}\:{be}\:{formed}\:{from}\:\mathrm{8}\:{women}\:{and} \\ $$$$\mathrm{7}\:{men}.{Find}\:{the}\:{number}\:{of}\:{ways} \\ $$$${which}\:{the}\:{panel}\:{can}\:{be}\:{formed}\:{if} \\ $$$${it}\:{must}\:{contain}\:{at}\:{least}\:\mathrm{2}\:{women}. \\ $$

Pg 15 Pg 16 Pg 17 Pg 18 Pg 19 Pg 20 Pg 21 Pg 22 Pg 23 Pg 24

Contact: info@tinkutara.com