Question and Answers Forum

Permutation and CombinationQuestion and Answers: Page 19

Question Number 57909 Answers: 2 Comments: 0

n men and n women should be arranged alternately in a row, how many ways can this be done? if the same should be done on a table, how many ways then?

$${n}\:{men}\:{and}\:{n}\:{women}\:{should}\:{be}\:{arranged} \\ $$$${alternately}\:{in}\:{a}\:{row},\:{how}\:{many}\:{ways} \\ $$$${can}\:{this}\:{be}\:{done}?\:{if}\:{the}\:{same}\:{should} \\ $$$${be}\:{done}\:{on}\:{a}\:{table},\:{how}\:{many}\:{ways}\:{then}? \\ $$

Question Number 57688 Answers: 1 Comments: 12

Solve for n: Σ_i ^(n − 1) ^n C_i 2^i = 65, n ∈ Z^+ . where zero is included

$$\:\:\mathrm{Solve}\:\mathrm{for}\:\:\mathrm{n}:\:\:\:\:\:\:\:\:\underset{\mathrm{i}} {\overset{\mathrm{n}\:−\:\mathrm{1}} {\sum}}\:\:\:\overset{\mathrm{n}} {\:}\mathrm{C}_{\mathrm{i}} \:\mathrm{2}^{\mathrm{i}} \:\:=\:\:\mathrm{65},\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{n}\:\in\:\mathbb{Z}^{+} .\:\:\:\:\mathrm{where}\:\:\mathrm{zero}\:\mathrm{is}\: \\ $$$$\:\:\mathrm{included} \\ $$

Question Number 57363 Answers: 0 Comments: 3

Question Number 57336 Answers: 2 Comments: 0

If n be even, show that the expression ((n(n + 2)(n + 4) ... (2n − 2))/(1.3.5 ... (n − 1))) simplify to 2^(n − 1)

$$\mathrm{If}\:\:\mathrm{n}\:\mathrm{be}\:\mathrm{even},\:\mathrm{show}\:\mathrm{that}\:\mathrm{the}\:\mathrm{expression}\:\:\:\:\frac{\mathrm{n}\left(\mathrm{n}\:+\:\mathrm{2}\right)\left(\mathrm{n}\:+\:\mathrm{4}\right)\:...\:\left(\mathrm{2n}\:−\:\mathrm{2}\right)}{\mathrm{1}.\mathrm{3}.\mathrm{5}\:...\:\left(\mathrm{n}\:−\:\mathrm{1}\right)} \\ $$$$\mathrm{simplify}\:\mathrm{to}\:\:\mathrm{2}^{\mathrm{n}\:−\:\mathrm{1}} \\ $$

Question Number 57048 Answers: 2 Comments: 1

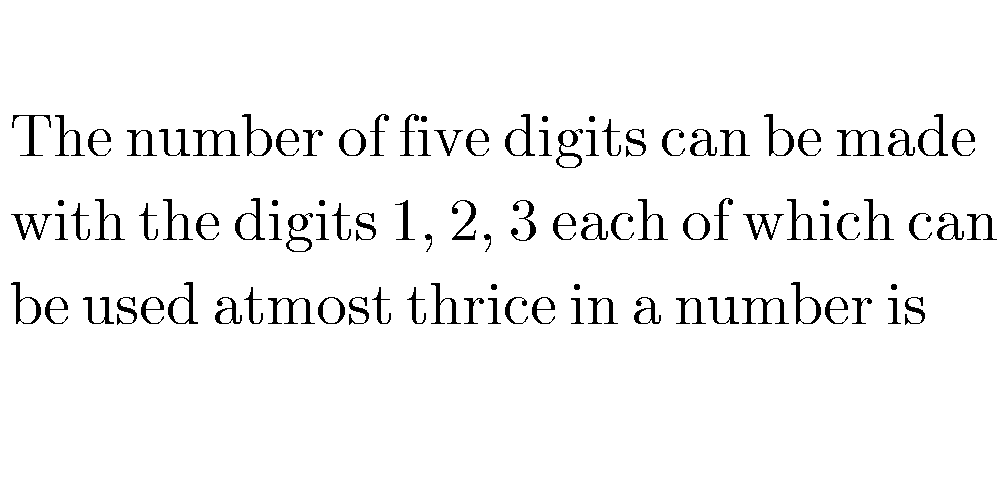
Question Number 57046 Answers: 0 Comments: 1

Question Number 57042 Answers: 1 Comments: 1

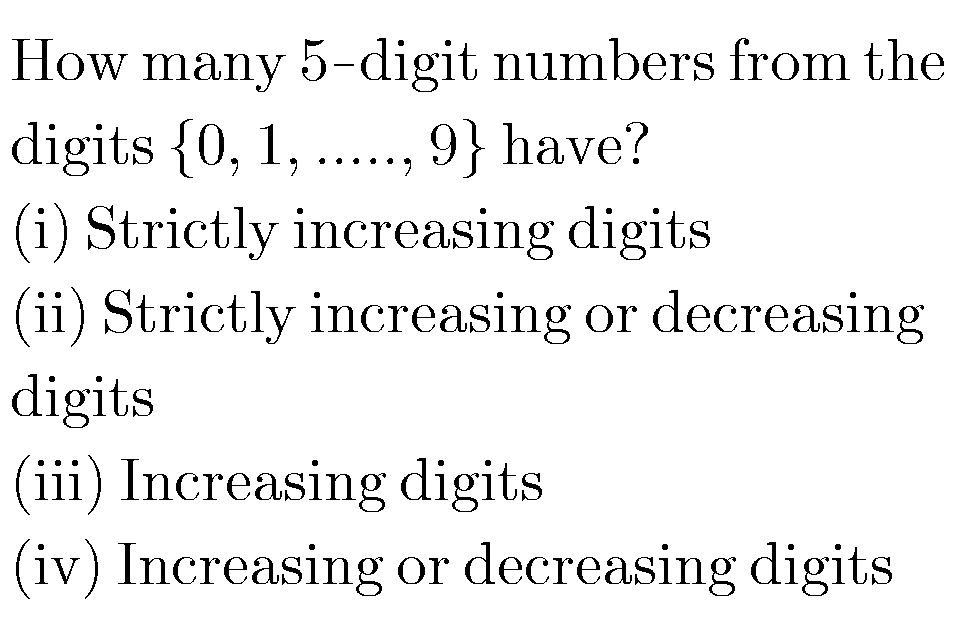
Question Number 56961 Answers: 1 Comments: 0

Out of 6 mathematicians and 7 physicists a committee consisting of 3 mathematicians and 3 physicists is to be formed. In how many ways can this be done if two particular mathematicians cannot be on the commitee?

$$\mathrm{Out}\:\mathrm{of}\:\mathrm{6}\:\mathrm{mathematicians}\:\mathrm{and}\:\mathrm{7}\:\mathrm{physicists} \\ $$$$\mathrm{a}\:\mathrm{committee}\:\mathrm{consisting}\:\mathrm{of}\:\mathrm{3}\:\mathrm{mathematicians} \\ $$$$\mathrm{and}\:\mathrm{3}\:\mathrm{physicists}\:\mathrm{is}\:\mathrm{to}\:\mathrm{be}\:\mathrm{formed}.\:\mathrm{In}\:\mathrm{how} \\ $$$$\mathrm{many}\:\mathrm{ways}\:\mathrm{can}\:\mathrm{this}\:\mathrm{be}\:\mathrm{done}\:\mathrm{if}\:\mathrm{two}\: \\ $$$$\mathrm{particular}\:\mathrm{mathematicians}\:\mathrm{cannot}\:\mathrm{be} \\ $$$$\mathrm{on}\:\mathrm{the}\:\mathrm{commitee}? \\ $$

Question Number 56913 Answers: 1 Comments: 2

How many possible solution sets that satisfy x_1 + x_2 + x_3 + x_4 = 5 with 0 ≤ x_1 ≤ 3 0 ≤ x_2 ≤ 3 0 ≤ x_3 ≤ 2 0 ≤ x_4 ≤ 2

$$\mathrm{How}\:\mathrm{many}\:\mathrm{possible}\:\mathrm{solution}\:\mathrm{sets}\:\mathrm{that}\:\mathrm{satisfy}\: \\ $$$${x}_{\mathrm{1}} \:+\:{x}_{\mathrm{2}} \:+\:{x}_{\mathrm{3}} \:+\:{x}_{\mathrm{4}} \:=\:\mathrm{5} \\ $$$$\mathrm{with} \\ $$$$\mathrm{0}\:\leqslant\:{x}_{\mathrm{1}} \:\leqslant\:\mathrm{3}\:\: \\ $$$$\mathrm{0}\:\leqslant\:{x}_{\mathrm{2}} \:\leqslant\:\mathrm{3} \\ $$$$\mathrm{0}\:\leqslant\:{x}_{\mathrm{3}} \:\leqslant\:\mathrm{2} \\ $$$$\mathrm{0}\:\leqslant\:{x}_{\mathrm{4}} \:\leqslant\:\mathrm{2} \\ $$

Question Number 56820 Answers: 0 Comments: 0

the no of traingle formed by the vertices of a decagon such that atleast one side is in common

$$\mathrm{the}\:\mathrm{no}\:\mathrm{of}\:\mathrm{traingle}\:\mathrm{formed}\:\mathrm{by}\:\mathrm{the}\:\mathrm{vertices} \\ $$$$\mathrm{of}\:\mathrm{a}\:\mathrm{decagon}\:\mathrm{such}\:\mathrm{that}\:\mathrm{atleast}\:\mathrm{one}\:\mathrm{side} \\ $$$$\mathrm{is}\:\mathrm{in}\:\mathrm{common} \\ $$

Question Number 56784 Answers: 0 Comments: 0

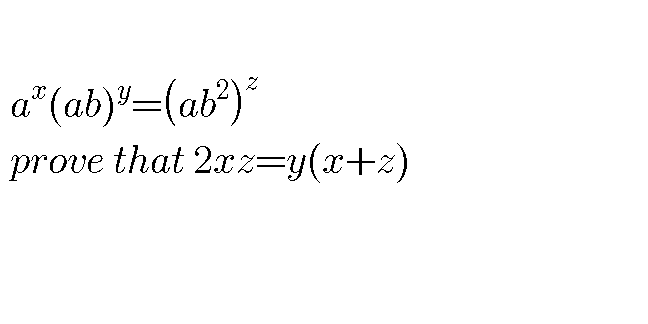
Question Number 56743 Answers: 1 Comments: 0

Question Number 56688 Answers: 1 Comments: 0

How many odd numbers, greater than 60000, can be made from the digits 5,6,7,8,9,0, if no number contains any digit more than ones?

$$\mathrm{How}\:\mathrm{many}\:\mathrm{odd}\:\mathrm{numbers},\:\mathrm{greater}\:\mathrm{than} \\ $$$$\mathrm{60000},\:\mathrm{can}\:\mathrm{be}\:\mathrm{made}\:\mathrm{from}\:\mathrm{the}\:\mathrm{digits} \\ $$$$\mathrm{5},\mathrm{6},\mathrm{7},\mathrm{8},\mathrm{9},\mathrm{0},\:\mathrm{if}\:\mathrm{no}\:\mathrm{number}\:\mathrm{contains}\:\mathrm{any} \\ $$$$\mathrm{digit}\:\mathrm{more}\:\mathrm{than}\:\mathrm{ones}? \\ $$

Question Number 56678 Answers: 1 Comments: 0

A box contains 9 whites, 7 red and 4 blue balls. Three balls are picked at random, one after the other without replacement. a) find the probability that: i. they are all of the same color ii. there is one of each colour iii. two of them are red b) if it is known that the first one picked is blue, find the probability that the rest are white.

$$\mathrm{A}\:\mathrm{box}\:\mathrm{contains}\:\mathrm{9}\:\mathrm{whites},\:\mathrm{7}\:\mathrm{red}\:\mathrm{and}\:\mathrm{4}\:\mathrm{blue} \\ $$$$\mathrm{balls}.\:\mathrm{Three}\:\mathrm{balls}\:\mathrm{are}\:\mathrm{picked}\:\mathrm{at}\:\mathrm{random}, \\ $$$$\mathrm{one}\:\mathrm{after}\:\mathrm{the}\:\mathrm{other}\:\mathrm{without}\:\mathrm{replacement}. \\ $$$$\left.\mathrm{a}\right)\:\mathrm{find}\:\mathrm{the}\:\mathrm{probability}\:\mathrm{that}: \\ $$$$\mathrm{i}.\:\mathrm{they}\:\mathrm{are}\:\mathrm{all}\:\mathrm{of}\:\mathrm{the}\:\mathrm{same}\:\mathrm{color} \\ $$$$\mathrm{ii}.\:\mathrm{there}\:\mathrm{is}\:\mathrm{one}\:\mathrm{of}\:\mathrm{each}\:\mathrm{colour} \\ $$$$\mathrm{iii}.\:\mathrm{two}\:\mathrm{of}\:\mathrm{them}\:\mathrm{are}\:\mathrm{red} \\ $$$$\left.\mathrm{b}\right)\:\mathrm{if}\:\mathrm{it}\:\mathrm{is}\:\mathrm{known}\:\mathrm{that}\:\mathrm{the}\:\mathrm{first}\:\mathrm{one}\:\mathrm{picked} \\ $$$$\mathrm{is}\:\mathrm{blue},\:\mathrm{find}\:\mathrm{the}\:\mathrm{probability}\:\mathrm{that}\:\mathrm{the}\:\mathrm{rest} \\ $$$$\mathrm{are}\:\mathrm{white}. \\ $$

Question Number 56624 Answers: 0 Comments: 2

How many numbers greater than 2000 can be formed using the digits 1,3,4,5,6? how many of these will be even? repetition not allowed.

$$\mathrm{How}\:\mathrm{many}\:\mathrm{numbers}\:\mathrm{greater}\:\mathrm{than}\:\mathrm{2000} \\ $$$$\mathrm{can}\:\mathrm{be}\:\mathrm{formed}\:\mathrm{using}\:\mathrm{the}\:\mathrm{digits}\:\mathrm{1},\mathrm{3},\mathrm{4},\mathrm{5},\mathrm{6}? \\ $$$$\mathrm{how}\:\mathrm{many}\:\mathrm{of}\:\mathrm{these}\:\mathrm{will}\:\mathrm{be}\:\mathrm{even}? \\ $$$$\mathrm{repetition}\:\mathrm{not}\:\mathrm{allowed}. \\ $$

Question Number 56615 Answers: 0 Comments: 4

In how many different ways can the letters of the word OKINKWO be arranged? In how many of these arrangements does an O occupy both end points of the word?

$$\mathrm{In}\:\mathrm{how}\:\mathrm{many}\:\mathrm{different}\:\mathrm{ways}\:\mathrm{can}\:\mathrm{the} \\ $$$$\mathrm{letters}\:\mathrm{of}\:\mathrm{the}\:\mathrm{word}\:\mathrm{OKINKWO}\:\mathrm{be}\:\mathrm{arranged}?\: \\ $$$$\mathrm{In}\:\mathrm{how}\:\mathrm{many}\:\mathrm{of}\:\mathrm{these}\:\mathrm{arrangements} \\ $$$$\mathrm{does}\:\mathrm{an}\:\mathrm{O}\:\mathrm{occupy}\:\mathrm{both}\:\mathrm{end}\:\mathrm{points}\:\mathrm{of} \\ $$$$\mathrm{the}\:\mathrm{word}? \\ $$

Question Number 56212 Answers: 1 Comments: 0

In how many ways can 4 boys and 3 girls stand in a straight line a. if there are no restrictions b. if the boys stand next to each other

$$\mathrm{In}\:\mathrm{how}\:\mathrm{many}\:\mathrm{ways}\:\mathrm{can}\:\mathrm{4}\:\mathrm{boys}\:\mathrm{and}\:\mathrm{3}\:\mathrm{girls} \\ $$$$\mathrm{stand}\:\mathrm{in}\:\mathrm{a}\:\mathrm{straight}\:\mathrm{line} \\ $$$$\mathrm{a}.\:\mathrm{if}\:\mathrm{there}\:\mathrm{are}\:\mathrm{no}\:\mathrm{restrictions} \\ $$$$\mathrm{b}.\:\mathrm{if}\:\mathrm{the}\:\mathrm{boys}\:\mathrm{stand}\:\mathrm{next}\:\mathrm{to}\:\mathrm{each}\:\mathrm{other} \\ $$

Question Number 56025 Answers: 2 Comments: 0

Find the probability that a student arranging the letters of the word MATHEMATICS will make all the vowels be together in any arrangement he or she does.

$$\mathrm{Find}\:\mathrm{the}\:\mathrm{probability}\:\mathrm{that}\:\mathrm{a}\:\mathrm{student} \\ $$$$\mathrm{arranging}\:\mathrm{the}\:\mathrm{letters}\:\mathrm{of}\:\mathrm{the}\:\mathrm{word} \\ $$$$\mathrm{MATHEMATICS}\:\mathrm{will}\:\mathrm{make}\:\mathrm{all}\:\mathrm{the} \\ $$$$\mathrm{vowels}\:\mathrm{be}\:\mathrm{together}\:\mathrm{in}\:\mathrm{any}\:\mathrm{arrangement} \\ $$$$\mathrm{he}\:\mathrm{or}\:\mathrm{she}\:\mathrm{does}. \\ $$

Question Number 55502 Answers: 2 Comments: 1