Question and Answers Forum

Permutation and CombinationQuestion and Answers: Page 10

Question Number 137745 Answers: 1 Comments: 0

Each of the digits 2, 4, 6, and 8 can be used once and once only in writing a four-digit number. What is the sum of all such numbers that are divisible by 11?

$$ \\ $$Each of the digits 2, 4, 6, and 8 can be used once and once only in writing a four-digit number. What is the sum of all such numbers that are divisible by 11?

Question Number 137035 Answers: 1 Comments: 1

Given a 10−digit number X = 1345789026 How many 10−digit number that can be made using every digit from X, with condition: If a number n is located in k^(th) position of X, then the new created number must not contain number n in k^(th) position Example: • Number 1 is located in 1^(st) position of X, hence 1234567890 is not valid, but 2134567890 is valid • Number 5 and 0 are located in 4^(th) and 8^(th) position of X, hence 9435162087 is not valid, but 9431506287 is valid. • 1345026789 is not valid • and so on...

$$\mathrm{Given}\:\mathrm{a}\:\mathrm{10}−\mathrm{digit}\:\mathrm{number}\:{X}\:=\:\mathrm{1345789026} \\ $$$$\mathrm{How}\:\mathrm{many}\:\mathrm{10}−\mathrm{digit}\:\mathrm{number}\:\mathrm{that}\:\mathrm{can}\:\mathrm{be}\:\mathrm{made} \\ $$$$\mathrm{using}\:\mathrm{every}\:\mathrm{digit}\:\mathrm{from}\:{X},\:\mathrm{with}\:\mathrm{condition}: \\ $$$$\mathrm{If}\:\mathrm{a}\:\mathrm{number}\:{n}\:\:\mathrm{is}\:\mathrm{located}\:\mathrm{in}\:{k}^{{th}} \:\mathrm{position}\:\mathrm{of}\:{X},\:\mathrm{then} \\ $$$$\mathrm{the}\:\mathrm{new}\:\mathrm{created}\:\mathrm{number}\:\mathrm{must}\:\mathrm{not}\:\mathrm{contain} \\ $$$$\mathrm{number}\:{n}\:\mathrm{in}\:{k}^{{th}} \:\mathrm{position} \\ $$$$ \\ $$$$\mathrm{Example}: \\ $$$$\bullet\:\mathrm{Number}\:\mathrm{1}\:\mathrm{is}\:\mathrm{located}\:\mathrm{in}\:\mathrm{1}^{{st}} \:\mathrm{position}\:\mathrm{of}\:{X},\:\mathrm{hence} \\ $$$$\mathrm{1234567890}\:\mathrm{is}\:\mathrm{not}\:\mathrm{valid},\:\mathrm{but}\:\mathrm{2134567890} \\ $$$$\mathrm{is}\:\mathrm{valid} \\ $$$$\bullet\:\mathrm{Number}\:\mathrm{5}\:\mathrm{and}\:\mathrm{0}\:\mathrm{are}\:\mathrm{located}\:\mathrm{in}\:\mathrm{4}^{{th}} \:\mathrm{and}\:\mathrm{8}^{{th}} \:\mathrm{position} \\ $$$$\mathrm{of}\:{X},\:\mathrm{hence}\:\mathrm{9435162087}\:\mathrm{is}\:\mathrm{not}\:\mathrm{valid},\:\mathrm{but} \\ $$$$\mathrm{9431506287}\:\mathrm{is}\:\mathrm{valid}. \\ $$$$\bullet\:\mathrm{1345026789}\:\mathrm{is}\:\mathrm{not}\:\mathrm{valid} \\ $$$$\bullet\:\mathrm{and}\:\mathrm{so}\:\mathrm{on}... \\ $$

Question Number 136872 Answers: 0 Comments: 4

Question Number 136448 Answers: 1 Comments: 0

Mr.A wants to deliver 7 letters to his 7 friends so that each gets 1 letter. All of the letters are written of the addresses of his 7 friends. Find the probbility that, 3 of his friends receive the correct letters and the remaining 4 receive the wrong ones.

$$\mathrm{Mr}.\mathrm{A}\:\mathrm{wants}\:\mathrm{to}\:\mathrm{deliver}\:\mathrm{7}\:\mathrm{letters}\:\mathrm{to}\:\mathrm{his}\:\mathrm{7}\:\mathrm{friends}\:\mathrm{so}\:\mathrm{that}\:\mathrm{each}\:\mathrm{gets}\:\mathrm{1}\:\mathrm{letter}. \\ $$$$\mathrm{All}\:\mathrm{of}\:\mathrm{the}\:\mathrm{letters}\:\mathrm{are}\:\mathrm{written}\:\mathrm{of}\:\mathrm{the}\:\mathrm{addresses}\:\mathrm{of}\:\mathrm{his}\:\mathrm{7}\:\mathrm{friends}.\:\mathrm{Find}\:\mathrm{the}\:\mathrm{probbility}\:\mathrm{that}, \\ $$$$\mathrm{3}\:\mathrm{of}\:\mathrm{his}\:\mathrm{friends}\:\mathrm{receive}\:\mathrm{the}\:\mathrm{correct}\:\mathrm{letters}\:\mathrm{and}\:\mathrm{the}\:\mathrm{remaining}\:\mathrm{4}\:\mathrm{receive}\:\mathrm{the}\:\mathrm{wrong}\:\mathrm{ones}. \\ $$

Question Number 136417 Answers: 2 Comments: 0

Question Number 135797 Answers: 1 Comments: 0

How do you solve f(3) when f(-1) = -1 and f(0) =1 and f(x) =f(x-1)-2f(x-2)?

$$ \\ $$How do you solve f(3) when f(-1) = -1 and f(0) =1 and f(x) =f(x-1)-2f(x-2)?

Question Number 135599 Answers: 1 Comments: 0

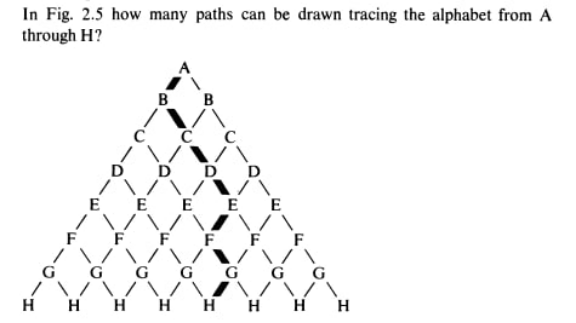
Question Number 135490 Answers: 3 Comments: 0

Combination A committee of 8 people is to be formed from 7 women and 5 men. In how many ways can the members be chosen so as to include at least 3 men?

$${Combination} \\ $$A committee of 8 people is to be formed from 7 women and 5 men. In how many ways can the members be chosen so as to include at least 3 men?

Question Number 135303 Answers: 2 Comments: 0

in how many ways can 10 people be seated in a round table if 3 persons want to seat consecutively?

$$ \\ $$in how many ways can 10 people be seated in a round table if 3 persons want to seat consecutively?

Question Number 135239 Answers: 0 Comments: 0

Question Number 135218 Answers: 2 Comments: 0

Permutation How many ways can 10 men and 7 women sit at a round table so that no 2 women are next to each other? 😎😎😎😎

$$\mathrm{Permutation} \\ $$How many ways can 10 men and 7 women sit at a round table so that no 2 women are next to each other? 😎😎😎😎

Question Number 135024 Answers: 0 Comments: 7

Question Number 134905 Answers: 2 Comments: 1

Combinatorics What is the number of ways of distributing 9 different objects among 5 persons such that each gets at least 1?

$$\mathrm{Combinatorics} \\ $$What is the number of ways of distributing 9 different objects among 5 persons such that each gets at least 1?

Question Number 134798 Answers: 3 Comments: 0

Binomial theorem Given that the coefficient of x^2 in the expansion of (1+ax) (3-2 x) ^5 is 1440, what is the value of the constant a?

$$\mathrm{Binomial}\:\mathrm{theorem} \\ $$Given that the coefficient of x^2 in the expansion of (1+ax) (3-2 x) ^5 is 1440, what is the value of the constant a?

Question Number 134644 Answers: 1 Comments: 1

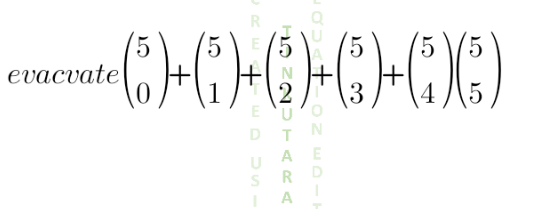
Question Number 134482 Answers: 0 Comments: 5

How many ways can this be done if you distribute 25 identical pieces of candy among five children?

$$ \\ $$How many ways can this be done if you distribute 25 identical pieces of candy among five children?

Question Number 134389 Answers: 1 Comments: 0

Eight dice are tossed. If the dice are identical in appearance , how many different−looking (distinguishable) occurrences are there?

$$\mathrm{Eight}\:\mathrm{dice}\:\mathrm{are}\:\mathrm{tossed}.\:\mathrm{If}\:\mathrm{the}\:\mathrm{dice}\:\mathrm{are}\:\mathrm{identical}\:\mathrm{in} \\ $$$$\mathrm{appearance}\:,\:\mathrm{how}\:\mathrm{many}\:\mathrm{different}−\mathrm{looking}\: \\ $$$$\left(\mathrm{distinguishable}\right)\:\mathrm{occurrences}\:\mathrm{are}\:\mathrm{there}? \\ $$

Question Number 134329 Answers: 2 Comments: 0

How many ways can 15 basketball players be assigned to Team A, Team B, and Team C with 5 players on each team?

$$ \\ $$How many ways can 15 basketball players be assigned to Team A, Team B, and Team C with 5 players on each team?

Question Number 134292 Answers: 1 Comments: 0

The digits 1, 2, 3, 4, 5, 6, and 7 are written on separate cards. Three are drawn and placed in order of drawing. In how many ways can numbers greater than 500 be formed?

$$ \\ $$The digits 1, 2, 3, 4, 5, 6, and 7 are written on separate cards. Three are drawn and placed in order of drawing. In how many ways can numbers greater than 500 be formed?

Question Number 134232 Answers: 2 Comments: 0

In how many ways can 5 men, 4 women, and 3 children be arranged in a row of 12 seats if the children sit together?

$$ \\ $$In how many ways can 5 men, 4 women, and 3 children be arranged in a row of 12 seats if the children sit together?

Question Number 134205 Answers: 0 Comments: 1

The numbers 1,2,3,4,5,6,7,8,9 and 10 are written around a circle in arbitrary order. We add all the numbers with their neighbours, we get 10 sums that way. What is the maximum possible value of the smallest of these sums?

$$ \\ $$The numbers 1,2,3,4,5,6,7,8,9 and 10 are written around a circle in arbitrary order. We add all the numbers with their neighbours, we get 10 sums that way. What is the maximum possible value of the smallest of these sums?

Question Number 133995 Answers: 0 Comments: 2

in how many ways can n men and n women be arranged in a row such that men and women alternate?

$${in}\:{how}\:{many}\:{ways}\:{can}\:{n}\:{men}\:{and} \\ $$$${n}\:{women}\:{be}\:{arranged}\:{in}\:{a}\:{row}\:{such} \\ $$$${that}\:{men}\:{and}\:{women}\:{alternate}? \\ $$

Question Number 133682 Answers: 0 Comments: 2

Question Number 133658 Answers: 0 Comments: 3

Question Number 133642 Answers: 4 Comments: 1

Question Number 133316 Answers: 2 Comments: 1

How many 6−letter words in which at least one letter appears more than once ,can be made from the letters in the word FLIGHT

$$\mathrm{How}\:\mathrm{many}\:\mathrm{6}−\mathrm{letter}\:\mathrm{words}\:\mathrm{in}\: \\ $$$$\mathrm{which}\:\mathrm{at}\:\mathrm{least}\:\mathrm{one}\:\mathrm{letter}\:\mathrm{appears} \\ $$$$\mathrm{more}\:\mathrm{than}\:\mathrm{once}\:,\mathrm{can}\:\mathrm{be}\:\mathrm{made}\:\mathrm{from} \\ $$$$\mathrm{the}\:\mathrm{letters}\:\mathrm{in}\:\mathrm{the}\:\mathrm{word}\:\mathrm{FLIGHT} \\ $$$$ \\ $$

Pg 5 Pg 6 Pg 7 Pg 8 Pg 9 Pg 10 Pg 11 Pg 12 Pg 13 Pg 14

Contact: info@tinkutara.com