
Question Number 33834 by uddipan last updated on 25/Apr/18
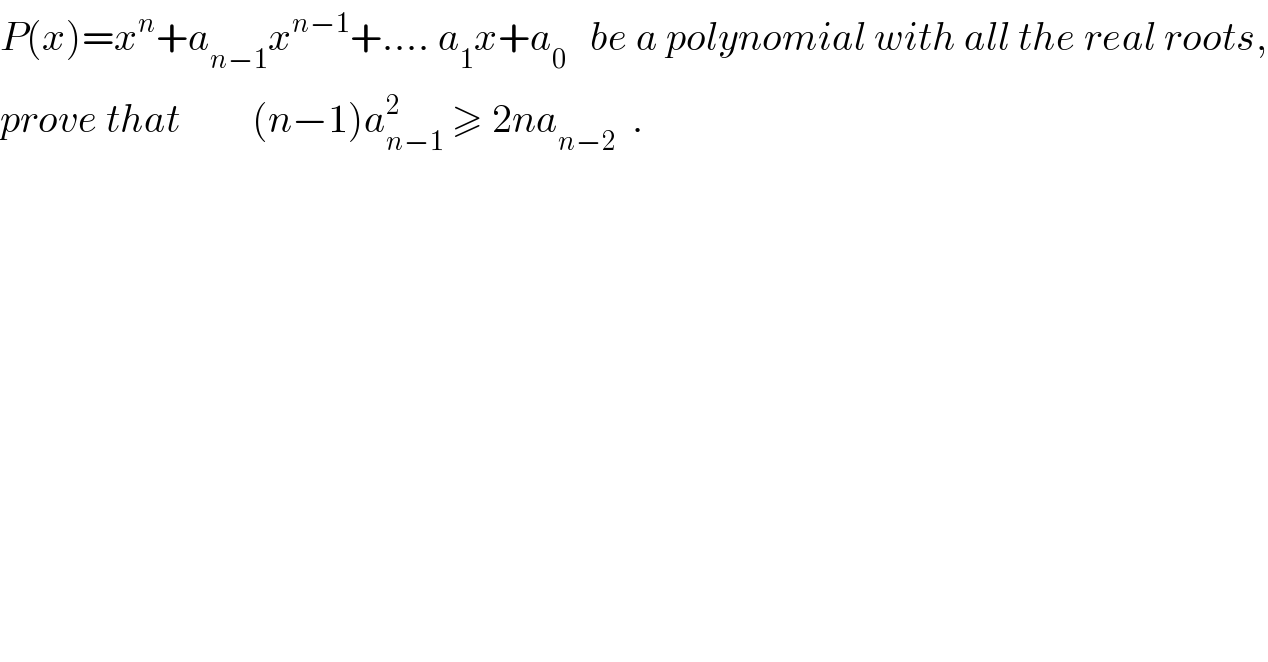
$${P}\left({x}\right)={x}^{{n}} +{a}_{{n}−\mathrm{1}} {x}^{{n}−\mathrm{1}} +....\:{a}_{\mathrm{1}} {x}+{a}_{\mathrm{0}} \:\:\:{be}\:{a}\:{polynomial}\:{with}\:{all}\:{the}\:{real}\:{roots}, \\ $$$${prove}\:{that}\:\:\:\:\:\:\:\:\:\left({n}−\mathrm{1}\right){a}_{{n}−\mathrm{1}} ^{\mathrm{2}} \:\geqslant\:\mathrm{2}{na}_{{n}−\mathrm{2}} \:\:. \\ $$
