
Question Number 188082 by Shrinava last updated on 25/Feb/23
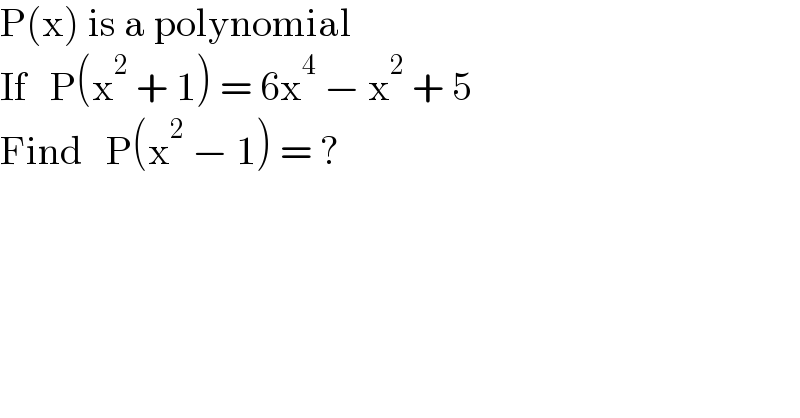
$$\mathrm{P}\left(\mathrm{x}\right)\:\mathrm{is}\:\mathrm{a}\:\mathrm{polynomial} \\ $$$$\mathrm{If}\:\:\:\mathrm{P}\left(\mathrm{x}^{\mathrm{2}} \:+\:\mathrm{1}\right)\:=\:\mathrm{6x}^{\mathrm{4}} \:−\:\mathrm{x}^{\mathrm{2}} \:+\:\mathrm{5} \\ $$$$\mathrm{Find}\:\:\:\mathrm{P}\left(\mathrm{x}^{\mathrm{2}} \:−\:\mathrm{1}\right)\:=\:? \\ $$
Answered by cortano12 last updated on 25/Feb/23
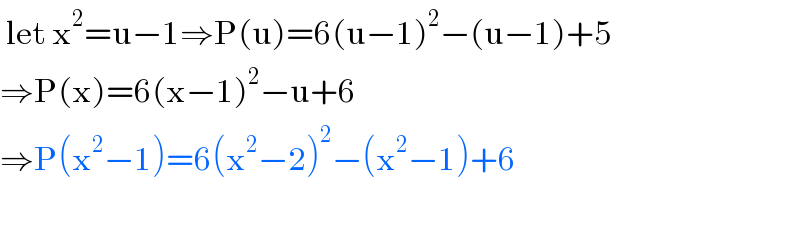
$$\:\mathrm{let}\:\mathrm{x}^{\mathrm{2}} =\mathrm{u}−\mathrm{1}\Rightarrow\mathrm{P}\left(\mathrm{u}\right)=\mathrm{6}\left(\mathrm{u}−\mathrm{1}\right)^{\mathrm{2}} −\left(\mathrm{u}−\mathrm{1}\right)+\mathrm{5} \\ $$$$\Rightarrow\mathrm{P}\left(\mathrm{x}\right)=\mathrm{6}\left(\mathrm{x}−\mathrm{1}\right)^{\mathrm{2}} −\mathrm{u}+\mathrm{6} \\ $$$$\Rightarrow\mathrm{P}\left(\mathrm{x}^{\mathrm{2}} −\mathrm{1}\right)=\mathrm{6}\left(\mathrm{x}^{\mathrm{2}} −\mathrm{2}\right)^{\mathrm{2}} −\left(\mathrm{x}^{\mathrm{2}} −\mathrm{1}\right)+\mathrm{6} \\ $$$$ \\ $$
