
Question Number 127684 by liberty last updated on 01/Jan/21
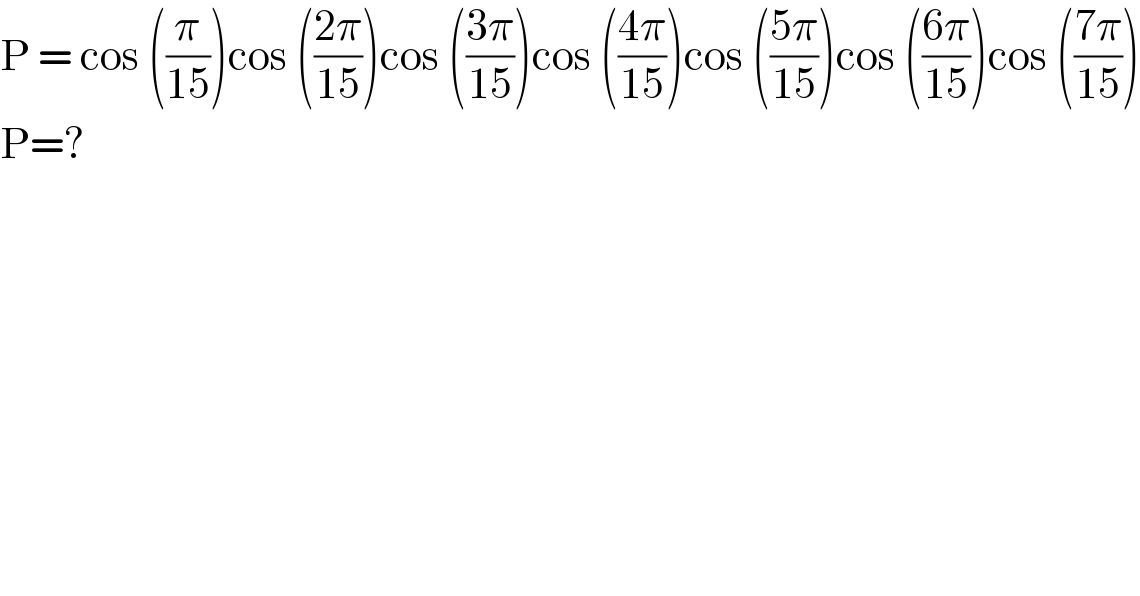
$$\mathrm{P}\:=\:\mathrm{cos}\:\left(\frac{\pi}{\mathrm{15}}\right)\mathrm{cos}\:\left(\frac{\mathrm{2}\pi}{\mathrm{15}}\right)\mathrm{cos}\:\left(\frac{\mathrm{3}\pi}{\mathrm{15}}\right)\mathrm{cos}\:\left(\frac{\mathrm{4}\pi}{\mathrm{15}}\right)\mathrm{cos}\:\left(\frac{\mathrm{5}\pi}{\mathrm{15}}\right)\mathrm{cos}\:\left(\frac{\mathrm{6}\pi}{\mathrm{15}}\right)\mathrm{cos}\:\left(\frac{\mathrm{7}\pi}{\mathrm{15}}\right) \\ $$$$\mathrm{P}=?\: \\ $$
Answered by bramlexs22 last updated on 01/Jan/21

Commented by bobhans last updated on 01/Jan/21
$${nice}\:...{happy}\:{new}\:{year}... \\ $$
Commented by bramlexs22 last updated on 01/Jan/21
happy new year too
Commented by Apurv last updated on 01/Jan/21

$$ \\ $$$$\mathrm{P}\:=\:\mathrm{cos}\:\left(\frac{\pi}{\mathrm{15}}\right)\mathrm{cos}\:\left(\frac{\mathrm{2}\pi}{\mathrm{15}}\right)\mathrm{cos}\:\left(\frac{\mathrm{3}\pi}{\mathrm{15}}\right)\mathrm{cos}\:\left(\frac{\mathrm{4}\pi}{\mathrm{15}}\right)\mathrm{cos}\:\left(\frac{\mathrm{5}\pi}{\mathrm{15}}\right)\mathrm{cos}\:\left(\frac{\mathrm{6}\pi}{\mathrm{15}}\right)\mathrm{cos}\:\left(\frac{\mathrm{7}\pi}{\mathrm{15}}\right) \\ $$$$\mathrm{P}= \\ $$
Answered by mindispower last updated on 01/Jan/21
![cos(x)=((e^(ix) +e^(−ix) )/2)=(e^x /2)(1+e^(2ix) ) let p(x)=X^(15) −1=0 p(x)=0⇒X=e^(2((ikπ)/(15))) ,k∈{0,.....,14} P(x)=Π_(k=0) ^(14) (X−e^(2((ikπ)/(15))) ),P(−1)=−Π_(k=0) ^(14) ^ (1+e^(i2((kπ)/(15 ))) )=−2 =Π_(k=0) ^(14) e^((ikπ)/(15)) (e^((iπk)/(15)) +e^(−((ikπ)/(15))) )=−2^(15) e^(((iπ)/(15))(15.7)) .Π_(k=0) ^(14) cos(((kπ)/(15))) ⇒(1/2^(14) )=.−1Π_(k=1) ^7 cos(((kπ)/(15))).Π_(k=8) ^(14) cos(((kπ)/(15))) k→15−k,in 2nd ⇒(1/2^(14) )=−Π_(k=1) ^7 cos(((kπ)/(15))).Π_(k=1) ^7 cos(π−((kπ)/(15))) (1/2^(14) )=(Π_1 ^7 cos(((kπ)/(15))))^2 ⇒Π_(k.1) ^7 cos(((kπ)/(15)))=+_− (1/2^7 ),∀k∈[1,7]∩N 0≤((kπ)/(15))≤(π/2) cos(((kπ)/(15)))≥0⇒P=(1/(128))](Q127705.png)
$${cos}\left({x}\right)=\frac{{e}^{{ix}} +{e}^{−{ix}} }{\mathrm{2}}=\frac{{e}^{{x}} }{\mathrm{2}}\left(\mathrm{1}+{e}^{\mathrm{2}{ix}} \right) \\ $$$${let}\:{p}\left({x}\right)={X}^{\mathrm{15}} −\mathrm{1}=\mathrm{0} \\ $$$${p}\left({x}\right)=\mathrm{0}\Rightarrow{X}={e}^{\mathrm{2}\frac{{ik}\pi}{\mathrm{15}}} \:,{k}\in\left\{\mathrm{0},.....,\mathrm{14}\right\} \\ $$$${P}\left({x}\right)=\underset{{k}=\mathrm{0}} {\overset{\mathrm{14}} {\prod}}\:\left({X}−{e}^{\mathrm{2}\frac{{ik}\pi}{\mathrm{15}}} \:\right),{P}\left(−\mathrm{1}\right)=−\underset{{k}=\mathrm{0}} {\overset{\mathrm{14}} {\prod}}\overset{} {\:}\left(\mathrm{1}+{e}^{{i}\mathrm{2}\frac{{k}\pi}{\mathrm{15}\:\:}} \right)=−\mathrm{2} \\ $$$$=\underset{{k}=\mathrm{0}} {\overset{\mathrm{14}} {\prod}}{e}^{\frac{{ik}\pi}{\mathrm{15}}} \left({e}^{\frac{{i}\pi{k}}{\mathrm{15}}} +{e}^{−\frac{{ik}\pi}{\mathrm{15}}} \right)=−\mathrm{2}^{\mathrm{15}} {e}^{\frac{{i}\pi}{\mathrm{15}}\left(\mathrm{15}.\mathrm{7}\right)} .\underset{{k}=\mathrm{0}} {\overset{\mathrm{14}} {\prod}}{cos}\left(\frac{{k}\pi}{\mathrm{15}}\right) \\ $$$$\Rightarrow\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{14}} }=.−\mathrm{1}\underset{{k}=\mathrm{1}} {\overset{\mathrm{7}} {\prod}}{cos}\left(\frac{{k}\pi}{\mathrm{15}}\right).\underset{{k}=\mathrm{8}} {\overset{\mathrm{14}} {\prod}}{cos}\left(\frac{{k}\pi}{\mathrm{15}}\right) \\ $$$${k}\rightarrow\mathrm{15}−{k},{in}\:\mathrm{2}{nd}\: \\ $$$$\Rightarrow\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{14}} }=−\underset{{k}=\mathrm{1}} {\overset{\mathrm{7}} {\prod}}{cos}\left(\frac{{k}\pi}{\mathrm{15}}\right).\underset{{k}=\mathrm{1}} {\overset{\mathrm{7}} {\prod}}{cos}\left(\pi−\frac{{k}\pi}{\mathrm{15}}\right) \\ $$$$\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{14}} }=\left(\underset{\mathrm{1}} {\overset{\mathrm{7}} {\prod}}{cos}\left(\frac{{k}\pi}{\mathrm{15}}\right)\right)^{\mathrm{2}} \\ $$$$\Rightarrow\underset{{k}.\mathrm{1}} {\overset{\mathrm{7}} {\prod}}{cos}\left(\frac{{k}\pi}{\mathrm{15}}\right)=\underset{−} {+}\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{7}} },\forall{k}\in\left[\mathrm{1},\mathrm{7}\right]\cap\mathbb{N}\:\mathrm{0}\leqslant\frac{{k}\pi}{\mathrm{15}}\leqslant\frac{\pi}{\mathrm{2}} \\ $$$${cos}\left(\frac{{k}\pi}{\mathrm{15}}\right)\geqslant\mathrm{0}\Rightarrow{P}=\frac{\mathrm{1}}{\mathrm{128}} \\ $$
