Question and Answers Forum

All Questions   Topic List

OthersQuestion and Answers: Page 96

Question Number 58276    Answers: 0   Comments: 0

Question Number 58245    Answers: 1   Comments: 0

if log(a+b+c)=loga+logb+logc prove log(((2a)/(1−a^2 ))+((2b)/(1−b^2 ))+((2c)/(1−c^2 )))=log(((2a)/(1−a^2 )))+log(((2b)/(1−b^2 )))+log(((2c)/(1−c^2 )))

$${if}\:{log}\left({a}+{b}+{c}\right)={loga}+{logb}+{logc} \\ $$$${prove} \\ $$$${log}\left(\frac{\mathrm{2}{a}}{\mathrm{1}−{a}^{\mathrm{2}} }+\frac{\mathrm{2}{b}}{\mathrm{1}−{b}^{\mathrm{2}} }+\frac{\mathrm{2}{c}}{\mathrm{1}−{c}^{\mathrm{2}} }\right)={log}\left(\frac{\mathrm{2}{a}}{\mathrm{1}−{a}^{\mathrm{2}} }\right)+{log}\left(\frac{\mathrm{2}{b}}{\mathrm{1}−{b}^{\mathrm{2}} }\right)+{log}\left(\frac{\mathrm{2}{c}}{\mathrm{1}−{c}^{\mathrm{2}} }\right) \\ $$

Question Number 58195    Answers: 2   Comments: 0

(1/x)+(1/y)=(3/4) (x^2 /y)+(y^2 /x)=9 find the value of x and y

$$\frac{\mathrm{1}}{\mathrm{x}}+\frac{\mathrm{1}}{\mathrm{y}}=\frac{\mathrm{3}}{\mathrm{4}} \\ $$$$\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{y}}+\frac{\mathrm{y}^{\mathrm{2}} }{\mathrm{x}}=\mathrm{9} \\ $$$$\mathrm{find}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:\mathrm{x}\:\mathrm{and}\:\mathrm{y} \\ $$

Question Number 58193    Answers: 0   Comments: 0

If z ∈ C such that R(z^n )>0 for n∈N^+ . Show that z ∈R^+ .

$$\mathrm{If}\:{z}\:\in\:\mathbb{C}\:\:\mathrm{such}\:\mathrm{that}\:\mathfrak{R}\left({z}^{{n}} \right)>\mathrm{0}\:\mathrm{for}\:{n}\in\mathbb{N}^{+} . \\ $$$$\mathrm{Show}\:\mathrm{that}\:{z}\:\in\mathbb{R}^{+} . \\ $$

Question Number 58171    Answers: 1   Comments: 0

a particle of mass m kg is moving along a smooth wire that is fixed in a plane. The polar equation of the wire is r = ae^(3θ) . The particle moves with a cons tant velocity of 6. At time t = 0 , the par ticle is at the point with polar equation (a,θ) a)Find the transverse and radial compo nents of the acceleration of the particle in terms of a and t. b) the resultant force on the particle is F. Show that the magnitude of F at time t is 360mae^(18t)

$$\mathrm{a}\:\mathrm{particle}\:\mathrm{of}\:\mathrm{mass}\:\mathrm{m}\:\mathrm{kg}\:\mathrm{is}\:\mathrm{moving}\:\mathrm{along} \\ $$$$\mathrm{a}\:\mathrm{smooth}\:\mathrm{wire}\:\mathrm{that}\:\mathrm{is}\:\mathrm{fixed}\:\mathrm{in}\:\mathrm{a}\:\mathrm{plane}. \\ $$$$\mathrm{The}\:\mathrm{polar}\:\mathrm{equation}\:\mathrm{of}\:\mathrm{the}\:\mathrm{wire}\:\:\mathrm{is}\: \\ $$$$\mathrm{r}\:=\:\mathrm{ae}^{\mathrm{3}\theta} .\:\mathrm{The}\:\mathrm{particle}\:\mathrm{moves}\:\mathrm{with}\:\mathrm{a}\:\mathrm{cons} \\ $$$$\mathrm{tant}\:\mathrm{velocity}\:\mathrm{of}\:\mathrm{6}.\:\mathrm{At}\:\mathrm{time}\:\:\mathrm{t}\:=\:\mathrm{0}\:,\:\mathrm{the}\:\mathrm{par} \\ $$$$\mathrm{ticle}\:\mathrm{is}\:\mathrm{at}\:\mathrm{the}\:\mathrm{point}\:\mathrm{with}\:\mathrm{polar}\:\mathrm{equation} \\ $$$$\left(\mathrm{a},\theta\right) \\ $$$$\left.\mathrm{a}\right)\mathrm{Find}\:\mathrm{the}\:\mathrm{transverse}\:\mathrm{and}\:\mathrm{radial}\:\mathrm{compo} \\ $$$$\mathrm{nents}\:\mathrm{of}\:\mathrm{the}\:\mathrm{acceleration}\:\mathrm{of}\:\mathrm{the}\:\mathrm{particle} \\ $$$$\mathrm{in}\:\mathrm{terms}\:\mathrm{of}\:\mathrm{a}\:\mathrm{and}\:\mathrm{t}. \\ $$$$\left.\mathrm{b}\right)\:\mathrm{the}\:\mathrm{resultant}\:\mathrm{force}\:\mathrm{on}\:\mathrm{the}\:\mathrm{particle}\:\mathrm{is} \\ $$$$\mathrm{F}.\:\mathrm{Show}\:\mathrm{that}\:\mathrm{the}\:\mathrm{magnitude}\:\mathrm{of}\:\mathrm{F}\:\mathrm{at}\:\mathrm{time} \\ $$$$\mathrm{t}\:\mathrm{is}\:\mathrm{360mae}^{\mathrm{18t}} \\ $$

Question Number 58091    Answers: 2   Comments: 0

27x^(3−1=0)

$$\mathrm{27}{x}^{\mathrm{3}−\mathrm{1}=\mathrm{0}} \\ $$

Question Number 57953    Answers: 0   Comments: 0

It is requested to all who post question...pls 1)post physics question with diagram. 2)pls post geometry/co ordinate geometry queztions with diagram as mentioned in source. 3)pls post question in details as mentioned in the source. 4)pls post question along with the answer not in details but the answer only.

$${It}\:{is}\:{requested}\:{to}\:{all}\:{who}\:{post}\:{question}...{pls} \\ $$$$ \\ $$$$\left.\mathrm{1}\right){post}\:{physics}\:{question}\:{with}\:{diagram}. \\ $$$$\left.\mathrm{2}\right){pls}\:{post}\:{geometry}/{co}\:{ordinate}\:{geometry}\:{queztions} \\ $$$${with}\:{diagram}\:{as}\:{mentioned}\:{in}\:{source}. \\ $$$$\left.\mathrm{3}\right){pls}\:{post}\:{question}\:{in}\:{details}\:{as}\:{mentioned} \\ $$$$\:{in}\:{the}\:{source}. \\ $$$$\left.\mathrm{4}\right){pls}\:{post}\:{question}\:{along}\:{with}\:{the}\:{answer}\:{not} \\ $$$${in}\:{details}\:{but}\:{the}\:{answer}\:{only}. \\ $$$$ \\ $$

Question Number 57938    Answers: 0   Comments: 0

Question Number 57931    Answers: 0   Comments: 0

What is 2^3 +6×4

$$\mathrm{What}\:\mathrm{is}\:\mathrm{2}^{\mathrm{3}} +\mathrm{6}×\mathrm{4} \\ $$

Question Number 57873    Answers: 1   Comments: 1

If α + β+ γ =180°, show that cos (α/2) + cos (β/2)+ cos (γ/2) = 4 cos ((β + γ)/4) cos ((γ + α)/4) cos ((α + β)/4).

$$\mathrm{If}\:\alpha\:+\:\beta+\:\gamma\:=\mathrm{180}°,\:\mathrm{show}\:\mathrm{that}\:\mathrm{cos}\:\frac{\alpha}{\mathrm{2}}\:+\:\mathrm{cos}\:\frac{\beta}{\mathrm{2}}+\:\mathrm{cos}\:\frac{\gamma}{\mathrm{2}}\:=\:\mathrm{4}\:\mathrm{cos}\:\frac{\beta\:+\:\gamma}{\mathrm{4}}\:\:\mathrm{cos}\:\frac{\gamma\:+\:\alpha}{\mathrm{4}}\:\mathrm{cos}\:\frac{\alpha\:+\:\beta}{\mathrm{4}}. \\ $$

Question Number 57840    Answers: 0   Comments: 0

A uniform rod ABC, weight 50N and length 4m rests with one end A on rough horizontal ground and is supported by a smooth peg at B where AB=2.5m. The peg is 2m from the ground. Find the reactions at A and at the peg.

$$\mathrm{A}\:\mathrm{uniform}\:\mathrm{rod}\:\mathrm{ABC},\:\mathrm{weight}\:\mathrm{50N}\:\mathrm{and}\: \\ $$$$\mathrm{length}\:\mathrm{4m}\:\mathrm{rests}\:\mathrm{with}\:\mathrm{one}\:\mathrm{end}\:\mathrm{A}\:\mathrm{on}\:\mathrm{rough} \\ $$$$\mathrm{horizontal}\:\mathrm{ground}\:\mathrm{and}\:\mathrm{is}\:\mathrm{supported}\:\mathrm{by}\: \\ $$$$\mathrm{a}\:\mathrm{smooth}\:\mathrm{peg}\:\mathrm{at}\:\mathrm{B}\:\mathrm{where}\:\mathrm{AB}=\mathrm{2}.\mathrm{5m}. \\ $$$$\mathrm{The}\:\mathrm{peg}\:\mathrm{is}\:\mathrm{2m}\:\mathrm{from}\:\mathrm{the}\:\mathrm{ground}.\:\mathrm{Find}\:\mathrm{the} \\ $$$$\mathrm{reactions}\:\mathrm{at}\:\mathrm{A}\:\mathrm{and}\:\mathrm{at}\:\mathrm{the}\:\mathrm{peg}. \\ $$

Question Number 57839    Answers: 0   Comments: 0

A uniform rod AB, 3m long and weght 120N, rests in equilibrium with end A on a rough horizontal table and supported by a force P applied at its end B at right angles to the rod. The rod makes an angle of 3o° with the table. Find the force P, and the reaction at the floor.

$$\mathrm{A}\:\mathrm{uniform}\:\mathrm{rod}\:\mathrm{AB},\:\mathrm{3m}\:\mathrm{long}\:\mathrm{and}\:\mathrm{weght} \\ $$$$\mathrm{120N},\:\mathrm{rests}\:\mathrm{in}\:\mathrm{equilibrium}\:\mathrm{with}\:\mathrm{end}\:\mathrm{A} \\ $$$$\mathrm{on}\:\mathrm{a}\:\mathrm{rough}\:\mathrm{horizontal}\:\mathrm{table}\:\mathrm{and}\:\mathrm{supported}\: \\ $$$$\mathrm{by}\:\mathrm{a}\:\mathrm{force}\:\mathrm{P}\:\mathrm{applied}\:\mathrm{at}\:\mathrm{its}\:\mathrm{end}\:\mathrm{B}\:\mathrm{at}\:\mathrm{right} \\ $$$$\mathrm{angles}\:\mathrm{to}\:\mathrm{the}\:\mathrm{rod}.\:\mathrm{The}\:\mathrm{rod}\:\mathrm{makes}\:\mathrm{an}\:\mathrm{angle} \\ $$$$\mathrm{of}\:\mathrm{3o}°\:\mathrm{with}\:\mathrm{the}\:\mathrm{table}.\:\mathrm{Find}\:\mathrm{the}\:\mathrm{force}\:\mathrm{P}, \\ $$$$\mathrm{and}\:\mathrm{the}\:\mathrm{reaction}\:\mathrm{at}\:\mathrm{the}\:\mathrm{floor}. \\ $$

Question Number 57779    Answers: 0   Comments: 0

kno_3 ⇒k_2 o+n_2 +o_2

$${kno}_{\mathrm{3}} \Rightarrow{k}_{\mathrm{2}} {o}+{n}_{\mathrm{2}} +{o}_{\mathrm{2}} \\ $$

Question Number 57735    Answers: 2   Comments: 0

Question Number 57719    Answers: 1   Comments: 0

Find all complex number z that satisfy sinh z = i

$$\mathrm{Find}\:\mathrm{all}\:\mathrm{complex}\:\mathrm{number}\:{z}\:\mathrm{that}\:\mathrm{satisfy} \\ $$$$\mathrm{sinh}\:{z}\:=\:{i} \\ $$

Question Number 57619    Answers: 2   Comments: 0

Question Number 57618    Answers: 1   Comments: 0

Question Number 57617    Answers: 3   Comments: 1

Question Number 57601    Answers: 2   Comments: 1

Question Number 57599    Answers: 2   Comments: 0

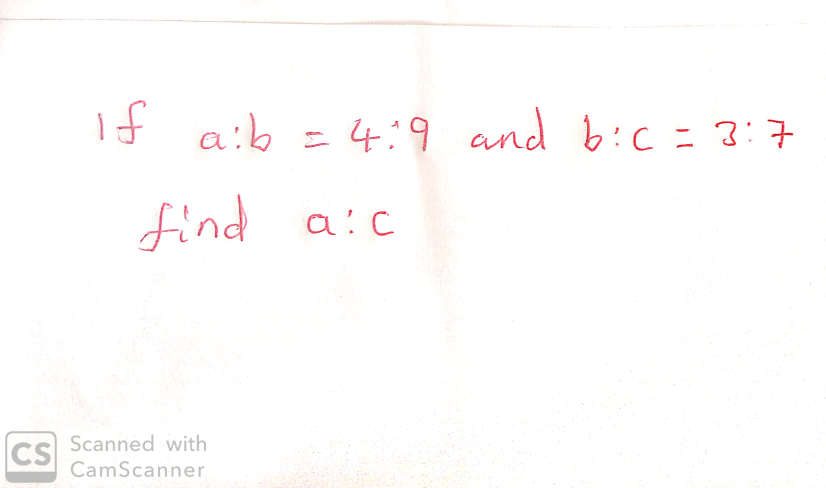
Question Number 57491    Answers: 1   Comments: 0

If R is a region enclosed by y = f(x), y = g(x), x = a, x = b, is it possible to have f(x) and g(x) such that the center of gravity (x^ , y^ ) is not inside R ?

$$\mathrm{If}\:{R}\:\mathrm{is}\:\mathrm{a}\:\mathrm{region}\:\mathrm{enclosed}\:\mathrm{by}\:{y}\:=\:{f}\left({x}\right),\:{y}\:=\:{g}\left({x}\right),\:{x}\:=\:{a},\:{x}\:=\:{b}, \\ $$$$\mathrm{is}\:\mathrm{it}\:\mathrm{possible}\:\mathrm{to}\:\mathrm{have}\:{f}\left({x}\right)\:\mathrm{and}\:{g}\left({x}\right)\:\mathrm{such}\:\mathrm{that} \\ $$$$\mathrm{the}\:\mathrm{center}\:\mathrm{of}\:\mathrm{gravity}\:\left(\bar {{x}},\:\bar {{y}}\right)\:\mathrm{is}\:\mathrm{not}\:\mathrm{inside}\:{R}\:? \\ $$

Question Number 57405    Answers: 1   Comments: 0

calculate lim_(x→0) ((1−cosx.cos(2x)....cos(nx))/x^2 ) with n integr natural not 0.

$${calculate}\:{lim}_{{x}\rightarrow\mathrm{0}} \frac{\mathrm{1}−{cosx}.{cos}\left(\mathrm{2}{x}\right)....{cos}\left({nx}\right)}{{x}^{\mathrm{2}} } \\ $$$${with}\:{n}\:{integr}\:{natural}\:{not}\:\mathrm{0}. \\ $$

Question Number 57348    Answers: 1   Comments: 2

Question Number 57309    Answers: 0   Comments: 0

Question Number 57284    Answers: 1   Comments: 1

y is varies directly as the square of x and inversely as z. if x is inceased by 10% and z is decreased by 20%, find the percentage change in y.

$${y}\:{is}\:{varies}\:{directly}\:{as}\:{the}\:{square}\:{of}\:{x}\:{and} \\ $$$${inversely}\:{as}\:{z}. \\ $$$${if}\:{x}\:{is}\:{inceased}\:{by}\:\mathrm{10\%}\:{and}\:{z}\:\:{is}\: \\ $$$${decreased}\:{by}\:\mathrm{20\%},\:{find}\:{the}\:{percentage} \\ $$$${change}\:{in}\:{y}. \\ $$

Question Number 57184    Answers: 2   Comments: 1

  Pg 91      Pg 92      Pg 93      Pg 94      Pg 95      Pg 96      Pg 97      Pg 98      Pg 99      Pg 100   

Terms of Service

Privacy Policy

Contact: info@tinkutara.com