Question and Answers Forum

OthersQuestion and Answers: Page 91

Question Number 64017 Answers: 0 Comments: 4

why can′t we differentiate or intergrate powers of trigonometric functions such as 1) ∫cos^2 xdx? 3) ∫tan^2 2xdx 2)∫sin^2 xdx? 4) ∫sin^(10) x hence how do we solve such problems.?

$${why}\:{can}'{t}\:{we}\:{differentiate}\:{or}\:{intergrate}\:{powers}\:{of}\:{trigonometric} \\ $$$${functions}\:{such}\:{as}\: \\ $$$$\left.\mathrm{1}\left.\right)\:\int{cos}^{\mathrm{2}} {xdx}?\:\:\:\:\mathrm{3}\right)\:\int{tan}^{\mathrm{2}} \mathrm{2}{xdx} \\ $$$$\left.\mathrm{2}\left.\right)\int{sin}^{\mathrm{2}} {xdx}?\:\:\:\:\:\mathrm{4}\right)\:\int{sin}^{\mathrm{10}} {x} \\ $$$${hence}\:{how}\:{do}\:{we}\:{solve}\:{such}\:{problems}.? \\ $$

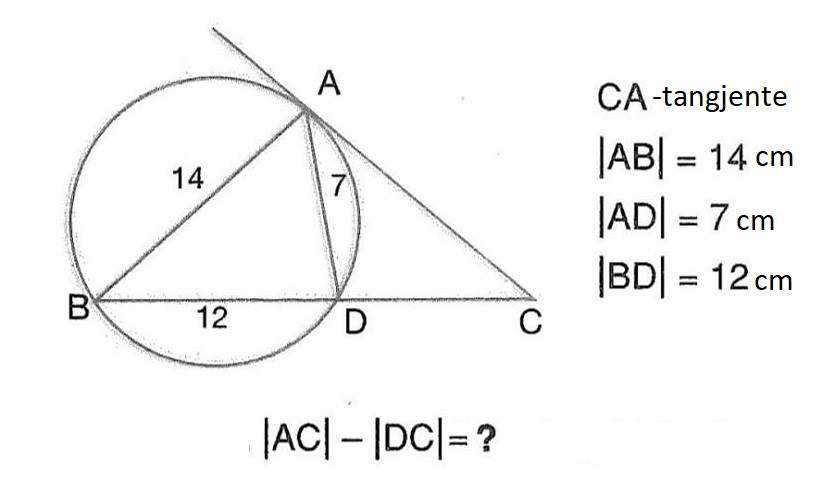
Question Number 64015 Answers: 1 Comments: 0

How can such questions be solved.? x^2 −∣7∣ +10=0 x^2 −∣x∣−6>0

$$\:{How}\:{can}\:{such}\:{questions}\:{be}\:{solved}.? \\ $$$$\:\:{x}^{\mathrm{2}} −\mid\mathrm{7}\mid\:+\mathrm{10}=\mathrm{0} \\ $$$$\:\:{x}^{\mathrm{2}} −\mid{x}\mid−\mathrm{6}>\mathrm{0} \\ $$$$\:\: \\ $$

Question Number 63984 Answers: 1 Comments: 5

is it true? e^(lnx) = x? if so then (d/dx)(e^(lnx) )=?

$${is}\:{it}\:{true}? \\ $$$$\:\:{e}^{{lnx}} =\:{x}? \\ $$$${if}\:{so}\:{then}\:\:\frac{{d}}{{dx}}\left({e}^{{lnx}} \right)=? \\ $$

Question Number 63983 Answers: 1 Comments: 0

Please i need someones help on this How do i find an Asymptote to a curve? and also how find a general solution for a differential equation.

$${Please}\:{i}\:{need}\:{someones}\:{help}\:{on}\:{this}\: \\ $$$${How}\:{do}\:{i}\:{find}\:{an}\:{Asymptote}\:{to}\:{a}\:{curve}? \\ $$$${and}\:{also}\:{how}\:{find}\:{a}\:{general}\:{solution}\:{for}\:{a}\:{differential}\: \\ $$$${equation}. \\ $$$$ \\ $$

Question Number 63891 Answers: 0 Comments: 0

A bus is travelling along a straight road at 100Km/hr and the bus conductor walks at 6Km/hr on the floor of the bus and in the same direction as the bus. Find the speed of the conductor relative to the road, and relative to the bus. If the bus conductor now works at the same rate but in the opposite direction as the bus, find his new speed relative to the road. Answers in textbook: 106Km/hr, 64Km/hr, 94Km/hr

Question Number 63812 Answers: 0 Comments: 2

A can terminate a work 9 hour earlier than B. A and B terminate that work after 20 hour together. A can terminate that work after .... hour.

$$ \\ $$$${A}\:\:{can}\:{terminate}\:{a}\:{work}\:\:\mathrm{9}\:{hour}\:{earlier} \\ $$$${than}\:{B}. \\ $$$${A}\:\:{and}\:\:{B}\:\:{terminate}\:{that}\:{work}\:\:{after}\:\mathrm{20}\:{hour}\:{together}. \\ $$$${A}\:{can}\:{terminate}\:{that}\:{work}\:{after}\:....\:{hour}. \\ $$$$ \\ $$$$ \\ $$

Question Number 63758 Answers: 0 Comments: 6

Tanmay Sir. Are you ok ?

$$\mathrm{Tanmay}\:\mathrm{Sir}.\:\mathrm{Are}\:\mathrm{you}\:\mathrm{ok}\:? \\ $$

Question Number 63790 Answers: 2 Comments: 0

Question Number 63789 Answers: 0 Comments: 0

Question Number 63788 Answers: 1 Comments: 0

Question Number 63700 Answers: 0 Comments: 0

Question Number 63689 Answers: 0 Comments: 3

Show that if a∣b then an∣bn

$${Show}\:{that}\:\:{if}\:\:{a}\mid{b}\:\:{then}\:{an}\mid{bn} \\ $$

Question Number 63684 Answers: 0 Comments: 0

cot 118

$$\mathrm{cot}\:\mathrm{118} \\ $$

Question Number 63552 Answers: 1 Comments: 1

Calculate ∫_0 ^(1/2) x(√(x^2 +1)) dx+∫_(1/2) ^1 x^2 (√(x^3 +1)) dx+∫_1 ^2 x^3 (√(x^4 +1)) dx+∫_2 ^3 x^4 (√(x^5 +1 ))dx+...+∫_(78) ^(79) x^(80) (√(x^(81) +1)) dx+∫_(79) ^(80) x^(81) (√(x^(82) +1)) dx usingΣ_(n=2) ^(80) ∫_(n−1) ^n x^(n+1) (√(x^(n+2) +1))dx

$${Calculate}\:\underset{\mathrm{0}} {\overset{\frac{\mathrm{1}}{\mathrm{2}}} {\int}}{x}\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}\:{dx}+\underset{\frac{\mathrm{1}}{\mathrm{2}}} {\overset{\mathrm{1}} {\int}}{x}^{\mathrm{2}} \sqrt{{x}^{\mathrm{3}} +\mathrm{1}}\:{dx}+\underset{\mathrm{1}} {\overset{\mathrm{2}} {\int}}{x}^{\mathrm{3}} \sqrt{{x}^{\mathrm{4}} +\mathrm{1}}\:{dx}+\underset{\mathrm{2}} {\overset{\mathrm{3}} {\int}}{x}^{\mathrm{4}} \sqrt{{x}^{\mathrm{5}} +\mathrm{1}\:}{dx}+...+\underset{\mathrm{78}} {\overset{\mathrm{79}} {\int}}{x}^{\mathrm{80}} \sqrt{{x}^{\mathrm{81}} +\mathrm{1}}\:{dx}+\underset{\mathrm{79}} {\overset{\mathrm{80}} {\int}}{x}^{\mathrm{81}} \sqrt{{x}^{\mathrm{82}} +\mathrm{1}}\:{dx} \\ $$$${using}\underset{{n}=\mathrm{2}} {\overset{\mathrm{80}} {\sum}}\underset{{n}−\mathrm{1}} {\overset{{n}} {\int}}{x}^{{n}+\mathrm{1}} \sqrt{{x}^{{n}+\mathrm{2}} +\mathrm{1}}{dx} \\ $$

Question Number 63534 Answers: 1 Comments: 0

find the set of values of x for which y is real if y=(((x−2)(x−1))/(x+2)) , x≠−2, x∈R

$${find}\:{the}\:{set}\:{of}\:{values}\:{of}\:{x}\:{for}\:{which}\:{y}\:{is}\:{real}\:{if}\: \\ $$$$\:{y}=\frac{\left({x}−\mathrm{2}\right)\left({x}−\mathrm{1}\right)}{{x}+\mathrm{2}}\:,\:{x}\neq−\mathrm{2},\:{x}\in\mathbb{R} \\ $$

Question Number 63532 Answers: 1 Comments: 0

prove that there exist unique intergers p and s sucb that a = bp + s with −((∣b∣)/2)< s ≤((∣b∣)/2) hence find p and s given that a=49 and b=26

$${prove}\:{that}\:{there}\:{exist}\:{unique}\:{intergers}\:{p}\:{and}\:{s}\:{sucb}\:{that} \\ $$$${a}\:=\:{bp}\:+\:{s}\:{with}\:−\frac{\mid{b}\mid}{\mathrm{2}}<\:{s}\:\leqslant\frac{\mid{b}\mid}{\mathrm{2}} \\ $$$${hence}\:{find}\:{p}\:{and}\:{s}\:{given}\:{that}\:{a}=\mathrm{49}\:{and}\:{b}=\mathrm{26} \\ $$

Question Number 63517 Answers: 1 Comments: 0

Given that ∣z−6∣=2∣z+6−9i∣, a) Use algebra to show that the locus of z is a circle, stating its center and its radius. b) sketch the locus z on an argand diagram.

$$\mathrm{Given}\:\mathrm{that}\:\:\mid{z}−\mathrm{6}\mid=\mathrm{2}\mid{z}+\mathrm{6}−\mathrm{9}{i}\mid, \\ $$$$\left.\mathrm{a}\right)\:\mathrm{Use}\:\mathrm{algebra}\:\mathrm{to}\:\mathrm{show}\:\mathrm{that}\:\mathrm{the}\:\mathrm{locus}\:\mathrm{of}\:{z}\:\mathrm{is}\:\mathrm{a}\:\mathrm{circle}, \\ $$$$\mathrm{stating}\:\mathrm{its}\:\mathrm{center}\:\mathrm{and}\:\mathrm{its}\:\mathrm{radius}. \\ $$$$\left.\mathrm{b}\right)\:\mathrm{sketch}\:\mathrm{the}\:\mathrm{locus}\:{z}\:\mathrm{on}\:\mathrm{an}\:\mathrm{argand}\:\mathrm{diagram}. \\ $$

Question Number 63507 Answers: 1 Comments: 0

let U_n =∫_(1/n) ^1 ((√(x^2 +x+1)) −(√(x^2 −x+1)))dx (n>0) 1)calculate lim_(n→+∞) U_n 2) find nature of Σ U_n

$${let}\:{U}_{{n}} =\int_{\frac{\mathrm{1}}{{n}}} ^{\mathrm{1}} \left(\sqrt{{x}^{\mathrm{2}} +{x}+\mathrm{1}}\:−\sqrt{{x}^{\mathrm{2}} −{x}+\mathrm{1}}\right){dx}\:\:\:\left({n}>\mathrm{0}\right) \\ $$$$\left.\mathrm{1}\right){calculate}\:{lim}_{{n}\rightarrow+\infty} \:\:{U}_{{n}} \\ $$$$\left.\mathrm{2}\right)\:\:{find}\:{nature}\:{of}\:\:\Sigma\:{U}_{{n}} \\ $$

Question Number 63499 Answers: 1 Comments: 0

given that a∣b, show that −a∣b.

$${given}\:{that}\:\:\:{a}\mid{b},\:{show}\:{that}\:−{a}\mid{b}. \\ $$

Question Number 63447 Answers: 1 Comments: 2

How to calculate ⌈(n) using gamma function ∀n∈R

$${How}\:{to}\:{calculate}\:\lceil\left({n}\right)\: \\ $$$${using}\:{gamma}\:{function} \\ $$$$\forall{n}\in{R} \\ $$

Question Number 63428 Answers: 0 Comments: 2

It is given that S_n =Σ_(r=1) ^n (3r^(2 ) −3r−1). Use the the formulae of Σ_(r=1) ^n r^(2 ) and Σ_(r=1) ^n r to show that S_n =n^3 . sir Forkum Michael

$${It}\:{is}\:{given}\:{that}\:{S}_{{n}} =\underset{{r}=\mathrm{1}} {\overset{{n}} {\sum}}\left(\mathrm{3}{r}^{\mathrm{2}\:} −\mathrm{3}{r}−\mathrm{1}\right).\:{Use}\:{the}\:{the}\:{formulae} \\ $$$${of}\:\underset{{r}=\mathrm{1}} {\overset{{n}} {\sum}}{r}^{\mathrm{2}\:\:} {and}\:\underset{{r}=\mathrm{1}} {\overset{{n}} {\sum}}{r}\:\:{to}\:{show}\:{that}\:{S}_{{n}} ={n}^{\mathrm{3}} . \\ $$$${sir}\:{Forkum}\:{Michael} \\ $$

Question Number 63425 Answers: 0 Comments: 0

The probability that a vaccinated person(V) contracts a disease is (1/(20)). For a person vaccinated(V ′) , the probability of contracting a disease is (5/6). In a certain town 90%of thepopulation has been vaccinated against a disease. A person is selected at random from the town,find the probability that: (a) he has the disease, (b) he is vaccinated or he has the disease. sir Forkum Michael

$${The}\:{probability}\:{that}\:{a}\:{vaccinated}\:{person}\left({V}\right)\:{contracts}\:{a}\:{disease} \\ $$$${is}\:\frac{\mathrm{1}}{\mathrm{20}}.\:{For}\:{a}\:{person}\:{vaccinated}\left({V}\:'\right)\:,\:{the}\:{probability}\:{of}\:{contracting} \\ $$$${a}\:{disease}\:{is}\:\frac{\mathrm{5}}{\mathrm{6}}.\:{In}\:{a}\:{certain}\:{town}\:\mathrm{90\%}{of}\:{thepopulation}\:{has} \\ $$$${been}\:{vaccinated}\:{against}\:{a}\:{disease}.\:{A}\:{person}\:{is}\:{selected}\:{at} \\ $$$${random}\:{from}\:{the}\:{town},{find}\:{the}\:{probability}\:{that}: \\ $$$$\left({a}\right)\:{he}\:{has}\:{the}\:{disease}, \\ $$$$\left({b}\right)\:{he}\:{is}\:{vaccinated}\:{or}\:{he}\:{has}\:{the}\:{disease}. \\ $$$${sir}\:{Forkum}\:{Michael} \\ $$

Question Number 63424 Answers: 0 Comments: 0

A colony of bacteria if left undisturbed will grow at a rate proportional to the number of bacteria, P present at time,t. However,a toxic substance is being added slowly such that at time t, the bacteria also die at the rate μPt where μ is a positive constant. (a) Show that at time t the rate of growth of the bacteria in the colony is governed by the differential equation (dP/dt)= (k−μt)p where k is apositive constant. when t=0, (dP/dt)=2P and when t=1, (dP/dt)=((19)/(10))P (b) show that (dP/dt)= (1/(10))(20−t)P. Sir Forkum Michael.

$${A}\:{colony}\:{of}\:{bacteria}\:{if}\:{left}\:{undisturbed}\:{will}\:{grow}\:{at}\:{a}\:{rate} \\ $$$${proportional}\:{to}\:{the}\:{number}\:{of}\:{bacteria},\:{P}\:{present}\:{at}\:{time},{t}. \\ $$$${However},{a}\:{toxic}\:{substance}\:{is}\:{being}\:{added}\:{slowly}\:{such}\:{that} \\ $$$${at}\:{time}\:{t},\:{the}\:{bacteria}\:{also}\:{die}\:{at}\:{the}\:{rate}\:\mu{Pt}\:{where}\:\mu\:{is} \\ $$$${a}\:{positive}\:{constant}. \\ $$$$\left({a}\right)\:\:{Show}\:{that}\:{at}\:{time}\:{t}\:{the}\:{rate}\:{of}\:{growth}\:{of}\:{the}\:{bacteria}\:{in} \\ $$$${the}\:{colony}\:{is}\:{governed}\:{by}\:{the}\:{differential}\:{equation} \\ $$$$\:\frac{{dP}}{{dt}}=\:\left({k}−\mu{t}\right){p}\:{where}\:{k}\:{is}\:{apositive}\:{constant}. \\ $$$${when}\:{t}=\mathrm{0},\:\frac{{dP}}{{dt}}=\mathrm{2}{P}\:{and}\:{when}\:{t}=\mathrm{1},\:\frac{{dP}}{{dt}}=\frac{\mathrm{19}}{\mathrm{10}}{P} \\ $$$$\left({b}\right)\:{show}\:{that}\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{{dP}}{{dt}}=\:\frac{\mathrm{1}}{\mathrm{10}}\left(\mathrm{20}−{t}\right){P}. \\ $$$$\:{Sir}\:{Forkum}\:{Michael}. \\ $$

Question Number 63296 Answers: 1 Comments: 1

A random Variable Y has probability function P, defined by P(y) = { (((y^2 /k) , y= 1,2,3)),(((((y−7)^2 )/k) , y= 4,5,6)),((0 , otherwise.)) :} Find (i) The value of the constant k. (ii) the mean and varriance of Y. (iii) The variance R, where R= 2Y −3.

$${A}\:{random}\:{Variable}\:{Y}\:{has}\:{probability}\:{function}\:{P},\:{defined}\:{by} \\ $$$$\:{P}\left({y}\right)\:=\:\begin{cases}{\frac{{y}^{\mathrm{2}} }{{k}}\:,\:{y}=\:\mathrm{1},\mathrm{2},\mathrm{3}}\\{\frac{\left({y}−\mathrm{7}\right)^{\mathrm{2}} }{{k}}\:,\:{y}=\:\mathrm{4},\mathrm{5},\mathrm{6}}\\{\mathrm{0}\:\:\:\:,\:{otherwise}.}\end{cases} \\ $$$${Find}\: \\ $$$$\left({i}\right)\:{The}\:{value}\:{of}\:{the}\:{constant}\:{k}. \\ $$$$\left({ii}\right)\:{the}\:{mean}\:{and}\:{varriance}\:{of}\:{Y}. \\ $$$$\left({iii}\right)\:{The}\:{variance}\:{R},\:{where}\:{R}=\:\mathrm{2}{Y}\:−\mathrm{3}. \\ $$

Question Number 63267 Answers: 0 Comments: 3

lim_(n→∞) (((n^3 + 1)/(n^3 − 1)))^(2n − n^3 )

$$\:\:\:\:\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\:\:\left(\frac{\mathrm{n}^{\mathrm{3}} \:+\:\mathrm{1}}{\mathrm{n}^{\mathrm{3}} \:−\:\mathrm{1}}\right)^{\mathrm{2n}\:−\:\mathrm{n}^{\mathrm{3}} } \\ $$

Question Number 63288 Answers: 1 Comments: 0

Pg 86 Pg 87 Pg 88 Pg 89 Pg 90 Pg 91 Pg 92 Pg 93 Pg 94 Pg 95

Contact: info@tinkutara.com