Question and Answers Forum

OthersQuestion and Answers: Page 85

Question Number 69104 Answers: 0 Comments: 3

Question Number 69098 Answers: 1 Comments: 3

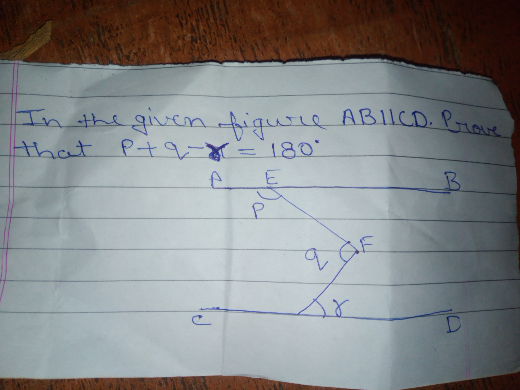
Question Number 69014 Answers: 1 Comments: 0

a) ∫∣ x^2 +2x + 1∣dx b) ∫_0 ^4 ∣x^2 +3x−2∣dx

$$\left.{a}\right)\:\:\:\int\mid\:{x}^{\mathrm{2}} +\mathrm{2}{x}\:+\:\mathrm{1}\mid{dx} \\ $$$$\left.{b}\right)\:\int_{\mathrm{0}} ^{\mathrm{4}} \mid{x}^{\mathrm{2}} +\mathrm{3}{x}−\mathrm{2}\mid{dx} \\ $$

Question Number 69010 Answers: 0 Comments: 8

To Tinku Tara, The Developer Sir, You′re going to update this, useful in real sense, precious app. Taking advantage of this opportunity I suggest some revolutionary changes if they′re possible for you. •HIDE/UNHIDE DETALS. It′s very useful to hide some details of an answer for authers in order to offer overall view.If the reader wants these details they can unhide these by clicking some symbol(small triangles etc).Can we expect this feature? •HYPERLINK FACILITY. Some posts contain reference to some other questions.Is it possible to make these question numbers hyperlinks in order to reach these questions directly and come back? •REPLACING A SYMBOL BY AN EXPRESSION. At sometimes the auther needs to replace some symbol/expression by an other symbol/expression in whole document or some portion of it. Pl consider this if it′s not very difficult for you. Forum-friends can request some other features.

$${To}\:{Tinku}\:{Tara},\:{The}\:{Developer} \\ $$$${Sir}, \\ $$$$\:\:\:\:\:\:\:\:\:{You}'{re}\:{going}\:{to}\:{update}\:{this}, \\ $$$$\boldsymbol{{useful}}\:\boldsymbol{{in}}\:\boldsymbol{{real}}\:\boldsymbol{{sense}},\:{precious}\:{app}. \\ $$$${Taking}\:{advantage}\:{of}\:{this}\:{opportunity} \\ $$$${I}\:{suggest}\:{some}\:{revolutionary}\: \\ $$$${changes}\:{if}\:{they}'{re}\:{possible}\:{for}\:{you}. \\ $$$$\bullet{HIDE}/{UNHIDE}\:{DETALS}. \\ $$$${It}'{s}\:{very}\:{useful}\:{to}\:{hide}\:{some}\:{details} \\ $$$${of}\:{an}\:{answer}\:{for}\:{authers}\:{in}\:{order}\:{to}\: \\ $$$${offer}\:{overall}\:{view}.{If}\:{the}\:{reader} \\ $$$${wants}\:{these}\:{details}\:{they}\:{can}\:{unhide} \\ $$$${these}\:{by}\:{clicking}\:{some}\:{symbol}\left({small}\right. \\ $$$$\left.{triangles}\:{etc}\right).{Can}\:{we}\:{expect}\:{this} \\ $$$${feature}? \\ $$$$\bullet{HYPERLINK}\:{FACILITY}. \\ $$$${Some}\:{posts}\:{contain}\:{reference}\:{to} \\ $$$${some}\:{other}\:{questions}.{Is}\:{it}\:{possible} \\ $$$${to}\:{make}\:{these}\:{question}\:{numbers} \\ $$$$\boldsymbol{{hyperlinks}}\:{in}\:{order}\:{to}\:{reach} \\ $$$${these}\:{questions}\:{directly}\:{and}\:{come} \\ $$$${back}? \\ $$$$\bullet{REPLACING}\:{A}\:{SYMBOL} \\ $$$$\:\:\:{BY}\:{AN}\:{EXPRESSION}. \\ $$$${At}\:{sometimes}\:{the}\:{auther}\:{needs} \\ $$$${to}\:{replace}\:{some}\:{symbol}/{expression} \\ $$$${by}\:{an}\:{other}\:{symbol}/{expression}\:{in} \\ $$$${whole}\:{document}\:{or}\:{some}\:{portion}\:{of} \\ $$$${it}.\:{Pl}\:{consider}\:{this}\:{if}\:{it}'{s}\:{not}\:{very} \\ $$$${difficult}\:{for}\:{you}. \\ $$$${Forum}-{friends}\:{can}\:{request}\:{some} \\ $$$${other}\:{features}. \\ $$

Question Number 68830 Answers: 0 Comments: 0

please can someone check question 68728

$${please}\:{can}\:{someone}\:{check}\:{question}\:\:\:\mathrm{68728} \\ $$

Question Number 68676 Answers: 0 Comments: 2

Solve the equation tanh^(−1) (((x−2)/(x+1))) = ln 2 show that the set {1,2,4,8} under ×_(15) ,multiplication mod 15 forms a group.

$${Solve}\:{the}\:{equation} \\ $$$${tanh}^{−\mathrm{1}} \left(\frac{{x}−\mathrm{2}}{{x}+\mathrm{1}}\right)\:=\:{ln}\:\mathrm{2} \\ $$$${show}\:{that}\:{the}\:{set}\:\left\{\mathrm{1},\mathrm{2},\mathrm{4},\mathrm{8}\right\}\:\:{under}\:×_{\mathrm{15}} \:,{multiplication}\:{mod}\:\mathrm{15}\:\:{forms}\:{a}\:{group}. \\ $$

Question Number 68675 Answers: 0 Comments: 3

Express in partial fraction f(x) ≡ ((2x^3 + x + 2)/((x^2 +1)(x+1)(x−2))) x ≠ −1,2 Hence or otherwise show that ∫_0 ^1 f(x) dx = −(1/(12))[ 13ln 2 + π]

$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\: \\ $$$$\:{Express}\:{in}\:{partial}\:{fraction}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\: \\ $$$$\:{f}\left({x}\right)\:\equiv\:\frac{\mathrm{2}{x}^{\mathrm{3}} \:+\:{x}\:+\:\mathrm{2}}{\left({x}^{\mathrm{2}} +\mathrm{1}\right)\left({x}+\mathrm{1}\right)\left({x}−\mathrm{2}\right)}\:{x}\:\neq\:−\mathrm{1},\mathrm{2} \\ $$$${Hence}\:{or}\:{otherwise}\:\:{show}\:{that}\:\: \\ $$$$\:\int_{\mathrm{0}} ^{\mathrm{1}} {f}\left({x}\right)\:{dx}\:=\:−\frac{\mathrm{1}}{\mathrm{12}}\left[\:\mathrm{13}{ln}\:\mathrm{2}\:+\:\pi\right] \\ $$$$ \\ $$

Question Number 68617 Answers: 0 Comments: 1

find the value of p given that 3^p × 3^(−1) × 5 × 3^(p−1) = 2 × 3^4

$${find}\:{the}\:{value}\:{of}\:{p}\:{given}\:{that} \\ $$$$\mathrm{3}^{{p}} \:×\:\mathrm{3}^{−\mathrm{1}} \:×\:\mathrm{5}\:×\:\mathrm{3}^{{p}−\mathrm{1}} \:=\:\mathrm{2}\:×\:\mathrm{3}^{\mathrm{4}} \\ $$

Question Number 68609 Answers: 1 Comments: 1

Question Number 68278 Answers: 0 Comments: 2

Question Number 67927 Answers: 0 Comments: 9

Tinku Tara,the developer. Sir, I don′t receive notifications from the forum.Pl fix the problem.

$$\mathrm{Tinku}\:\mathrm{Tara},\mathrm{the}\:\mathrm{developer}. \\ $$$$\mathrm{Sir}, \\ $$$$\mathrm{I}\:\mathrm{don}'\mathrm{t}\:\mathrm{receive}\:\mathrm{notifications}\:\mathrm{from} \\ $$$$\mathrm{the}\:\mathrm{forum}.\mathrm{Pl}\:\mathrm{fix}\:\mathrm{the}\:\mathrm{problem}. \\ $$

Question Number 67903 Answers: 2 Comments: 0

Question Number 67898 Answers: 0 Comments: 0

differential equation. homogenous. ydx+(2x+3y)dy=0

$$ \\ $$$${differential}\:{equation}. \\ $$$${homogenous}. \\ $$$$ \\ $$$${ydx}+\left(\mathrm{2}{x}+\mathrm{3}{y}\right){dy}=\mathrm{0} \\ $$$$ \\ $$

Question Number 67820 Answers: 0 Comments: 1

x^3 −x^2 −6x

$${x}^{\mathrm{3}} −{x}^{\mathrm{2}} −\mathrm{6}{x} \\ $$

Question Number 67745 Answers: 3 Comments: 0

solve the system of equations { ((3∣x−5∣+4=y)),((∣y−3∣=4x−12)) :}

$${solve}\:{the}\:{system}\:{of}\:{equations\begin{cases}{\mathrm{3}\mid{x}−\mathrm{5}\mid+\mathrm{4}={y}}\\{\mid{y}−\mathrm{3}\mid=\mathrm{4}{x}−\mathrm{12}}\end{cases}} \\ $$

Question Number 67697 Answers: 1 Comments: 0

⋓si⋒g ChineseRemainderTheorm ∂etermine polynomial p(x) such that p(x)≡8(mod x+1) p(x)≡−24(mod x+3) p(x)≡6(mod x) p(x)≡0(mod x+2)

$$\Cup\mathrm{si}\Cap\mathrm{g}\:\mathrm{ChineseRemainderTheorm} \\ $$$$\partial\mathrm{etermine}\:\mathrm{polynomial}\:\mathrm{p}\left(\mathrm{x}\right)\:\mathrm{such}\:\mathrm{that} \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\:\mathrm{p}\left(\mathrm{x}\right)\equiv\mathrm{8}\left(\mathrm{mod}\:\mathrm{x}+\mathrm{1}\right) \\ $$$$\:\:\:\:\:\:\:\:\mathrm{p}\left(\mathrm{x}\right)\equiv−\mathrm{24}\left(\mathrm{mod}\:\mathrm{x}+\mathrm{3}\right) \\ $$$$\:\:\:\:\:\:\:\:\mathrm{p}\left(\mathrm{x}\right)\equiv\mathrm{6}\left(\mathrm{mod}\:\mathrm{x}\right) \\ $$$$\:\:\:\:\:\:\:\:\mathrm{p}\left(\mathrm{x}\right)\equiv\mathrm{0}\left(\mathrm{mod}\:\mathrm{x}+\mathrm{2}\right) \\ $$$$ \\ $$

Question Number 67688 Answers: 0 Comments: 1

A relation R defined by _((x,y)) R_((u,v)) ⇔ v^2 −y^2 = u^2 −x^2 show that R is an equivalent Relation.

$${A}\:{relation}\:\mathbb{R}\:{defined}\:{by}\:\:\:_{\left({x},{y}\right)} {R}_{\left({u},{v}\right)} \:\Leftrightarrow\:\:{v}^{\mathrm{2}} −{y}^{\mathrm{2}} \:=\:{u}^{\mathrm{2}} −{x}^{\mathrm{2}} \\ $$$${show}\:{that}\:{R}\:{is}\:{an}\:{equivalent}\:{Relation}. \\ $$

Question Number 67687 Answers: 0 Comments: 3

find the range of values of ∣((x^2 −9)/3_ )∣= ((9−x^2 )/3)

$${find}\:{the}\:{range}\:{of}\:{values}\:{of}\: \\ $$$$\:\:\mid\frac{{x}^{\mathrm{2}} −\mathrm{9}}{\mathrm{3}_{\:} }\mid=\:\frac{\mathrm{9}−{x}^{\mathrm{2}} }{\mathrm{3}} \\ $$$$ \\ $$

Question Number 67686 Answers: 0 Comments: 2

given that the roots of the equation 4x^2 + 6x + 9 =0 are λ and δ where λ = (1 + α^2 +β^2 ) and δ = α^3 + β^3 find an equation whose roots are (1/(αλ)) and (1/(βδ))

$${given}\:{that}\:{the}\:{roots}\:{of}\:{the}\:{equation}\:\:\mathrm{4}{x}^{\mathrm{2}} \:+\:\mathrm{6}{x}\:+\:\mathrm{9}\:=\mathrm{0}\:{are}\:\:\lambda\:{and}\:\delta\:\:{where}\: \\ $$$$\:\lambda\:=\:\left(\mathrm{1}\:+\:\alpha^{\mathrm{2}} \:+\beta^{\mathrm{2}} \right)\:\:{and}\:\:\delta\:=\:\alpha^{\mathrm{3}} \:+\:\beta^{\mathrm{3}} \\ $$$${find}\:{an}\:{equation}\:{whose}\:{roots}\:{are}\: \\ $$$$\:\:\frac{\mathrm{1}}{\alpha\lambda}\:{and}\:\:\frac{\mathrm{1}}{\beta\delta} \\ $$

Question Number 67684 Answers: 0 Comments: 2

given the function f(x) = { ((x^2 , for 0≤ x< 2)),((ax + 3, for 2≤ x < 4)) :} is periodic of period 4, and is continuous. a) Find the value of a. b) Find the valu of f(6) c) sketch the graph for y =f(x). help me please, for the graph i don′t know wbere to put y=x^2 and y = ax + 3 and where do i put a closed dot and an open dot.

$${given}\:{the}\:{function}\: \\ $$$${f}\left({x}\right)\:=\begin{cases}{{x}^{\mathrm{2}} \:\:,\:{for}\:\:\:\mathrm{0}\leqslant\:{x}<\:\mathrm{2}}\\{{ax}\:+\:\mathrm{3},\:{for}\:\:\mathrm{2}\leqslant\:{x}\:<\:\mathrm{4}}\end{cases} \\ $$$${is}\:{periodic}\:{of}\:{period}\:\:\mathrm{4},\:{and}\:{is}\:{continuous}. \\ $$$$\left.{a}\right)\:{Find}\:\:{the}\:{value}\:{of}\:\:{a}. \\ $$$$\left.{b}\right)\:{Find}\:{the}\:{valu}\:{of}\:\:{f}\left(\mathrm{6}\right) \\ $$$$\left.{c}\right)\:{sketch}\:{the}\:{graph}\:{for}\:{y}\:={f}\left({x}\right). \\ $$$${help}\:{me}\:{please},\:{for}\:{the}\:{graph}\:{i}\:{don}'{t}\:{know}\:{wbere}\:{to}\:{put}\:\:{y}={x}^{\mathrm{2}} \:{and}\:{y}\:=\:{ax}\:+\:\mathrm{3}\:{and} \\ $$$${where}\:{do}\:{i}\:{put}\:{a}\:{closed}\:\:{dot}\:{and}\:{an}\:{open}\:{dot}. \\ $$$$ \\ $$

Question Number 67664 Answers: 0 Comments: 2

show that ∃ n ∈ N^(+ ) : sin^n x + cos^n x = 1 and cosh^n x − sinh^n x = 1. Hint: use Induction method.

$${show}\:{that}\:\:\exists\:{n}\:\in\:{N}^{+\:} \::\:\:{sin}^{{n}} {x}\:+\:{cos}^{{n}} {x}\:=\:\mathrm{1}\:{and}\:\:{cosh}^{{n}} {x}\:−\:{sinh}^{{n}} {x}\:=\:\mathrm{1}. \\ $$$$ \\ $$$${Hint}:\:{use}\:{Induction}\:{method}. \\ $$$$ \\ $$

Question Number 67662 Answers: 0 Comments: 2

please explain the fact that ∫(1/x)dx = ln x + k

$${please}\:{explain}\:{the}\:{fact}\:{that}\: \\ $$$$\int\frac{\mathrm{1}}{{x}}{dx}\:=\:{ln}\:{x}\:+\:{k} \\ $$

Question Number 67659 Answers: 0 Comments: 3

Help me obtain the value of e from (1 + (1/n))^n how do i go about it.

$${Help}\:{me}\:{obtain}\:\:\:{the}\:{value}\:{of}\:\:{e}\:{from} \\ $$$$\:\left(\mathrm{1}\:+\:\frac{\mathrm{1}}{{n}}\right)^{{n}} \:\:{how}\:{do}\:{i}\:{go}\:{about}\:{it}. \\ $$

Question Number 67631 Answers: 0 Comments: 3

Can you please tell me, where does this formula come from? And what means the factorial of a non- integer number? π = ((1/2)!)^2 × 4 I′ve verified the above equation with calculator. Thank you

$$ \\ $$$$ \\ $$$$\:\:\:\mathrm{Can}\:\mathrm{you}\:\mathrm{please}\:\mathrm{tell}\:\mathrm{me},\:\mathrm{where}\:\mathrm{does}\:\mathrm{this}\: \\ $$$$\:\:\:\mathrm{formula}\:\mathrm{come}\:\mathrm{from}? \\ $$$$\:\:\:\mathrm{And}\:\mathrm{what}\:\mathrm{means}\:\mathrm{the}\:\mathrm{factorial}\:\mathrm{of}\:\mathrm{a}\:\mathrm{non}- \\ $$$$\:\:\:\mathrm{integer}\:\mathrm{number}? \\ $$$$ \\ $$$$\:\:\:\:\:\:\pi\:=\:\left(\frac{\mathrm{1}}{\mathrm{2}}!\right)^{\mathrm{2}} ×\:\mathrm{4} \\ $$$$ \\ $$$$\:\:\:{I}'{ve}\:{verified}\:{the}\:{above}\:{equation}\:{with}\:{calculator}. \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{Thank}\:\mathrm{you} \\ $$$$ \\ $$$$ \\ $$

Question Number 67482 Answers: 0 Comments: 1

I have tried to solve Q#67299 Please see and give critical remarks

$${I}\:{have}\:{tried}\:{to}\:{solve}\:{Q}#\mathrm{67299} \\ $$$${Please}\:{see}\:{and}\:{give}\:{critical}\:{remarks} \\ $$

Question Number 67471 Answers: 0 Comments: 4

Evaluate:∫(√(x(√(x+1)))) dx

$$\boldsymbol{{Evaluate}}:\int\sqrt{{x}\sqrt{{x}+\mathrm{1}}}\:{dx} \\ $$

Pg 80 Pg 81 Pg 82 Pg 83 Pg 84 Pg 85 Pg 86 Pg 87 Pg 88 Pg 89

Contact: info@tinkutara.com