
OthersQuestion and Answers: Page 77
Question Number 81657 Answers: 0 Comments: 2
Question Number 81545 Answers: 0 Comments: 3

Question Number 81518 Answers: 0 Comments: 0

Question Number 81514 Answers: 0 Comments: 0
Question Number 81458 Answers: 0 Comments: 2
Question Number 81124 Answers: 1 Comments: 0
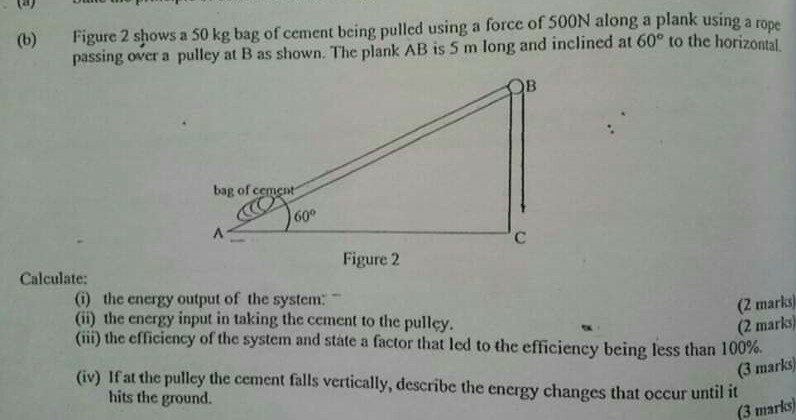
Question Number 81115 Answers: 0 Comments: 0
Question Number 80997 Answers: 0 Comments: 4
Question Number 80994 Answers: 0 Comments: 1
Question Number 80974 Answers: 0 Comments: 2
Question Number 80973 Answers: 0 Comments: 0
Question Number 80890 Answers: 1 Comments: 0
Question Number 80613 Answers: 1 Comments: 2
Question Number 80550 Answers: 1 Comments: 1

Question Number 80540 Answers: 0 Comments: 1

Question Number 80515 Answers: 0 Comments: 1
$$\int\frac{{dx}}{\left(\mathrm{1}+{x}^{\phi} \right)^{\phi} } \\ $$
Question Number 80505 Answers: 0 Comments: 8
Question Number 80504 Answers: 0 Comments: 2
Question Number 80341 Answers: 1 Comments: 0
Question Number 80340 Answers: 1 Comments: 0
Question Number 80293 Answers: 0 Comments: 12
Question Number 80175 Answers: 1 Comments: 1
$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{dx}}{\sqrt{{x}^{\mathrm{2}} +{x}+\mathrm{1}}}\:=\:? \\ $$
Question Number 80172 Answers: 0 Comments: 2
Question Number 80159 Answers: 1 Comments: 4
Question Number 80102 Answers: 0 Comments: 0

Question Number 80088 Answers: 0 Comments: 0
