
OthersQuestion and Answers: Page 76
Question Number 83202 Answers: 0 Comments: 4
Question Number 82929 Answers: 2 Comments: 0
Question Number 82886 Answers: 0 Comments: 2
Question Number 82867 Answers: 0 Comments: 3
Question Number 82729 Answers: 1 Comments: 2

Question Number 82721 Answers: 1 Comments: 2
Question Number 82639 Answers: 0 Comments: 3

Question Number 82616 Answers: 0 Comments: 0
Question Number 82583 Answers: 0 Comments: 0

Question Number 82564 Answers: 0 Comments: 0

Question Number 82497 Answers: 0 Comments: 0

Question Number 82415 Answers: 0 Comments: 1

Question Number 82387 Answers: 0 Comments: 0

Question Number 82386 Answers: 0 Comments: 0
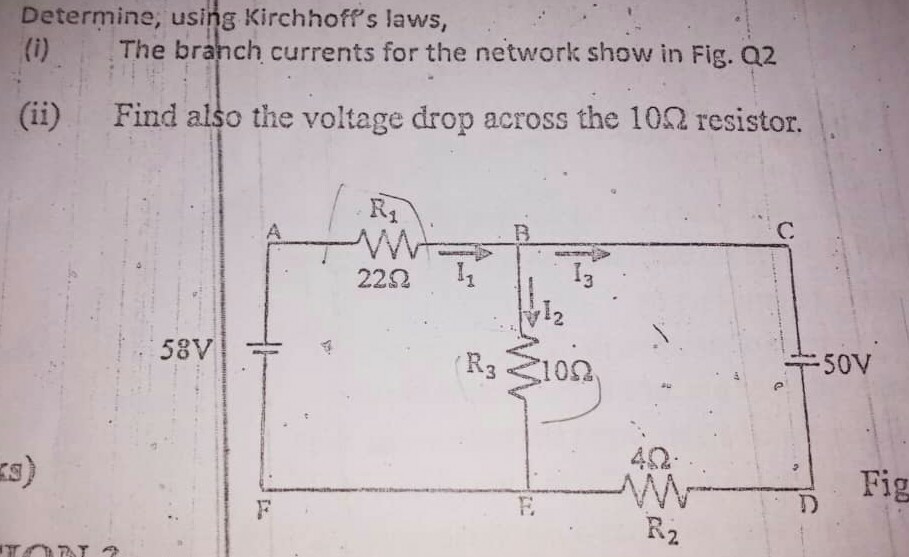
Question Number 82358 Answers: 0 Comments: 3
Question Number 82285 Answers: 0 Comments: 0

Question Number 82176 Answers: 0 Comments: 3

Question Number 82138 Answers: 0 Comments: 1

Question Number 82110 Answers: 0 Comments: 0

Question Number 82084 Answers: 0 Comments: 2
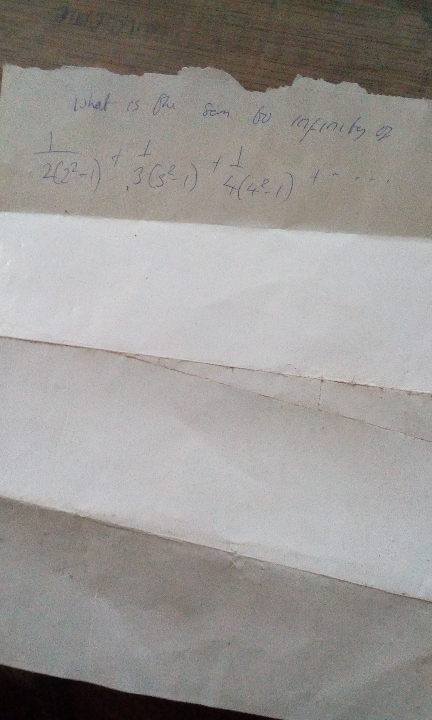
Question Number 82034 Answers: 0 Comments: 1
Question Number 81971 Answers: 1 Comments: 0
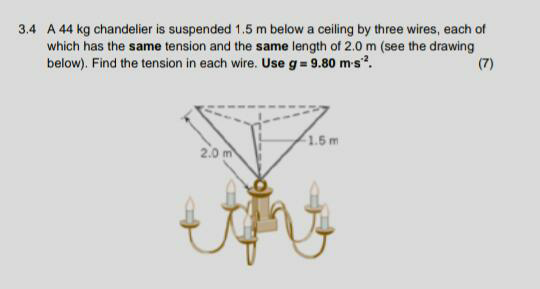
Question Number 81843 Answers: 2 Comments: 5

Question Number 81851 Answers: 0 Comments: 0
Question Number 81797 Answers: 0 Comments: 1

Question Number 81704 Answers: 0 Comments: 0
