Question and Answers Forum

OthersQuestion and Answers: Page 71

Question Number 90018 Answers: 1 Comments: 2

expand , ln(1 + sin x) right up to the term in x^3

$$\mathrm{expand}\:,\:\mathrm{ln}\left(\mathrm{1}\:+\:\mathrm{sin}\:{x}\right)\:\mathrm{right}\:\mathrm{up}\:\mathrm{to}\:\mathrm{the}\:\mathrm{term}\:\mathrm{in}\:{x}^{\mathrm{3}} \\ $$

Question Number 89986 Answers: 0 Comments: 3

∫_0 ^1 (−1)^(⌊(1/x)⌋) dx

$$\int_{\mathrm{0}} ^{\mathrm{1}} \left(−\mathrm{1}\right)^{\lfloor\frac{\mathrm{1}}{{x}}\rfloor} \:{dx} \\ $$

Question Number 89980 Answers: 0 Comments: 2

Question Number 89953 Answers: 0 Comments: 1

solvethefollowingequation 5^(2x+y) =625and2^(4x∤2y) =(1/6)

$$\mathrm{solvethefollowingequation} \\ $$$$\mathrm{5}^{\mathrm{2x}+\mathrm{y}} =\mathrm{625and2}^{\mathrm{4x}\nmid\mathrm{2y}} =\frac{\mathrm{1}}{\mathrm{6}} \\ $$

Question Number 89956 Answers: 0 Comments: 1

simplifyκgivingκyourκanswerκinκindexκform (√((ac^2 )/(9a^2 c^4 )))

$$\mathrm{simplify}\kappa\mathrm{giving}\kappa\mathrm{your}\kappa\mathrm{answer}\kappa\mathrm{in}\kappa\mathrm{index}\kappa\mathrm{form} \\ $$$$\sqrt{\frac{\mathrm{ac}^{\mathrm{2}} }{\mathrm{9a}^{\mathrm{2}} \mathrm{c}^{\mathrm{4}} }} \\ $$

Question Number 89937 Answers: 0 Comments: 1

Prove that for all complex such as ∣z∣<1= Σ_(n=1) ^∞ (z^n /((z^n −1)^2 )) +Σ_(n=1) ^∞ ((nz^n )/(z^n −1)) = 0

$${Prove}\:{that}\:{for}\:{all}\:{complex}\:{such}\:{as}\:\mid{z}\mid<\mathrm{1}= \\ $$$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{z}^{{n}} }{\left({z}^{{n}} −\mathrm{1}\right)^{\mathrm{2}} }\:+\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\:\frac{{nz}^{{n}} }{{z}^{{n}} −\mathrm{1}}\:=\:\mathrm{0}\: \\ $$

Question Number 89936 Answers: 1 Comments: 0

Prove that Σ_(p≥1,q≥1) (1/(pq(p+q−1))) =(π^2 /3)

$${Prove}\:{that}\:\underset{{p}\geqslant\mathrm{1},{q}\geqslant\mathrm{1}} {\sum}\:\:\frac{\mathrm{1}}{{pq}\left({p}+{q}−\mathrm{1}\right)}\:=\frac{\pi^{\mathrm{2}} }{\mathrm{3}}\: \\ $$

Question Number 89934 Answers: 0 Comments: 0

Let x∈]0;1[ Prove that Σ_(n=1) ^∞ (x^n /(1+x^n )) +Σ_(n=1) ^∞ (((−x)^n )/(1−x^n )) = 0

$$\left.{Let}\:{x}\in\right]\mathrm{0};\mathrm{1}\left[\:\:{Prove}\:{that}\right. \\ $$$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{x}^{{n}} }{\mathrm{1}+{x}^{{n}} }\:+\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−{x}\right)^{{n}} }{\mathrm{1}−{x}^{{n}} }\:=\:\mathrm{0} \\ $$

Question Number 89745 Answers: 0 Comments: 2

f(x) = f(x+((3π)/8)) , ∀x∈ R if ∫_0 ^(3π/8) f(x) dx = t , then ∫_π ^(5π/2) f(x−π) dx = A. 2t B. 3t C. 4t D. 6t E. 8t

$$\mathrm{f}\left(\mathrm{x}\right)\:=\:\mathrm{f}\left(\mathrm{x}+\frac{\mathrm{3}\pi}{\mathrm{8}}\right)\:,\:\forall\mathrm{x}\in\:\mathbb{R} \\ $$$$\mathrm{if}\:\underset{\mathrm{0}} {\overset{\mathrm{3}\pi/\mathrm{8}} {\int}}\mathrm{f}\left(\mathrm{x}\right)\:\mathrm{dx}\:=\:\mathrm{t}\:,\:\mathrm{then}\: \\ $$$$\underset{\pi} {\overset{\mathrm{5}\pi/\mathrm{2}} {\int}}\mathrm{f}\left(\mathrm{x}−\pi\right)\:\mathrm{dx}\:=\: \\ $$$$\mathrm{A}.\:\mathrm{2t}\:\:\:\:\:\:\:\mathrm{B}.\:\mathrm{3t}\:\:\:\:\:\:\:\mathrm{C}.\:\mathrm{4t}\:\:\:\:\:\:\:\mathrm{D}.\:\mathrm{6t} \\ $$$$\mathrm{E}.\:\mathrm{8t}\: \\ $$

Question Number 89728 Answers: 1 Comments: 0

Find the area bounded by 3x+4y=12 and the coordinate axes?

$${Find}\:{the}\:{area}\:{bounded}\:{by}\:\mathrm{3}{x}+\mathrm{4}{y}=\mathrm{12} \\ $$$${and}\:{the}\:{coordinate}\:{axes}? \\ $$

Question Number 89661 Answers: 0 Comments: 3

The Area of the triangle is 9x^2 −12x+4. compute its perimeter?

$${The}\:{Area}\:{of}\:{the}\:{triangle}\:{is}\:\mathrm{9}{x}^{\mathrm{2}} \:−\mathrm{12}{x}+\mathrm{4}. \\ $$$${compute}\:{its}\:{perimeter}? \\ $$

Question Number 89626 Answers: 0 Comments: 1

Question Number 89620 Answers: 0 Comments: 0

x=^(c−1) (√((ay−bz)/(cdy))) What will happen to x when a increses? Explain.

$${x}=^{{c}−\mathrm{1}} \sqrt{\frac{{ay}−{bz}}{{cdy}}} \\ $$$$ \\ $$$$\mathrm{What}\:\mathrm{will}\:\mathrm{happen}\:\mathrm{to}\:\boldsymbol{{x}}\:\mathrm{when}\:\boldsymbol{{a}}\:\mathrm{increses}? \\ $$$$\mathrm{Explain}. \\ $$

Question Number 89446 Answers: 0 Comments: 1

$$.. \\ $$

Question Number 89324 Answers: 0 Comments: 1

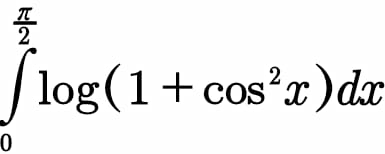
Question Number 89244 Answers: 0 Comments: 1

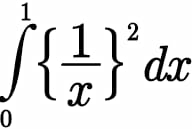
Question Number 89236 Answers: 1 Comments: 0

z(z^2 +3x)+3y=0 show that (∂^2 z/∂x^2 )+(∂^2 z/∂y^2 )=((2z(x−1))/((z^2 +x)^3 ))

$$\mathrm{z}\left(\mathrm{z}^{\mathrm{2}} +\mathrm{3x}\right)+\mathrm{3y}=\mathrm{0} \\ $$$$\mathrm{show}\:\mathrm{that} \\ $$$$\frac{\partial^{\mathrm{2}} \mathrm{z}}{\partial\mathrm{x}^{\mathrm{2}} }+\frac{\partial^{\mathrm{2}} \mathrm{z}}{\partial\mathrm{y}^{\mathrm{2}} }=\frac{\mathrm{2z}\left(\mathrm{x}−\mathrm{1}\right)}{\left(\mathrm{z}^{\mathrm{2}} +\mathrm{x}\right)^{\mathrm{3}} } \\ $$

Question Number 89238 Answers: 1 Comments: 1

∫_7 ^(12) x^2 (√(x−3))

$$\int_{\mathrm{7}} ^{\mathrm{12}} \mathrm{x}^{\mathrm{2}} \sqrt{\mathrm{x}−\mathrm{3}} \\ $$

Question Number 89200 Answers: 0 Comments: 0

Question Number 89144 Answers: 0 Comments: 0

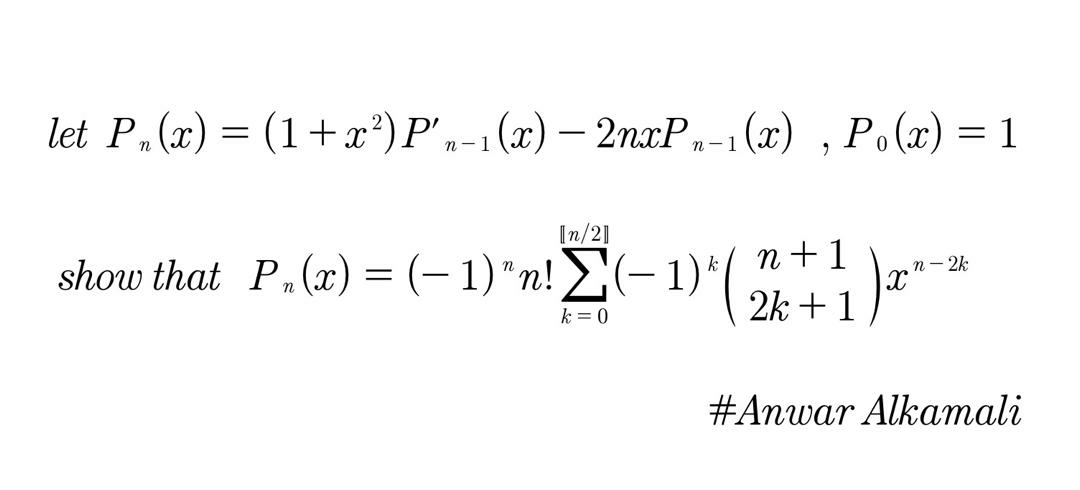
Question Number 89143 Answers: 0 Comments: 0

Question Number 89126 Answers: 0 Comments: 0

6[(√( ))

$$\mathrm{6}\left[\sqrt{\:\:}\right. \\ $$

Question Number 89093 Answers: 0 Comments: 0

Question Number 89092 Answers: 0 Comments: 2

Evaluate : lim_(n→∞) e^(−n) Σ_(k=0) ^n (n^k /(k!))

$${Evaluate}\::\:\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:{e}^{−{n}} \:\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\frac{{n}^{{k}} }{{k}!} \\ $$

Question Number 89074 Answers: 0 Comments: 1

×^4 +×^2 =1

$$×^{\mathrm{4}} +×^{\mathrm{2}} =\mathrm{1} \\ $$

Question Number 89063 Answers: 0 Comments: 0

let f(x) = x^3 + 2x^2 + 3x + 4 find the region enclosed by f ′, f ′′ and f ′′′

$$\:\mathrm{let}\:{f}\left({x}\right)\:=\:{x}^{\mathrm{3}} \:+\:\mathrm{2}{x}^{\mathrm{2}} \:+\:\mathrm{3}{x}\:+\:\mathrm{4} \\ $$$$\:\mathrm{find}\:\mathrm{the}\:\mathrm{region}\:\mathrm{enclosed}\:\mathrm{by}\:{f}\:',\:{f}\:''\:\mathrm{and}\:{f}\:''' \\ $$

Pg 66 Pg 67 Pg 68 Pg 69 Pg 70 Pg 71 Pg 72 Pg 73 Pg 74 Pg 75

Contact: info@tinkutara.com