
OthersQuestion and Answers: Page 70
Question Number 91638 Answers: 1 Comments: 0
Question Number 91613 Answers: 1 Comments: 4
Question Number 91604 Answers: 0 Comments: 0

Question Number 91588 Answers: 0 Comments: 2
$${what}\:{is}\:{f}^{−\mathrm{1}} \:{for}\:{f}\left({x}\right)=\lfloor{x}\rfloor?? \\ $$
Question Number 91476 Answers: 0 Comments: 2
Question Number 91421 Answers: 2 Comments: 2
Question Number 91375 Answers: 0 Comments: 3
Question Number 91374 Answers: 0 Comments: 0
Question Number 91303 Answers: 0 Comments: 3
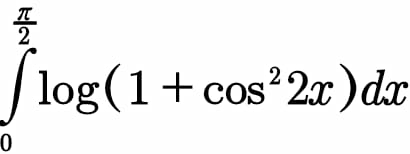
Question Number 91302 Answers: 2 Comments: 0

Question Number 91297 Answers: 0 Comments: 2
Question Number 91149 Answers: 1 Comments: 1
Question Number 91119 Answers: 0 Comments: 0
Question Number 91099 Answers: 1 Comments: 12
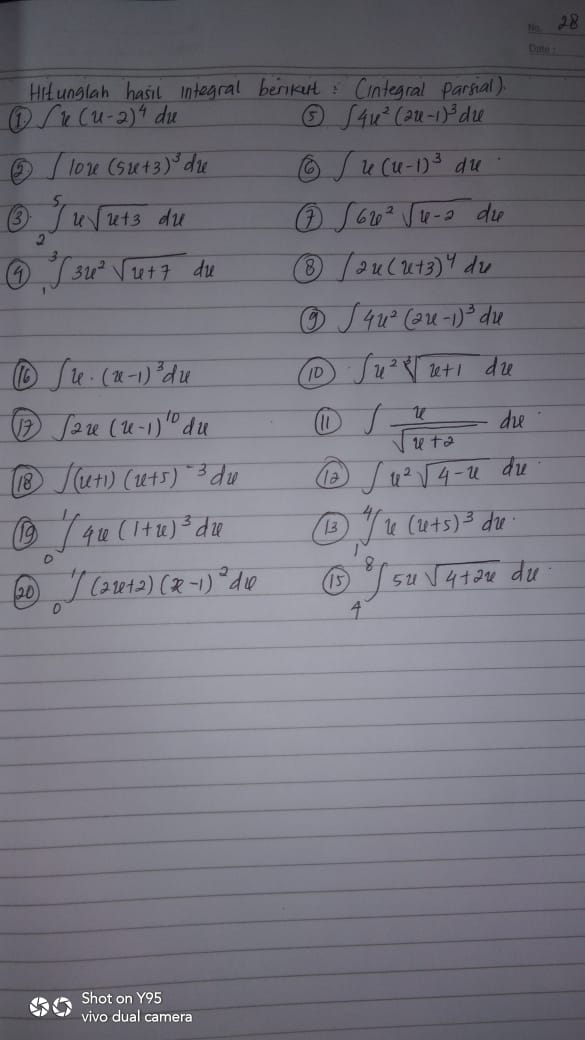
Question Number 90947 Answers: 0 Comments: 0
Question Number 90940 Answers: 1 Comments: 0
Question Number 90709 Answers: 0 Comments: 2
Question Number 90692 Answers: 1 Comments: 2

Question Number 92777 Answers: 1 Comments: 2
Question Number 90647 Answers: 0 Comments: 14

Question Number 90581 Answers: 1 Comments: 0
Question Number 90316 Answers: 1 Comments: 2
Question Number 90138 Answers: 0 Comments: 2
$$\int{x}\sqrt{\mathrm{3}{x}^{\mathrm{3}} +\mathrm{7}}\:{dx} \\ $$
Question Number 90099 Answers: 0 Comments: 2
Question Number 90046 Answers: 0 Comments: 0
Question Number 90024 Answers: 0 Comments: 2
