Question and Answers Forum

All Questions Topic List

OthersQuestion and Answers: Page 69

Question Number 92910 Answers: 2 Comments: 2

∫(dt/(3sint+4cost))

$$\int\frac{\mathrm{dt}}{\mathrm{3sint}+\mathrm{4cost}} \\ $$

Question Number 92888 Answers: 1 Comments: 3

∫((5−t)/(1+(√((t−4)))))dt

$$\int\frac{\mathrm{5}−\mathrm{t}}{\mathrm{1}+\sqrt{\left(\mathrm{t}−\mathrm{4}\right)}}\mathrm{dt} \\ $$$$ \\ $$

Question Number 92898 Answers: 0 Comments: 0

Find a,b,c ∈ Z that satisfy (7a + 15b + 0c) mod 26 = 8 (5a + 16b + 6c) mod 26 = 21 (6a + 3b + 20c) mod 26 = 14

$$\mathrm{Find}\:{a},{b},{c}\:\in\:\mathbb{Z}\:\mathrm{that}\:\mathrm{satisfy} \\ $$$$\left(\mathrm{7}{a}\:+\:\mathrm{15}{b}\:+\:\mathrm{0}{c}\right)\:\mathrm{mod}\:\mathrm{26}\:=\:\mathrm{8} \\ $$$$\left(\mathrm{5}{a}\:+\:\mathrm{16}{b}\:+\:\mathrm{6}{c}\right)\:\mathrm{mod}\:\mathrm{26}\:=\:\mathrm{21} \\ $$$$\left(\mathrm{6}{a}\:+\:\mathrm{3}{b}\:+\:\mathrm{20}{c}\right)\:\mathrm{mod}\:\mathrm{26}\:=\:\mathrm{14} \\ $$

Question Number 92788 Answers: 0 Comments: 0

Question Number 92708 Answers: 1 Comments: 0

solve the differential equations. (a) (x + 3y^2 )(d^2 y/dx^2 ) + 6y ((dy/dx))^2 + 2(dy/dx) + 2 = 0 (b) (2y−x)(d^2 y/dx^2 ) + 2((dy/dx))^2 −2 (dy/dx) + 2 = 0

$$\mathrm{solve}\:\mathrm{the}\:\mathrm{differential}\:\mathrm{equations}. \\ $$$$\:\left(\mathrm{a}\right)\:\left({x}\:+\:\mathrm{3}{y}^{\mathrm{2}} \right)\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }\:+\:\mathrm{6}{y}\:\left(\frac{{dy}}{{dx}}\right)^{\mathrm{2}} \:+\:\mathrm{2}\frac{{dy}}{{dx}}\:+\:\mathrm{2}\:=\:\mathrm{0} \\ $$$$\left(\mathrm{b}\right)\:\left(\mathrm{2}{y}−{x}\right)\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }\:+\:\mathrm{2}\left(\frac{{dy}}{{dx}}\right)^{\mathrm{2}} \:−\mathrm{2}\:\frac{{dy}}{{dx}}\:+\:\mathrm{2}\:=\:\mathrm{0} \\ $$

Question Number 92712 Answers: 0 Comments: 2

find m for fix function f(x)=(((m−1)x+3)/(x−1))

$${find}\:\:\boldsymbol{{m}}\:{for}\:{fix}\:{function} \\ $$$${f}\left({x}\right)=\frac{\left(\boldsymbol{{m}}−\mathrm{1}\right){x}+\mathrm{3}}{{x}−\mathrm{1}} \\ $$

Question Number 92605 Answers: 1 Comments: 4

If ((1+x)/(1+(√(1+x)))) +((1−x)/(1−(√(1−x)))) =1 find x

$${If}\:\frac{\mathrm{1}+{x}}{\mathrm{1}+\sqrt{\mathrm{1}+{x}}}\:+\frac{\mathrm{1}−{x}}{\mathrm{1}−\sqrt{\mathrm{1}−{x}}}\:=\mathrm{1} \\ $$$${find}\:{x} \\ $$

Question Number 92593 Answers: 0 Comments: 0

using the squeeze theorem show that lim_(x→a) (√x) = (√a)

$$\mathrm{using}\:\mathrm{the}\:\mathrm{squeeze}\:\mathrm{theorem}\: \\ $$$$\mathrm{show}\:\mathrm{that} \\ $$$$\:\:\underset{{x}\rightarrow{a}} {\mathrm{lim}}\:\sqrt{{x}}\:=\:\sqrt{{a}}\: \\ $$

Question Number 92555 Answers: 0 Comments: 5

Σ_(n=1) ^∞ 1/n^2 =π^2 /6

$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\mathrm{1}/{n}^{\mathrm{2}} =\pi^{\mathrm{2}} /\mathrm{6} \\ $$

Question Number 92529 Answers: 0 Comments: 0

two smooth spheres of masses 2m and 3m have velocites (−12i + 8j) u ms^(−1) and (5i + 12j)u , respectively where u is a constant. The spheres collide with thier line of centre of parallel to j. Given that the coefficient of restitution between the spheres is (1/4), find the loss in kinetic energy due to impact.

$$\mathrm{two}\:\mathrm{smooth}\:\mathrm{spheres}\:\mathrm{of}\:\mathrm{masses}\:\mathrm{2}{m}\:\mathrm{and}\:\mathrm{3}{m}\:\mathrm{have}\:\mathrm{velocites} \\ $$$$\left(−\mathrm{12}\boldsymbol{\mathrm{i}}\:+\:\mathrm{8}\boldsymbol{\mathrm{j}}\right)\:{u}\:\mathrm{ms}^{−\mathrm{1}} \:\mathrm{and}\:\left(\mathrm{5}\boldsymbol{\mathrm{i}}\:+\:\mathrm{12}\boldsymbol{\mathrm{j}}\right){u}\:,\:\mathrm{respectively}\:\mathrm{where}\:{u}\: \\ $$$$\mathrm{is}\:\mathrm{a}\:\mathrm{constant}.\:\mathrm{The}\:\mathrm{spheres}\:\mathrm{collide}\:\mathrm{with}\:\mathrm{thier}\:\mathrm{line}\:\mathrm{of}\:\mathrm{centre}\:\mathrm{of} \\ $$$$\mathrm{parallel}\:\mathrm{to}\:\boldsymbol{\mathrm{j}}.\:\mathrm{Given}\:\mathrm{that}\:\mathrm{the}\:\mathrm{coefficient}\:\mathrm{of}\:\mathrm{restitution}\:\mathrm{between} \\ $$$$\mathrm{the}\:\mathrm{spheres}\:\mathrm{is}\:\frac{\mathrm{1}}{\mathrm{4}},\:\mathrm{find}\:\mathrm{the}\:\mathrm{loss}\:\mathrm{in}\:\mathrm{kinetic}\:\mathrm{energy}\:\mathrm{due}\:\mathrm{to}\:\mathrm{impact}. \\ $$

Question Number 92474 Answers: 0 Comments: 0

please anyone wanna help me with Q91948

$$\mathrm{please}\:\mathrm{anyone}\:\mathrm{wanna}\:\mathrm{help}\:\mathrm{me}\:\mathrm{with}\:\mathrm{Q91948} \\ $$

Question Number 92465 Answers: 1 Comments: 7

for a 2d vectors if ∣a + b∣ = ∣a−b∣ what relationship does a and b have?

$$\mathrm{for}\:\mathrm{a}\:\mathrm{2d}\:\:\mathrm{vectors}\:\mathrm{if}\:\mid{a}\:+\:{b}\mid\:=\:\mid{a}−{b}\mid\:\mathrm{what}\:\mathrm{relationship}\:\mathrm{does}\:{a}\:\mathrm{and}\:{b}\:\mathrm{have}? \\ $$$$ \\ $$

Question Number 92344 Answers: 0 Comments: 3

∫_0 ^1 (dx/((√(1+3x))−(√(1−3x))))

$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{dx}}{\sqrt{\mathrm{1}+\mathrm{3x}}−\sqrt{\mathrm{1}−\mathrm{3x}}} \\ $$

Question Number 92055 Answers: 0 Comments: 3

∫(((x+1)/((x^2 +4x+5)^2 )))dx

$$\int\left(\frac{\mathrm{x}+\mathrm{1}}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{4x}+\mathrm{5}\right)^{\mathrm{2}} }\right)\mathrm{dx} \\ $$

Question Number 92010 Answers: 1 Comments: 0

if log_6 30 = a and log_(24) 15 = b log_(12) 60 = ?

$$\mathrm{if}\:\mathrm{log}_{\mathrm{6}} \mathrm{30}\:=\:{a}\:\mathrm{and}\:\mathrm{log}_{\mathrm{24}} \mathrm{15}\:=\:{b} \\ $$$$\mathrm{log}_{\mathrm{12}} \mathrm{60}\:=\:? \\ $$

Question Number 91995 Answers: 0 Comments: 1

hello what is the metric of schwarzchild dynamics.

$${hello}\:{what}\:{is}\:{the}\:{metric}\:{of}\:{schwarzchild}\:{dynamics}. \\ $$

Question Number 92025 Answers: 2 Comments: 1

∫(((x−1)/(x^2 −x−1)))dx

$$\int\left(\frac{\mathrm{x}−\mathrm{1}}{\mathrm{x}^{\mathrm{2}} −\mathrm{x}−\mathrm{1}}\right)\mathrm{dx} \\ $$

Question Number 91948 Answers: 0 Comments: 1

Question Number 91946 Answers: 2 Comments: 3

a particle is projected from a point at a height 3h metres above a horizontal play ground. the direction of the projectile makes an angle α with the horizontal through the point of projection. show that if th greatest height reached above the point lc projection is h metres, then the horizontal distance travelled by the particle before striking the plane is 6h cotα metres. Find the vertical and horizontal component of the speed of the particle just before it hits the ground.

Question Number 91931 Answers: 0 Comments: 3

∫_0 ^1 ln(Γ(x)) dx

$$\int_{\mathrm{0}} ^{\mathrm{1}} {ln}\left(\Gamma\left({x}\right)\right)\:{dx} \\ $$

Question Number 91930 Answers: 0 Comments: 2

lim_(x→0) cos (1/x)=

$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}cos}\:\frac{\mathrm{1}}{{x}}= \\ $$

Question Number 91785 Answers: 0 Comments: 5

given these bellow sequenses . find fifth term 1). (1/5), (1/4) , (3/(11)), (2/7),... 2). (3/5), ((−9)/(11)) , ((−25)/(19)), ((57)/(35)),... 3). (1/6), (7/(11)) , ((13)/(16)), ((19)/(21)),... 4). 4,− (2/3) , −(4/(13)),− (1/5),... 5). 2, 9 , 28 , 65,...

$$\mathrm{given}\:\:\mathrm{these}\:\mathrm{bellow}\:\mathrm{sequenses}\:.\: \\ $$$$\mathrm{find}\:\mathrm{fifth}\:\mathrm{term} \\ $$$$ \\ $$$$\left.\mathrm{1}\right).\:\:\frac{\mathrm{1}}{\mathrm{5}},\:\frac{\mathrm{1}}{\mathrm{4}}\:,\:\frac{\mathrm{3}}{\mathrm{11}},\:\frac{\mathrm{2}}{\mathrm{7}},... \\ $$$$\left.\mathrm{2}\right).\:\:\frac{\mathrm{3}}{\mathrm{5}},\:\frac{−\mathrm{9}}{\mathrm{11}}\:,\:\frac{−\mathrm{25}}{\mathrm{19}},\:\frac{\mathrm{57}}{\mathrm{35}},... \\ $$$$\left.\mathrm{3}\right).\:\:\:\frac{\mathrm{1}}{\mathrm{6}},\:\frac{\mathrm{7}}{\mathrm{11}}\:,\:\frac{\mathrm{13}}{\mathrm{16}},\:\frac{\mathrm{19}}{\mathrm{21}},... \\ $$$$\left.\mathrm{4}\right).\:\:\:\mathrm{4},−\:\frac{\mathrm{2}}{\mathrm{3}}\:,\:−\frac{\mathrm{4}}{\mathrm{13}},−\:\frac{\mathrm{1}}{\mathrm{5}},... \\ $$$$\left.\mathrm{5}\right).\:\:\mathrm{2},\:\mathrm{9}\:,\:\mathrm{28}\:,\:\mathrm{65},... \\ $$

Question Number 91783 Answers: 0 Comments: 1

1). (1/2), (2/3), (3/4) , (4/5), ..., .... 2). 4,6,10,18,34,...,.... 3). 5,7,11,19,35,...,.... 4). 4,6,10,18,34,...,.... 5). 4,11,30,85,248,...,...

$$\left.\mathrm{1}\right).\:\:\frac{\mathrm{1}}{\mathrm{2}},\:\frac{\mathrm{2}}{\mathrm{3}},\:\frac{\mathrm{3}}{\mathrm{4}}\:,\:\frac{\mathrm{4}}{\mathrm{5}},\:...,\:.... \\ $$$$\left.\mathrm{2}\right).\:\:\mathrm{4},\mathrm{6},\mathrm{10},\mathrm{18},\mathrm{34},...,.... \\ $$$$\left.\mathrm{3}\right).\:\:\mathrm{5},\mathrm{7},\mathrm{11},\mathrm{19},\mathrm{35},...,.... \\ $$$$\left.\mathrm{4}\right).\:\:\mathrm{4},\mathrm{6},\mathrm{10},\mathrm{18},\mathrm{34},...,.... \\ $$$$\left.\mathrm{5}\right).\:\:\mathrm{4},\mathrm{11},\mathrm{30},\mathrm{85},\mathrm{248},...,... \\ $$

Question Number 91715 Answers: 0 Comments: 4

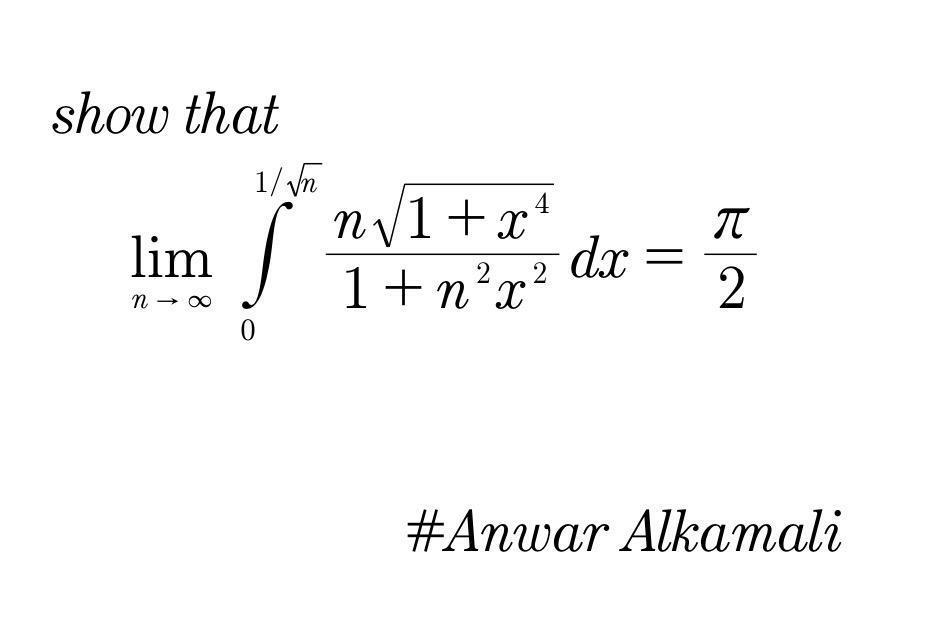
Question Number 91655 Answers: 2 Comments: 12

A particle is projected with an intial velocity of u ms^(−1) at an angle α to the ground from a point O on the ground. Given that it clears two walls of hieght h and distances 2h and 4h respectively from O. (a) find the tangent of α (b) the maximum hieght (c) the range and period of the particle (d) show that u^2 = (4/(26)) gh please sir can you help me using the actual equations of projectile motion?

$$\mathrm{A}\:\mathrm{particle}\:\mathrm{is}\:\mathrm{projected}\:\mathrm{with}\:\mathrm{an}\:\mathrm{intial}\:\mathrm{velocity}\:\mathrm{of}\:{u}\:\mathrm{ms}^{−\mathrm{1}} \:\mathrm{at}\:\mathrm{an}\:\mathrm{angle}\:\alpha\:\mathrm{to}\: \\ $$$$\mathrm{the}\:\mathrm{ground}\:\mathrm{from}\:\mathrm{a}\:\mathrm{point}\:\mathrm{O}\:\mathrm{on}\:\mathrm{the}\:\mathrm{ground}.\:\mathrm{Given}\:\mathrm{that}\:\mathrm{it}\:\mathrm{clears} \\ $$$$\mathrm{two}\:\mathrm{walls}\:\mathrm{of}\:\mathrm{hieght}\:{h}\:\mathrm{and}\:\mathrm{distances}\:\mathrm{2h}\:\mathrm{and}\:\mathrm{4h}\:\mathrm{respectively}\:\mathrm{from}\:\mathrm{O}. \\ $$$$\left(\mathrm{a}\right)\:\mathrm{find}\:\mathrm{the}\:\mathrm{tangent}\:\mathrm{of}\:\alpha \\ $$$$\left(\mathrm{b}\right)\:\mathrm{the}\:\mathrm{maximum}\:\mathrm{hieght} \\ $$$$\left(\mathrm{c}\right)\:\mathrm{the}\:\mathrm{range}\:\mathrm{and}\:\mathrm{period}\:\mathrm{of}\:\mathrm{the}\:\mathrm{particle} \\ $$$$\left(\mathrm{d}\right)\:\mathrm{show}\:\mathrm{that}\:{u}^{\mathrm{2}} \:=\:\frac{\mathrm{4}}{\mathrm{26}}\:\mathrm{g}{h}\: \\ $$$$\mathrm{please}\:\mathrm{sir}\:\mathrm{can}\:\mathrm{you}\:\mathrm{help}\:\mathrm{me}\:\mathrm{using}\:\mathrm{the}\:\mathrm{actual}\:\mathrm{equations}\:\mathrm{of}\:\mathrm{projectile}\:\mathrm{motion}? \\ $$$$ \\ $$

Question Number 91654 Answers: 1 Comments: 0

th position vector of a particle p of mass 3 kg is given by r = [(cos 2t) i + (sin 2t)j] m given that p was intitialy at rest. find the cartesian equation of its path and describe it.

$$\mathrm{th}\:\mathrm{position}\:\mathrm{vector}\:\mathrm{of}\:\mathrm{a}\:\mathrm{particle}\:{p}\:\mathrm{of}\:\mathrm{mass}\:\mathrm{3}\:\mathrm{kg}\:\mathrm{is}\:\mathrm{given}\:\mathrm{by}\: \\ $$$$\:{r}\:=\:\left[\left(\mathrm{cos}\:\mathrm{2}{t}\right)\:{i}\:+\:\left(\mathrm{sin}\:\mathrm{2}{t}\right){j}\right]\:\mathrm{m} \\ $$$$\mathrm{given}\:\mathrm{that}\:{p}\:\:\mathrm{was}\:\mathrm{intitialy}\:\mathrm{at}\:\mathrm{rest}. \\ $$$$\mathrm{find}\:\mathrm{the}\:\mathrm{cartesian}\:\mathrm{equation}\:\mathrm{of}\:\mathrm{its}\:\mathrm{path}\:\mathrm{and}\:\mathrm{describe}\:\mathrm{it}. \\ $$

Pg 64 Pg 65 Pg 66 Pg 67 Pg 68 Pg 69 Pg 70 Pg 71 Pg 72 Pg 73

Contact: info@tinkutara.com