Question and Answers Forum

OthersQuestion and Answers: Page 67

Question Number 96667 Answers: 2 Comments: 0

Prove that Σ_(k=1) ^∞ (1/k^2 )=(π^2 /6)

$$\mathcal{P}\mathrm{rove}\:\:\mathrm{that}\:\:\underset{\mathrm{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\mathrm{k}^{\mathrm{2}} }=\frac{\pi^{\mathrm{2}} }{\mathrm{6}} \\ $$

Question Number 96358 Answers: 0 Comments: 0

Question Number 96290 Answers: 0 Comments: 1

If : tan(x +iy) = a + bi then find a,b

$${If}\::\:\mathrm{tan}\left({x}\:+{iy}\right)\:=\:{a}\:+\:{bi}\: \\ $$$${then}\:{find}\:{a},{b} \\ $$

Question Number 96108 Answers: 0 Comments: 0

are the system (z,+,≤)is orderd integral domain ?

$${are}\:{the}\:{system}\:\left({z},+,\leqslant\right){is}\:{orderd}\:{integral}\:{domain}\:? \\ $$

Question Number 96052 Answers: 1 Comments: 0

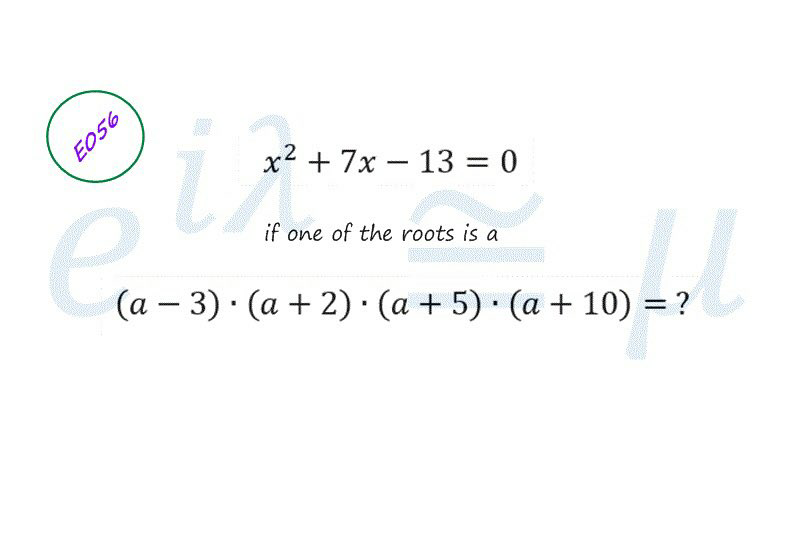
Question Number 96041 Answers: 1 Comments: 0

if f(x)=3^x^(2+x^3 ) find f′(x)?

$${if}\:{f}\left({x}\right)=\mathrm{3}^{{x}^{\mathrm{2}+{x}^{\mathrm{3}} } } \:\:\:{find}\:{f}'\left({x}\right)? \\ $$

Question Number 96008 Answers: 0 Comments: 1

((1−(1/a))/(a^2 −(1/a^2 )))

$$\frac{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{a}}}{\mathrm{a}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{a}^{\mathrm{2}} }} \\ $$

Question Number 96007 Answers: 0 Comments: 1

((9x^2 +4a^2 )/(9x^2 −4a^2 )) +((3x)/(3x+2a)) −((2a)/(2a−3x))

$$\frac{\mathrm{9x}^{\mathrm{2}} +\mathrm{4a}^{\mathrm{2}} }{\mathrm{9x}^{\mathrm{2}} −\mathrm{4a}^{\mathrm{2}} }\:+\frac{\mathrm{3x}}{\mathrm{3x}+\mathrm{2a}}\:−\frac{\mathrm{2a}}{\mathrm{2a}−\mathrm{3x}} \\ $$

Question Number 96026 Answers: 0 Comments: 1

sin (p/x)=1

$$\mathrm{sin}\:\frac{\mathrm{p}}{\mathrm{x}}=\mathrm{1} \\ $$

Question Number 95670 Answers: 0 Comments: 0

Question Number 95604 Answers: 1 Comments: 3

Question Number 95473 Answers: 1 Comments: 0

Question Number 95420 Answers: 0 Comments: 7

tinkutara admint I want to update to version 2.074

$$\mathrm{tinkutara}\:\mathrm{admint} \\ $$$$\mathrm{I}\:\mathrm{want}\:\mathrm{to}\:\mathrm{update}\:\mathrm{to}\:\mathrm{version}\:\mathrm{2}.\mathrm{074} \\ $$

Question Number 95259 Answers: 1 Comments: 1

find all roots ((√6) −(√2)i)^(1/3) by using demover theorem ?

$${find}\:{all}\:{roots}\:\left(\sqrt{\mathrm{6}}\:−\sqrt{\mathrm{2}}{i}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} {by}\:{using}\:{demover}\:{theorem}\:? \\ $$

Question Number 95121 Answers: 1 Comments: 1

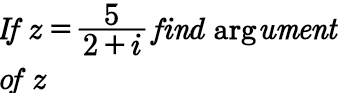
Question Number 95020 Answers: 1 Comments: 1

Question Number 94914 Answers: 1 Comments: 0

Question Number 94820 Answers: 1 Comments: 0

A train which travels at a uniform speed due to mechanical fault after traveling for an hour goes at 3/5 th of the original speed and reaches the destination 2 hours late. If the fault occured after traveling another 50 miles the train would have reached 40 minutes earlier. What is the distance between the two stations ?

$${A}\:{train}\:{which}\:{travels}\:{at}\:{a}\:{uniform}\:{speed}\:{due}\:{to}\:{mechanical}\:{fault}\:{after}\: \\ $$$${traveling}\:{for}\:{an}\:{hour}\:{goes}\:{at}\:\mathrm{3}/\mathrm{5}\:{th}\:{of}\:{the}\:{original}\:{speed}\:{and}\:{reaches}\:{the}\: \\ $$$${destination}\:\mathrm{2}\:{hours}\:{late}.\:{If}\:{the}\:{fault}\:{occured}\:{after}\:{traveling}\:{another}\:\mathrm{50} \\ $$$${miles}\:{the}\:{train}\:{would}\:{have}\:{reached}\:\mathrm{40}\:{minutes}\:{earlier}.\:{What}\:{is}\:{the}\: \\ $$$${distance}\:{between}\:{the}\:{two}\:{stations}\:? \\ $$

Question Number 94782 Answers: 1 Comments: 0

The velocity of physical quantities is given by v = (√((P + (1/n))/x)) , where P is the pressure. Find the dimention of n and x.

$$\mathrm{The}\:\mathrm{velocity}\:\mathrm{of}\:\mathrm{physical}\:\mathrm{quantities}\:\mathrm{is}\:\mathrm{given}\:\mathrm{by} \\ $$$$\:\:\mathrm{v}\:\:=\:\:\sqrt{\frac{\mathrm{P}\:\:+\:\:\frac{\mathrm{1}}{\mathrm{n}}}{\mathrm{x}}}\:,\:\:\mathrm{where}\:\:\mathrm{P}\:\mathrm{is}\:\mathrm{the}\:\mathrm{pressure}. \\ $$$$\mathrm{Find}\:\mathrm{the}\:\mathrm{dimention}\:\mathrm{of}\:\:\:\mathrm{n}\:\:\mathrm{and}\:\:\mathrm{x}. \\ $$

Question Number 94769 Answers: 2 Comments: 0

Question Number 94739 Answers: 2 Comments: 2

Question Number 94455 Answers: 1 Comments: 3

Solve (D^2 −2D+1)y=xe^x sinx pleas help me sir

$${Solve}\:\left({D}^{\mathrm{2}} −\mathrm{2}{D}+\mathrm{1}\right){y}={xe}^{{x}} {sinx}\: \\ $$$${pleas}\:{help}\:{me}\:{sir}\: \\ $$

Question Number 94419 Answers: 0 Comments: 0

Let G be a connected graph and let X be the set of vertices of G of odd degree. suppose that ∣X∣=2k, where k≥1 show that there are k edge-disjoint trail Q_1 , Q_2 ,...,Q_k in G such that E(G)=E(Q_1 )∪E(Q_2 )∪....∪E(Q_k )

$${Let}\:{G}\:{be}\:{a}\:{connected}\:{graph}\:{and}\:{let}\:{X}\:{be}\:{the}\:{set}\:{of}\:{vertices}\:{of}\:{G}\:{of}\:{odd}\:{degree}.\:{suppose}\:{that}\:\mid{X}\mid=\mathrm{2}{k},\:{where}\:{k}\geqslant\mathrm{1}\: \\ $$$${show}\:{that}\:{there}\:{are}\:{k}\:{edge}-{disjoint}\:{trail}\:{Q}_{\mathrm{1}} ,\:{Q}_{\mathrm{2}} ,...,{Q}_{{k}} \:{in}\:{G}\:{such}\:{that} \\ $$$${E}\left({G}\right)={E}\left({Q}_{\mathrm{1}} \right)\cup{E}\left({Q}_{\mathrm{2}} \right)\cup....\cup{E}\left({Q}_{{k}} \right) \\ $$

Question Number 94360 Answers: 1 Comments: 3

Question Number 94359 Answers: 0 Comments: 1

If 32 men can reap a field in 15 days .In howmany days can 20 men reap the same fied?

$${If}\:\:\mathrm{32}\:{men}\:{can}\:{reap}\:{a}\:{field}\:{in}\:\mathrm{15}\:{days}\:.{In}\:{howmany}\:{days}\:{can}\:\mathrm{20}\:{men}\:{reap}\:{the}\:{same}\:{fied}? \\ $$

Question Number 94319 Answers: 0 Comments: 4

Pg 62 Pg 63 Pg 64 Pg 65 Pg 66 Pg 67 Pg 68 Pg 69 Pg 70 Pg 71

Contact: info@tinkutara.com