
OthersQuestion and Answers: Page 66
Question Number 99097 Answers: 0 Comments: 1
Question Number 98953 Answers: 2 Comments: 0
Question Number 98924 Answers: 0 Comments: 0
Question Number 98887 Answers: 0 Comments: 0

Question Number 98673 Answers: 2 Comments: 0
Question Number 98640 Answers: 0 Comments: 1

Question Number 98638 Answers: 0 Comments: 2
Question Number 98620 Answers: 1 Comments: 0
Question Number 98468 Answers: 2 Comments: 10

Question Number 98443 Answers: 1 Comments: 0
Question Number 98320 Answers: 1 Comments: 0

Question Number 98208 Answers: 0 Comments: 2
Question Number 98290 Answers: 0 Comments: 1
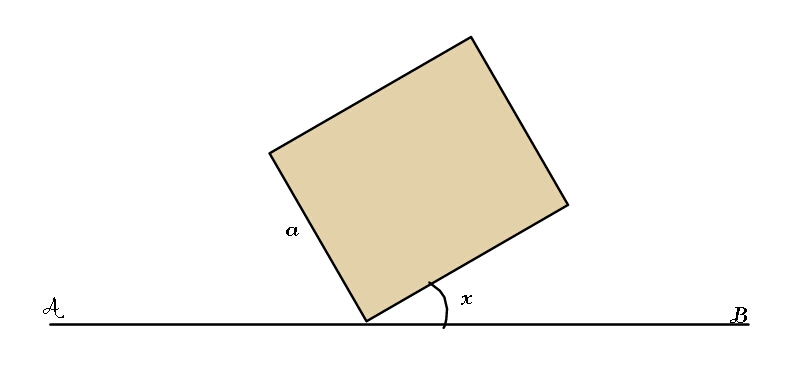
Question Number 98022 Answers: 1 Comments: 0
Question Number 97953 Answers: 1 Comments: 3

Question Number 97833 Answers: 0 Comments: 10
Question Number 97803 Answers: 1 Comments: 0
Question Number 97606 Answers: 1 Comments: 0
Question Number 97478 Answers: 0 Comments: 0
Question Number 97129 Answers: 0 Comments: 0
Question Number 96764 Answers: 1 Comments: 5
Question Number 96761 Answers: 0 Comments: 0
Question Number 96671 Answers: 1 Comments: 0

Question Number 96667 Answers: 2 Comments: 0
Question Number 96358 Answers: 0 Comments: 0

Question Number 96290 Answers: 0 Comments: 1
