Question and Answers Forum

OthersQuestion and Answers: Page 65

Question Number 101250 Answers: 0 Comments: 0

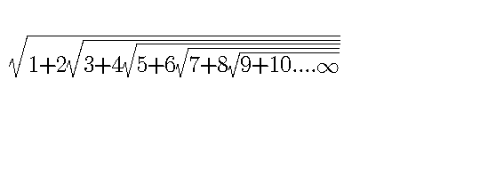
Question Number 101247 Answers: 1 Comments: 0

Question Number 101243 Answers: 0 Comments: 3

Find the solution xa^(1/x) +(1/x)a^x =2a a∈{−1,0,1} and also find when a is not given

$$\mathrm{Find}\:\mathrm{the}\:\mathrm{solution}\: \\ $$$$\:\:\mathrm{xa}^{\frac{\mathrm{1}}{\mathrm{x}}} +\frac{\mathrm{1}}{\mathrm{x}}\mathrm{a}^{\mathrm{x}} =\mathrm{2a}\:\:\:\mathrm{a}\in\left\{−\mathrm{1},\mathrm{0},\mathrm{1}\right\}\:\:\:{and}\:{also}\:{find}\:{when}\:{a}\:\:{is}\:{not}\:{given} \\ $$

Question Number 101231 Answers: 1 Comments: 1

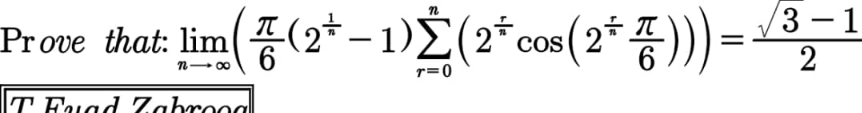
Question Number 101159 Answers: 1 Comments: 0

given the complex number z such that z−4i=a+3zi. find the value of a if z is purwly imaginary

$${given}\:{the}\:{complex}\:{number}\:{z}\:{such}\:{that} \\ $$$${z}−\mathrm{4}{i}={a}+\mathrm{3}{zi}.\: \\ $$$${find}\:{the}\:{value}\:{of}\:{a}\:{if}\:\:{z}\:{is}\:{purwly}\:{imaginary} \\ $$$$ \\ $$

Question Number 101026 Answers: 1 Comments: 0

lim_(x→∞) (x/e^( sinx −x) )

$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\frac{{x}}{{e}^{\:\mathrm{sin}{x}\:−{x}} } \\ $$

Question Number 100986 Answers: 0 Comments: 1

Question Number 100985 Answers: 0 Comments: 3

Question Number 100943 Answers: 1 Comments: 0

Determine the poles of the function; f(x)=((x^5 −1)/(x^3 −1))

$$\mathcal{D}\mathrm{etermine}\:\mathrm{the}\:\mathrm{poles}\:\mathrm{of}\:\mathrm{the}\:\mathrm{function}; \\ $$$$\mathrm{f}\left(\mathrm{x}\right)=\frac{\mathrm{x}^{\mathrm{5}} −\mathrm{1}}{\mathrm{x}^{\mathrm{3}} −\mathrm{1}} \\ $$

Question Number 100916 Answers: 1 Comments: 0

solve the eqution : ((2 + x)/(12 + 4x)) = ((1/2))^x .,x =2

$${solve}\:{the}\:{eqution}\:: \\ $$$$\frac{\mathrm{2}\:+\:{x}}{\mathrm{12}\:+\:\mathrm{4}{x}}\:=\:\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{{x}} \:\:\:\:\:\:\:.,{x}\:=\mathrm{2}\: \\ $$

Question Number 100904 Answers: 3 Comments: 3

lim_(n→∞) [(((n+1)(n+2)......3n)/n^(2n) )]^(1/n)

$$\mathrm{li}\underset{\mathrm{n}\rightarrow\infty} {\mathrm{m}}\left[\frac{\left({n}+\mathrm{1}\right)\left({n}+\mathrm{2}\right)......\mathrm{3}{n}}{{n}^{\mathrm{2}{n}} }\right]^{\frac{\mathrm{1}}{{n}}} \\ $$

Question Number 100785 Answers: 1 Comments: 0

Question Number 100744 Answers: 0 Comments: 17

Happy tau day to all !!! 28 june

$$\mathrm{Happy}\:\boldsymbol{\mathrm{tau}}\:\boldsymbol{\mathrm{day}}\:\boldsymbol{\mathrm{to}}\:\boldsymbol{\mathrm{all}}\:!!! \\ $$$$ \\ $$$$\mathrm{28}\:{june}\: \\ $$

Question Number 100624 Answers: 1 Comments: 3

Find the value of (√(2+(√(2+(√(2+(√2)))))))...∞ using cos function

$$\mathrm{Find}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:\sqrt{\mathrm{2}+\sqrt{\mathrm{2}+\sqrt{\mathrm{2}+\sqrt{\mathrm{2}}}}}...\infty\:\mathrm{using}\:\mathrm{cos}\:\mathrm{function} \\ $$

Question Number 100539 Answers: 0 Comments: 2

(−1)^n Σ_(n=1) ^∞ (3^n /n)

$$\left(−\mathrm{1}\right)^{{n}} \underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{3}^{{n}} }{{n}} \\ $$

Question Number 100442 Answers: 0 Comments: 5

Find the value of log(−2) {imaginary}

$$\mathrm{Find}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:\:\:\:\:\mathrm{log}\left(−\mathrm{2}\right)\:\:\left\{\mathrm{imaginary}\right\} \\ $$

Question Number 100482 Answers: 1 Comments: 0

(√(1(√(2(√(3(√(4(√(5(√(6(√7))))))))))))).....∞=???????

$$\sqrt{\mathrm{1}\sqrt{\mathrm{2}\sqrt{\mathrm{3}\sqrt{\mathrm{4}\sqrt{\mathrm{5}\sqrt{\mathrm{6}\sqrt{\mathrm{7}}}}}}}}.....\infty=??????? \\ $$

Question Number 100295 Answers: 0 Comments: 0

a relation R is defined on the set of real numbers by xRy if and only if x−y is a multiple of 3. show that R is transitive

$${a}\:{relation}\:{R}\:{is}\:{defined}\:{on}\:{the}\:{set}\:{of}\:{real} \\ $$$${numbers}\:{by}\:{xRy}\:{if}\:{and}\:{only}\:{if}\:{x}−{y}\:{is}\:{a}\: \\ $$$${multiple}\:{of}\:\mathrm{3}.\:{show}\:{that}\:{R}\:{is}\:{transitive} \\ $$

Question Number 100240 Answers: 2 Comments: 9

Find (x,y)∈R such that; ((x+y)/(x^2 −xy+y^2 ))=(7/2) updated from (2/7)→(7/2). Sorry, it was a mistake.

$$\mathrm{Find}\:\:\left(\mathrm{x},\mathrm{y}\right)\in\mathbb{R}\:\mathrm{such}\:\:\mathrm{that}; \\ $$$$\frac{\mathrm{x}+\mathrm{y}}{\mathrm{x}^{\mathrm{2}} −\mathrm{xy}+\mathrm{y}^{\mathrm{2}} }=\frac{\mathrm{7}}{\mathrm{2}} \\ $$$$ \\ $$$${updated}\:{from}\:\frac{\mathrm{2}}{\mathrm{7}}\rightarrow\frac{\mathrm{7}}{\mathrm{2}}.\:{Sorry},\:{it}\:{was}\:{a}\:{mistake}. \\ $$

Question Number 100097 Answers: 0 Comments: 1

∫(tanx)^e^(iπ) dx

$$\int\left({tanx}\right)^{{e}^{{i}\pi} } {dx} \\ $$

Question Number 100000 Answers: 2 Comments: 1

1+(1/(32))+(1/(243))+(1/(1024))+...∞

$$\mathrm{1}+\frac{\mathrm{1}}{\mathrm{32}}+\frac{\mathrm{1}}{\mathrm{243}}+\frac{\mathrm{1}}{\mathrm{1024}}+...\infty \\ $$

Question Number 99997 Answers: 0 Comments: 2

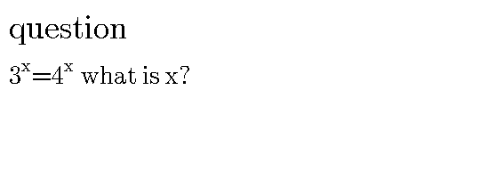
Question Number 99995 Answers: 0 Comments: 0

(√(1(√(3(√(5(√(7(√9)))))))))...∞

$$\sqrt{\mathrm{1}\sqrt{\mathrm{3}\sqrt{\mathrm{5}\sqrt{\mathrm{7}\sqrt{\mathrm{9}}}}}}...\infty \\ $$

Question Number 99994 Answers: 1 Comments: 0

1+(1/(16))+(1/(81))+(1/(256))+.....∞

$$\mathrm{1}+\frac{\mathrm{1}}{\mathrm{16}}+\frac{\mathrm{1}}{\mathrm{81}}+\frac{\mathrm{1}}{\mathrm{256}}+.....\infty \\ $$

Question Number 99975 Answers: 1 Comments: 0

((1/2))^(((1/3))^((1/4)....∞) ) =?

$$\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\left(\frac{\mathrm{1}}{\mathrm{3}}\right)^{\frac{\mathrm{1}}{\mathrm{4}}....\infty} } =? \\ $$

Question Number 99962 Answers: 1 Comments: 0

A particle Q moves in a plane and its polar coordinate (r,θ) are described by r = at^2 and θ = (1/3)t^4 find its speed at t = 2s

$$\mathrm{A}\:\mathrm{particle}\:{Q}\:\mathrm{moves}\:\mathrm{in}\:\mathrm{a}\:\mathrm{plane}\:\mathrm{and}\:\mathrm{its}\:\mathrm{polar}\:\mathrm{coordinate}\:\left({r},\theta\right) \\ $$$$\mathrm{are}\:\mathrm{described}\:\mathrm{by}\:{r}\:=\:{at}^{\mathrm{2}} \:\mathrm{and}\:\theta\:=\:\frac{\mathrm{1}}{\mathrm{3}}{t}^{\mathrm{4}} \:\mathrm{find}\:\mathrm{its} \\ $$$$\mathrm{speed}\:\mathrm{at}\:{t}\:=\:\mathrm{2s} \\ $$

Pg 60 Pg 61 Pg 62 Pg 63 Pg 64 Pg 65 Pg 66 Pg 67 Pg 68 Pg 69

Contact: info@tinkutara.com