
OthersQuestion and Answers: Page 64
Question Number 102085 Answers: 0 Comments: 0
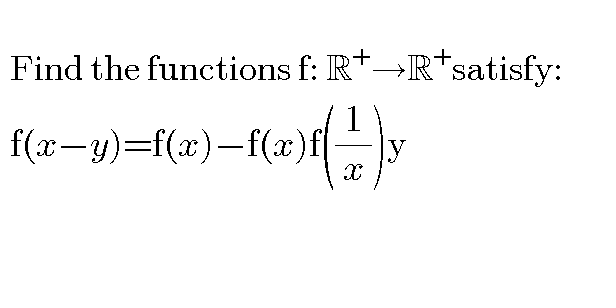
Question Number 102080 Answers: 0 Comments: 0
Question Number 102076 Answers: 0 Comments: 4
Question Number 101794 Answers: 1 Comments: 0
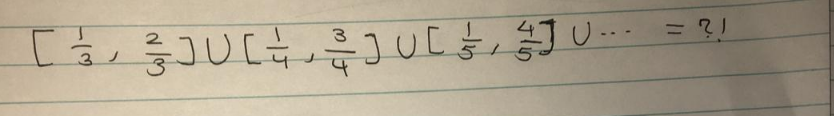
Question Number 101768 Answers: 0 Comments: 1
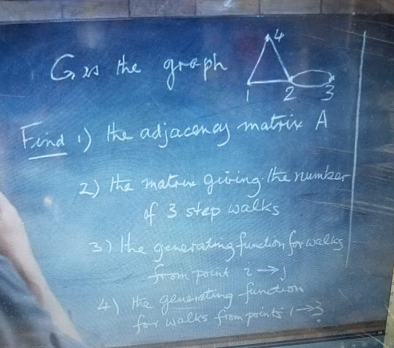
Question Number 101767 Answers: 0 Comments: 2

Question Number 101762 Answers: 0 Comments: 2

Question Number 101616 Answers: 2 Comments: 1

Question Number 101555 Answers: 1 Comments: 0

Question Number 101476 Answers: 1 Comments: 0
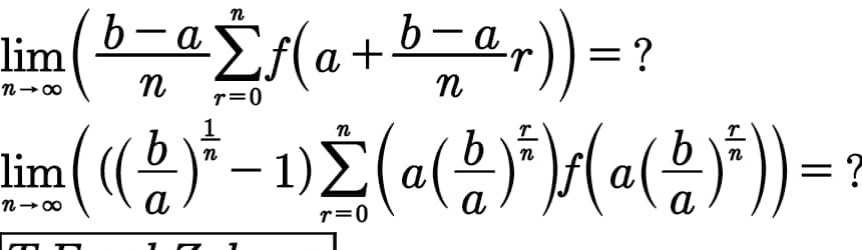
Question Number 101474 Answers: 1 Comments: 0

Question Number 101473 Answers: 1 Comments: 0

Question Number 101330 Answers: 0 Comments: 5
$${Evaluate}. \\ $$$$\int_{−\pi} ^{\pi} {x}^{\mathrm{9}} \mathrm{cos}\:{x}\:{dx} \\ $$
Question Number 101329 Answers: 1 Comments: 0

Question Number 101252 Answers: 0 Comments: 1
Question Number 101250 Answers: 0 Comments: 0
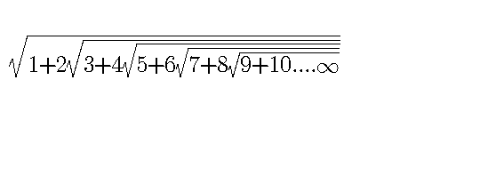
Question Number 101247 Answers: 1 Comments: 0

Question Number 101243 Answers: 0 Comments: 3
Question Number 101231 Answers: 1 Comments: 1
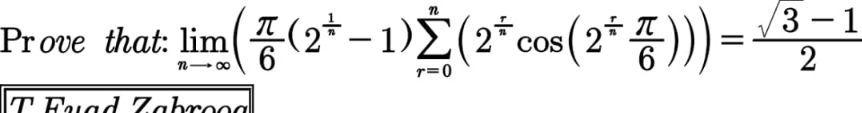
Question Number 101159 Answers: 1 Comments: 0
Question Number 101026 Answers: 1 Comments: 0
$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\frac{{x}}{{e}^{\:\mathrm{sin}{x}\:−{x}} } \\ $$
Question Number 100986 Answers: 0 Comments: 1

Question Number 100985 Answers: 0 Comments: 3

Question Number 100943 Answers: 1 Comments: 0
Question Number 100916 Answers: 1 Comments: 0
Question Number 100904 Answers: 3 Comments: 3
