
OthersQuestion and Answers: Page 63
Question Number 104207 Answers: 2 Comments: 0

Question Number 104199 Answers: 2 Comments: 0
Question Number 104174 Answers: 2 Comments: 0
Question Number 104173 Answers: 0 Comments: 0
Question Number 104333 Answers: 2 Comments: 0
Question Number 104176 Answers: 1 Comments: 0
Question Number 103808 Answers: 0 Comments: 1
Question Number 103669 Answers: 2 Comments: 0
Question Number 103574 Answers: 0 Comments: 0
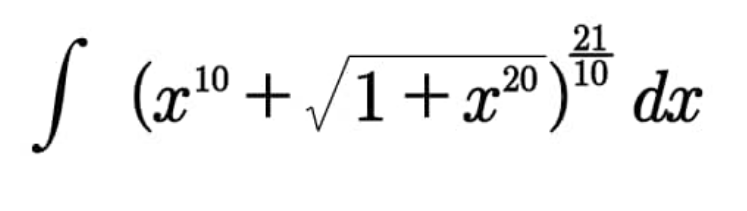
Question Number 103510 Answers: 1 Comments: 5

Question Number 103504 Answers: 0 Comments: 0

Question Number 103503 Answers: 2 Comments: 0
Question Number 103236 Answers: 0 Comments: 3
Question Number 103219 Answers: 1 Comments: 3
Question Number 103209 Answers: 3 Comments: 0

Question Number 103119 Answers: 0 Comments: 0
Question Number 103016 Answers: 0 Comments: 0

Question Number 103859 Answers: 1 Comments: 0
Question Number 102822 Answers: 1 Comments: 1
$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{n}!}{{n}^{{n}} } \\ $$
Question Number 102745 Answers: 0 Comments: 2
Question Number 102701 Answers: 2 Comments: 1
$${Evaluate}: \\ $$$$\int\frac{\mathrm{sin}\:{x}}{{x}}{dx} \\ $$
Question Number 102686 Answers: 0 Comments: 1
Question Number 102664 Answers: 2 Comments: 0
Question Number 102651 Answers: 0 Comments: 1
Question Number 102635 Answers: 2 Comments: 0

Question Number 102627 Answers: 3 Comments: 0
