
OthersQuestion and Answers: Page 62
Question Number 105130 Answers: 0 Comments: 0
Question Number 105080 Answers: 2 Comments: 0
Question Number 105075 Answers: 1 Comments: 0
Question Number 104975 Answers: 0 Comments: 2
Question Number 104948 Answers: 0 Comments: 0

Question Number 104940 Answers: 1 Comments: 1

Question Number 104789 Answers: 0 Comments: 1
Question Number 104783 Answers: 2 Comments: 0
Question Number 104777 Answers: 3 Comments: 0
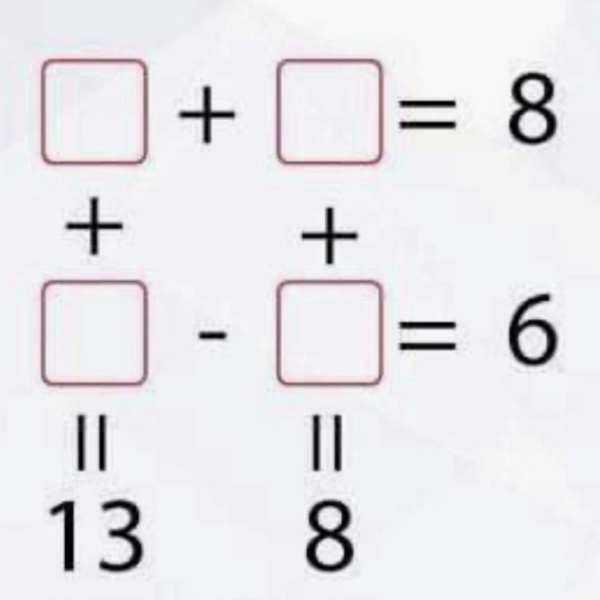
Question Number 104768 Answers: 1 Comments: 0
Question Number 104692 Answers: 2 Comments: 0

Question Number 104533 Answers: 3 Comments: 0
Question Number 104494 Answers: 0 Comments: 0

Question Number 104471 Answers: 1 Comments: 0
$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{e}^{{n}} {n}!}{{n}^{{n}} } \\ $$
Question Number 104406 Answers: 1 Comments: 1
Question Number 104296 Answers: 0 Comments: 0
Question Number 104207 Answers: 2 Comments: 0

Question Number 104199 Answers: 2 Comments: 0
Question Number 104174 Answers: 2 Comments: 0
Question Number 104173 Answers: 0 Comments: 0
Question Number 104333 Answers: 2 Comments: 0
Question Number 104176 Answers: 1 Comments: 0
Question Number 103808 Answers: 0 Comments: 1
Question Number 103669 Answers: 2 Comments: 0
Question Number 103574 Answers: 0 Comments: 0
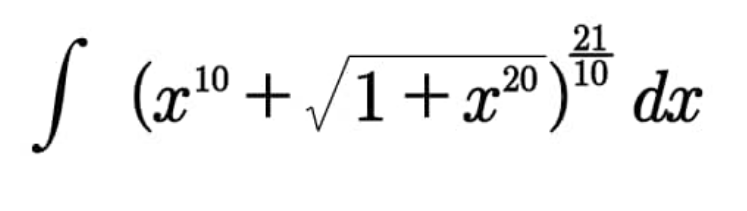
Question Number 103510 Answers: 1 Comments: 5

