Question and Answers Forum

All Questions   Topic List

OthersQuestion and Answers: Page 61

Question Number 107533    Answers: 2   Comments: 0

The position as a function of time x(t) for a particle in motion is given as x(t) = (3 m/s^2 )t^2 . Find the velocity of this particle as a function of time.

$$\mathrm{The}\:\mathrm{position}\:\:\mathrm{as}\:\mathrm{a}\:\mathrm{function}\:\mathrm{of}\:\mathrm{time}\:{x}\left({t}\right)\:\mathrm{for}\:\mathrm{a}\:\mathrm{particle}\:\mathrm{in} \\ $$$$\mathrm{motion}\:\mathrm{is}\:\mathrm{given}\:\mathrm{as}\:\:{x}\left({t}\right)\:=\:\left(\mathrm{3}\:\mathrm{m}/\mathrm{s}^{\mathrm{2}} \right){t}^{\mathrm{2}} \:.\:\mathrm{Find}\:\mathrm{the}\:\mathrm{velocity} \\ $$$$\mathrm{of}\:\mathrm{this}\:\mathrm{particle}\:\mathrm{as}\:\mathrm{a}\:\mathrm{function}\:\mathrm{of}\:\mathrm{time}. \\ $$

Question Number 107512    Answers: 0   Comments: 3

I seen that the function insert separator (right and left)don′t work,ask Titurkara fix this problem!

$$\mathrm{I}\:\mathrm{seen}\:\mathrm{that}\:\mathrm{the}\:\mathrm{function} \\ $$$$\mathrm{insert}\:\mathrm{separator}\:\left(\mathrm{right}\:\mathrm{and}\:\mathrm{left}\right)\mathrm{don}'\mathrm{t}\: \\ $$$$\mathrm{work},\mathrm{ask}\:\mathrm{Titurkara}\:\mathrm{fix}\:\mathrm{this}\:\mathrm{problem}! \\ $$

Question Number 107420    Answers: 1   Comments: 1

Question Number 107403    Answers: 0   Comments: 0

Question Number 107367    Answers: 0   Comments: 0

Question Number 107362    Answers: 0   Comments: 1

∫_0 ^∞ x^π e^(−x) dx

$$\int_{\mathrm{0}} ^{\infty} \mathrm{x}^{\pi} \mathrm{e}^{−\mathrm{x}} \mathrm{dx} \\ $$

Question Number 107353    Answers: 2   Comments: 0

If a b 13 c d 25 are six consecutive terms of an AP .find tbe value of a b c and d.

$${If}\:\mathrm{a}\:\mathrm{b}\:\mathrm{13}\:\mathrm{c}\:\mathrm{d}\:\mathrm{25}\:\mathrm{are}\:\mathrm{six}\:\mathrm{consecutive}\:\mathrm{terms}\:\mathrm{of}\:\mathrm{an}\:\mathrm{A}{P}\:.{find}\:{tbe}\:{value}\:{of}\:{a}\:{b}\:{c}\:{and}\:{d}. \\ $$

Question Number 107264    Answers: 2   Comments: 1

∫_0 ^∞ ⌊(1/x^2 )⌋dx

$$\int_{\mathrm{0}} ^{\infty} \lfloor\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }\rfloor\mathrm{dx} \\ $$

Question Number 107263    Answers: 0   Comments: 1

Σ_(n=1) ^n (√n)

$$\underset{\mathrm{n}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\sqrt{\mathrm{n}} \\ $$

Question Number 107187    Answers: 1   Comments: 3

Prove that (√8)=1+(3/4)+((3.5)/(4.8))+((3.5.7)/(4.8.12))+......

$$\mathrm{Prove}\:\mathrm{that} \\ $$$$\sqrt{\mathrm{8}}=\mathrm{1}+\frac{\mathrm{3}}{\mathrm{4}}+\frac{\mathrm{3}.\mathrm{5}}{\mathrm{4}.\mathrm{8}}+\frac{\mathrm{3}.\mathrm{5}.\mathrm{7}}{\mathrm{4}.\mathrm{8}.\mathrm{12}}+...... \\ $$

Question Number 107178    Answers: 1   Comments: 1

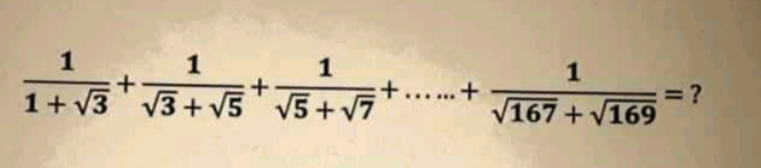
Question Number 107101    Answers: 0   Comments: 0

Fun time 1+2x+3x^2 +4x^3 +....=(1/((1−x)^2 )) 1+4+12+32+...=(1/((1−2)^2 )) 4+12+32+....=0 (No 1 fun) 5+11+17+23+...=0 Σ_(n=1) ^∞ 6n−1=6Σ_(n=1) ^∞ n−Σ^∞ 1=6.(−(1/(12)))−(−(1/2))=0 Σ^∞ n=−(1/(12)) (Ramanujan sum) Σ^∞ 1=1+1+1+1+1+...=−(1/2) Σ^∞ n^2 .Σ^∞ (1/n^2 )≥(Σ^∞ 1)^2 (Cauchy schwarz ineqality) Σ^∞ n^2 .(π^2 /6)≥(1/4) Σ^∞ n^2 ≥(3/(2π^2 ))

$$\mathrm{Fun}\:\mathrm{time} \\ $$$$ \\ $$$$\mathrm{1}+\mathrm{2x}+\mathrm{3x}^{\mathrm{2}} +\mathrm{4x}^{\mathrm{3}} +....=\frac{\mathrm{1}}{\left(\mathrm{1}−\mathrm{x}\right)^{\mathrm{2}} } \\ $$$$\mathrm{1}+\mathrm{4}+\mathrm{12}+\mathrm{32}+...=\frac{\mathrm{1}}{\left(\mathrm{1}−\mathrm{2}\right)^{\mathrm{2}} } \\ $$$$\mathrm{4}+\mathrm{12}+\mathrm{32}+....=\mathrm{0}\:\:\left(\mathrm{No}\:\mathrm{1}\:\mathrm{fun}\right) \\ $$$$ \\ $$$$\mathrm{5}+\mathrm{11}+\mathrm{17}+\mathrm{23}+...=\mathrm{0}\:\:\: \\ $$$$\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\mathrm{6n}−\mathrm{1}=\mathrm{6}\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\mathrm{n}−\overset{\infty} {\sum}\mathrm{1}=\mathrm{6}.\left(−\frac{\mathrm{1}}{\mathrm{12}}\right)−\left(−\frac{\mathrm{1}}{\mathrm{2}}\right)=\mathrm{0} \\ $$$$\overset{\infty} {\sum}\mathrm{n}=−\frac{\mathrm{1}}{\mathrm{12}}\:\:\:\:\left(\mathrm{Ramanujan}\:\mathrm{sum}\right) \\ $$$$\overset{\infty} {\sum}\mathrm{1}=\mathrm{1}+\mathrm{1}+\mathrm{1}+\mathrm{1}+\mathrm{1}+...=−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\overset{\infty} {\sum}\mathrm{n}^{\mathrm{2}} .\overset{\infty} {\sum}\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{2}} }\geqslant\left(\overset{\infty} {\sum}\mathrm{1}\right)^{\mathrm{2}} \:\:\:\left(\mathrm{Cauchy}\:\mathrm{schwarz}\:\mathrm{ineqality}\right) \\ $$$$\overset{\infty} {\sum}\mathrm{n}^{\mathrm{2}} .\frac{\pi^{\mathrm{2}} }{\mathrm{6}}\geqslant\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$\overset{\infty} {\sum}\mathrm{n}^{\mathrm{2}} \geqslant\frac{\mathrm{3}}{\mathrm{2}\pi^{\mathrm{2}} } \\ $$$$ \\ $$$$ \\ $$$$ \\ $$

Question Number 107092    Answers: 1   Comments: 2

Question Number 106828    Answers: 0   Comments: 2

∫ (1/(xdx)) is that true!

$$\:\int\:\frac{\mathrm{1}}{{xdx}}\:{is}\:{that}\:{true}! \\ $$

Question Number 106825    Answers: 5   Comments: 0

lim_(x→0) ((sin5x − tan5x)/x^3 )

$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{sin}\mathrm{5}{x}\:−\:{tan}\mathrm{5}{x}}{{x}^{\mathrm{3}} } \\ $$

Question Number 106694    Answers: 3   Comments: 0

Question Number 106653    Answers: 0   Comments: 7

30+144+420+960+1890+3360+...n

$$\mathrm{30}+\mathrm{144}+\mathrm{420}+\mathrm{960}+\mathrm{1890}+\mathrm{3360}+...{n} \\ $$

Question Number 106637    Answers: 1   Comments: 0

@JS@ The quartic equation x^4 +2x^3 +14x+15=0 has one root equal to 1+2i . Find the other three roots.

$$\:\:\:\:\:\:@\mathrm{JS}@ \\ $$$$\mathrm{The}\:\mathrm{quartic}\:\mathrm{equation}\:\mathrm{x}^{\mathrm{4}} +\mathrm{2x}^{\mathrm{3}} +\mathrm{14x}+\mathrm{15}=\mathrm{0} \\ $$$$\mathrm{has}\:\mathrm{one}\:\mathrm{root}\:\mathrm{equal}\:\mathrm{to}\:\mathrm{1}+\mathrm{2i}\:.\:\mathrm{Find} \\ $$$$\mathrm{the}\:\mathrm{other}\:\mathrm{three}\:\mathrm{roots}.\: \\ $$

Question Number 106630    Answers: 2   Comments: 0

Find n in this equation: (−2)^n = 4096

$${Find}\:{n}\:{in}\:{this}\:{equation}: \\ $$$$\left(−\mathrm{2}\right)^{{n}} \:=\:\mathrm{4096} \\ $$

Question Number 106526    Answers: 0   Comments: 2

Question Number 106503    Answers: 0   Comments: 11

(2/3)+(2/(18))+(2/(27))+(2/(324))+....

$$\frac{\mathrm{2}}{\mathrm{3}}+\frac{\mathrm{2}}{\mathrm{18}}+\frac{\mathrm{2}}{\mathrm{27}}+\frac{\mathrm{2}}{\mathrm{324}}+.... \\ $$

Question Number 106454    Answers: 0   Comments: 0

Question Number 106432    Answers: 0   Comments: 5

Question Number 106382    Answers: 0   Comments: 0

Question Number 106373    Answers: 1   Comments: 0

A ladder placed against a vertical walls ubtends an angle of 45 degree with thewall The distance between the footo f the ladder and the wall is 15mt calculae the length of the ladder correctto the nearest whole number.

$$ \\ $$$$\mathrm{A}\:\mathrm{ladder}\:\mathrm{placed}\:\mathrm{against}\:\mathrm{a}\:\mathrm{vertical}\:\mathrm{walls} \\ $$$$\mathrm{ubtends}\:\mathrm{an}\:\mathrm{angle}\:\mathrm{of}\:\mathrm{45}\:\mathrm{degree}\:\mathrm{with}\: \\ $$$$\mathrm{thewall}\:\mathrm{The}\:\mathrm{distance}\:\mathrm{between}\:\mathrm{the}\:\mathrm{footo} \\ $$$$\mathrm{f}\:\mathrm{the}\:\mathrm{ladder}\:\mathrm{and}\:\mathrm{the}\:\mathrm{wall}\:\mathrm{is}\:\mathrm{15mt} \\ $$$$\mathrm{calculae}\:\mathrm{the}\:\mathrm{length}\:\mathrm{of}\:\mathrm{the}\:\mathrm{ladder}\: \\ $$$$\mathrm{correctto}\:\mathrm{the}\:\mathrm{nearest}\:\mathrm{whole}\:\mathrm{number}. \\ $$

Question Number 106366    Answers: 1   Comments: 0

  Pg 56      Pg 57      Pg 58      Pg 59      Pg 60      Pg 61      Pg 62      Pg 63      Pg 64      Pg 65   

Terms of Service

Privacy Policy

Contact: [email protected]