Question and Answers Forum

OthersQuestion and Answers: Page 60

Question Number 106825 Answers: 5 Comments: 0

lim_(x→0) ((sin5x − tan5x)/x^3 )

$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{sin}\mathrm{5}{x}\:−\:{tan}\mathrm{5}{x}}{{x}^{\mathrm{3}} } \\ $$

Question Number 106694 Answers: 3 Comments: 0

Question Number 106653 Answers: 0 Comments: 7

30+144+420+960+1890+3360+...n

$$\mathrm{30}+\mathrm{144}+\mathrm{420}+\mathrm{960}+\mathrm{1890}+\mathrm{3360}+...{n} \\ $$

Question Number 106637 Answers: 1 Comments: 0

@JS@ The quartic equation x^4 +2x^3 +14x+15=0 has one root equal to 1+2i . Find the other three roots.

$$\:\:\:\:\:\:@\mathrm{JS}@ \\ $$$$\mathrm{The}\:\mathrm{quartic}\:\mathrm{equation}\:\mathrm{x}^{\mathrm{4}} +\mathrm{2x}^{\mathrm{3}} +\mathrm{14x}+\mathrm{15}=\mathrm{0} \\ $$$$\mathrm{has}\:\mathrm{one}\:\mathrm{root}\:\mathrm{equal}\:\mathrm{to}\:\mathrm{1}+\mathrm{2i}\:.\:\mathrm{Find} \\ $$$$\mathrm{the}\:\mathrm{other}\:\mathrm{three}\:\mathrm{roots}.\: \\ $$

Question Number 106630 Answers: 2 Comments: 0

Find n in this equation: (−2)^n = 4096

$${Find}\:{n}\:{in}\:{this}\:{equation}: \\ $$$$\left(−\mathrm{2}\right)^{{n}} \:=\:\mathrm{4096} \\ $$

Question Number 106526 Answers: 0 Comments: 2

Question Number 106503 Answers: 0 Comments: 11

(2/3)+(2/(18))+(2/(27))+(2/(324))+....

$$\frac{\mathrm{2}}{\mathrm{3}}+\frac{\mathrm{2}}{\mathrm{18}}+\frac{\mathrm{2}}{\mathrm{27}}+\frac{\mathrm{2}}{\mathrm{324}}+.... \\ $$

Question Number 106454 Answers: 0 Comments: 0

Question Number 106432 Answers: 0 Comments: 5

Question Number 106382 Answers: 0 Comments: 0

Question Number 106373 Answers: 1 Comments: 0

A ladder placed against a vertical walls ubtends an angle of 45 degree with thewall The distance between the footo f the ladder and the wall is 15mt calculae the length of the ladder correctto the nearest whole number.

$$ \\ $$$$\mathrm{A}\:\mathrm{ladder}\:\mathrm{placed}\:\mathrm{against}\:\mathrm{a}\:\mathrm{vertical}\:\mathrm{walls} \\ $$$$\mathrm{ubtends}\:\mathrm{an}\:\mathrm{angle}\:\mathrm{of}\:\mathrm{45}\:\mathrm{degree}\:\mathrm{with}\: \\ $$$$\mathrm{thewall}\:\mathrm{The}\:\mathrm{distance}\:\mathrm{between}\:\mathrm{the}\:\mathrm{footo} \\ $$$$\mathrm{f}\:\mathrm{the}\:\mathrm{ladder}\:\mathrm{and}\:\mathrm{the}\:\mathrm{wall}\:\mathrm{is}\:\mathrm{15mt} \\ $$$$\mathrm{calculae}\:\mathrm{the}\:\mathrm{length}\:\mathrm{of}\:\mathrm{the}\:\mathrm{ladder}\: \\ $$$$\mathrm{correctto}\:\mathrm{the}\:\mathrm{nearest}\:\mathrm{whole}\:\mathrm{number}. \\ $$

Question Number 106366 Answers: 1 Comments: 0

Question Number 106363 Answers: 0 Comments: 0

prove that : ⌊((√(10^(2k) −1))/3)⌋ = ((10^k −1)/3)

$${prove}\:{that}\:: \\ $$$$\lfloor\frac{\sqrt{\mathrm{10}^{\mathrm{2}{k}} −\mathrm{1}}}{\mathrm{3}}\rfloor\:=\:\frac{\mathrm{10}^{{k}} \:−\mathrm{1}}{\mathrm{3}} \\ $$$$ \\ $$

Question Number 106360 Answers: 0 Comments: 0

Question Number 106337 Answers: 3 Comments: 4

1+(5/2)+(9/4)+((13)/8)+((17)/(16))+......

$$\mathrm{1}+\frac{\mathrm{5}}{\mathrm{2}}+\frac{\mathrm{9}}{\mathrm{4}}+\frac{\mathrm{13}}{\mathrm{8}}+\frac{\mathrm{17}}{\mathrm{16}}+...... \\ $$

Question Number 106333 Answers: 0 Comments: 1

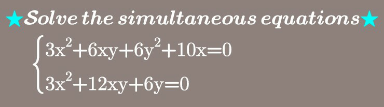
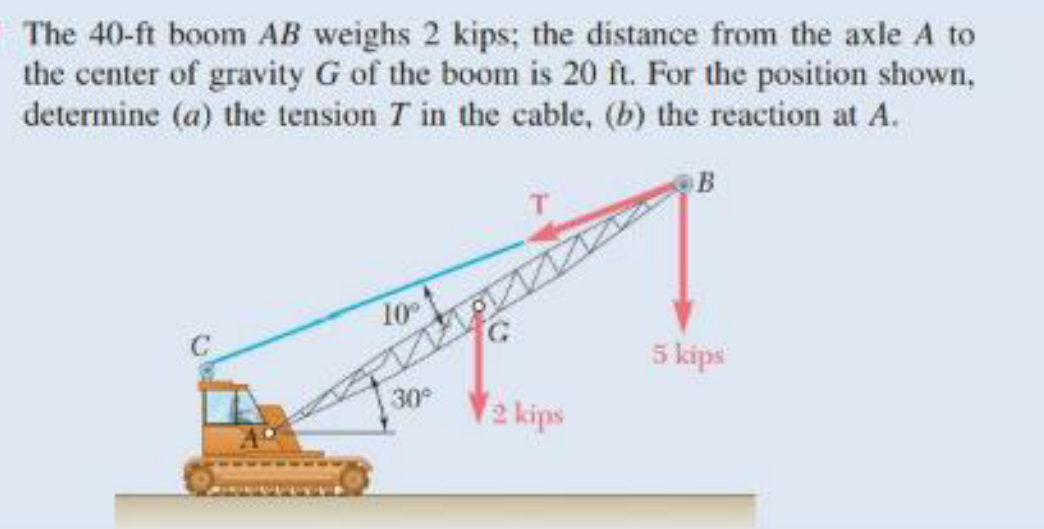
Question Number 106329 Answers: 2 Comments: 0

find ∫_(−5) ^5 ((√(25−x^2 )))dx whithout using trigonometric compensation

$${find}\:\int_{−\mathrm{5}} ^{\mathrm{5}} \left(\sqrt{\mathrm{25}−{x}^{\mathrm{2}} }\right){dx}\:\:{whithout}\:{using} \\ $$$${trigonometric}\:{compensation} \\ $$

Question Number 106318 Answers: 0 Comments: 0

∫_0 ^(log(2)) ((e^x −4)/(x +2))dx = ..... {(a)log(2) (b)1−log(2) (c) 1−2log(2) (d)−log(2)}

$$\int_{\mathrm{0}} ^{\mathrm{log}\left(\mathrm{2}\right)} \frac{{e}^{{x}} \:−\mathrm{4}}{{x}\:+\mathrm{2}}{dx}\:\:\:=\:..... \\ $$$$\left\{\left({a}\right){log}\left(\mathrm{2}\right)\:\:\:\:\:\:\:\left({b}\right)\mathrm{1}−{log}\left(\mathrm{2}\right)\:\:\:\:\:\:\:\left({c}\right)\right. \\ $$$$\left.\mathrm{1}−\mathrm{2}{log}\left(\mathrm{2}\right)\:\:\:\:\:\:\:\:\left({d}\right)−{log}\left(\mathrm{2}\right)\right\} \\ $$

Question Number 106163 Answers: 0 Comments: 0

Question Number 106039 Answers: 3 Comments: 0

if (f o g )(x) = x and f′(x)=1 + (f(x))^2 then g′(2) = ....

$${if}\:\:\left({f}\:{o}\:{g}\:\right)\left({x}\right)\:=\:{x}\:\:{and}\:{f}'\left({x}\right)=\mathrm{1}\:+\:\left({f}\left({x}\right)\right)^{\mathrm{2}} \\ $$$${then}\:{g}'\left(\mathrm{2}\right)\:=\:.... \\ $$$$ \\ $$

Question Number 105498 Answers: 1 Comments: 3

lim_(n→∞) (Π_(k=1) ^n ((1/k)))^(2/n)

$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:\left(\underset{{k}=\mathrm{1}} {\overset{{n}} {\prod}}\left(\frac{\mathrm{1}}{{k}}\right)\right)^{\frac{\mathrm{2}}{{n}}} \\ $$

Question Number 105488 Answers: 1 Comments: 0

if y = cos(x^2 ) then y^((n)) = .........

$${if}\:{y}\:=\:{cos}\left({x}^{\mathrm{2}} \right)\:\:\:\:\:\:{then}\: \\ $$$$\:\:\:\:\:\:{y}^{\left({n}\right)} \:=\:......... \\ $$

Question Number 105207 Answers: 1 Comments: 3

99−98((98)/(99)) = ? Can you solve this?

$$\mathrm{99}−\mathrm{98}\frac{\mathrm{98}}{\mathrm{99}}\:=\:? \\ $$$$\boldsymbol{{Can}}\:\boldsymbol{{you}}\:\boldsymbol{{solve}}\:\boldsymbol{{this}}? \\ $$

Question Number 105278 Answers: 1 Comments: 1

(1−(1/1))(1−(1/2))(1−(1/3)).....(1−(1/(100)))=?

$$\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{1}}\right)\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\right)\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{3}}\right).....\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{100}}\right)=? \\ $$

Question Number 105130 Answers: 0 Comments: 0

To now the real sequence in the follwing image : a_1 =1 ,a_2 =2 a_(nk +1) = ((a_(2k−1) +a_(2k) )/2) ∀ k ∈ Z^+ a_(2k+2) = (√(a_(2k) a_(2k+1) )) then prove that : lim_(n→∞) a_n = ((3(√3))/π)

$${To}\:{now}\:{the}\:{real}\:{sequence}\:{in}\:{the} \\ $$$${follwing}\:{image}\:: \\ $$$${a}_{\mathrm{1}} =\mathrm{1}\:\:\:,{a}_{\mathrm{2}} =\mathrm{2} \\ $$$${a}_{{nk}\:+\mathrm{1}} \:=\:\frac{{a}_{\mathrm{2}{k}−\mathrm{1}} \:+{a}_{\mathrm{2}{k}} }{\mathrm{2}}\:\:\:\:\:\:\:\:\:\:\:\forall\:{k}\:\in\:{Z}^{+} \\ $$$${a}_{\mathrm{2}{k}+\mathrm{2}} \:=\:\sqrt{{a}_{\mathrm{2}{k}} \:{a}_{\mathrm{2}{k}+\mathrm{1}} } \\ $$$${then}\: \\ $$$${prove}\:{that}\::\:\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:{a}_{{n}} \:=\:\frac{\mathrm{3}\sqrt{\mathrm{3}}}{\pi} \\ $$$$ \\ $$

Question Number 105080 Answers: 2 Comments: 0

solve: x((x^2 −1)!) = 5((x−1)!)

$${solve}: \\ $$$$\:{x}\left(\left({x}^{\mathrm{2}} −\mathrm{1}\right)!\right)\:=\:\mathrm{5}\left(\left({x}−\mathrm{1}\right)!\right) \\ $$

Pg 55 Pg 56 Pg 57 Pg 58 Pg 59 Pg 60 Pg 61 Pg 62 Pg 63 Pg 64

Contact: info@tinkutara.com