
OthersQuestion and Answers: Page 59
Question Number 112162 Answers: 1 Comments: 3

Question Number 111975 Answers: 1 Comments: 0

Question Number 111957 Answers: 0 Comments: 31
Question Number 111774 Answers: 1 Comments: 0

Question Number 111668 Answers: 0 Comments: 6

Question Number 111643 Answers: 1 Comments: 0
$$\left(\frac{\mathrm{7}}{\mathrm{3}}\right)!\left({with}\:{out}\:{calculator}\right) \\ $$
Question Number 111536 Answers: 2 Comments: 2
Question Number 111466 Answers: 1 Comments: 2
$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{n}^{{n}} }{{n}!} \\ $$
Question Number 111450 Answers: 0 Comments: 1

Question Number 111428 Answers: 0 Comments: 1
$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{n}^{\mathrm{3}} }{{n}!} \\ $$
Question Number 111132 Answers: 1 Comments: 0
Question Number 111152 Answers: 0 Comments: 0
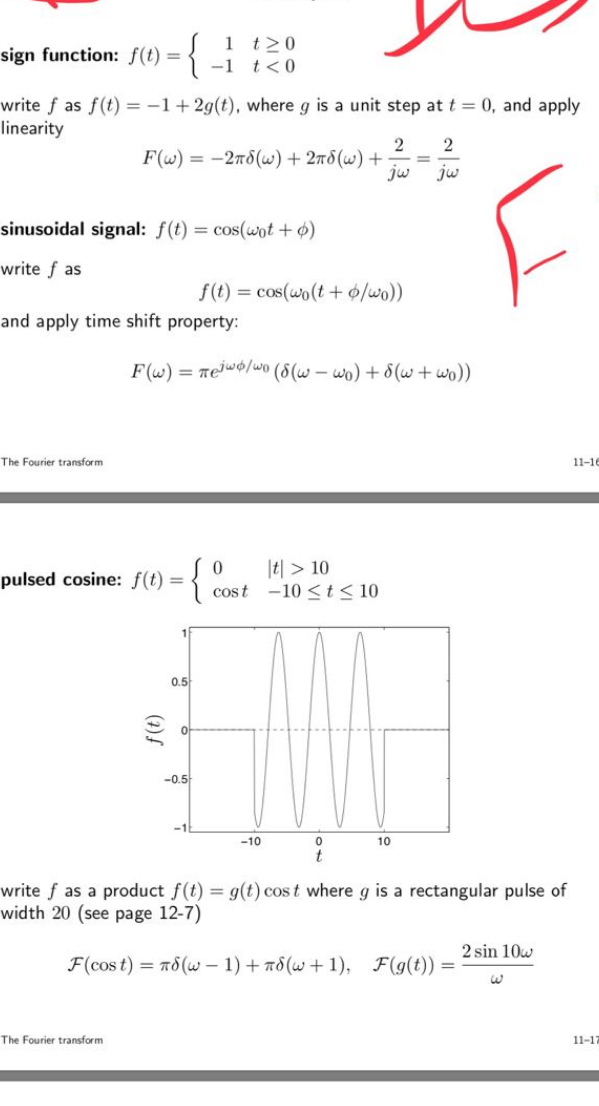
Question Number 111080 Answers: 1 Comments: 0
Question Number 110860 Answers: 1 Comments: 0

Question Number 110742 Answers: 0 Comments: 0
$${please}\:{give}\:{me}\:{a}\:{result}\:{of}\:{E}\left({tanx}\right) \\ $$
Question Number 110385 Answers: 0 Comments: 3

Question Number 110920 Answers: 1 Comments: 1

Question Number 110919 Answers: 1 Comments: 0
Question Number 109922 Answers: 1 Comments: 0
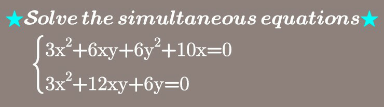
Question Number 109787 Answers: 0 Comments: 0
Question Number 109776 Answers: 0 Comments: 0
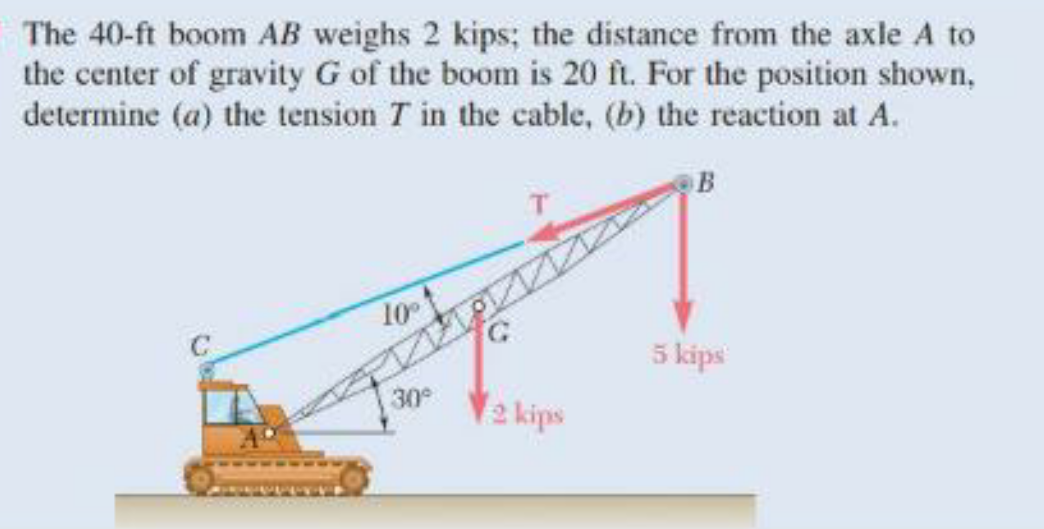
Question Number 109655 Answers: 0 Comments: 0

Question Number 109619 Answers: 0 Comments: 2
$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{n}!}{{n}^{{n}} } \\ $$
Question Number 109208 Answers: 1 Comments: 0
Question Number 109123 Answers: 0 Comments: 0
Question Number 109119 Answers: 2 Comments: 0
