Question and Answers Forum

OthersQuestion and Answers: Page 58

Question Number 116480 Answers: 1 Comments: 0

(1/8)+(1/(18))+(1/(30))+(1/(44))+(1/(60))+(1/(78))+(1/(98))+(1/(120))+........

$$\frac{\mathrm{1}}{\mathrm{8}}+\frac{\mathrm{1}}{\mathrm{18}}+\frac{\mathrm{1}}{\mathrm{30}}+\frac{\mathrm{1}}{\mathrm{44}}+\frac{\mathrm{1}}{\mathrm{60}}+\frac{\mathrm{1}}{\mathrm{78}}+\frac{\mathrm{1}}{\mathrm{98}}+\frac{\mathrm{1}}{\mathrm{120}}+........ \\ $$

Question Number 116443 Answers: 0 Comments: 0

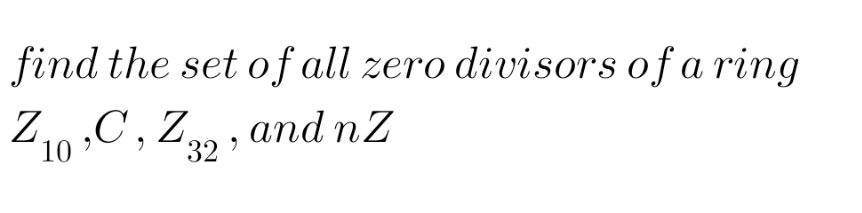
Question Number 116348 Answers: 1 Comments: 2

Find the minimum value of (((5+x)(2+x)^2 )/(x(1+x))) (x≠−1,0)

$$\mathrm{Find}\:\mathrm{the}\:\mathrm{minimum}\:\mathrm{value}\:\mathrm{of}\:\frac{\left(\mathrm{5}+\mathrm{x}\right)\left(\mathrm{2}+\mathrm{x}\right)^{\mathrm{2}} }{\mathrm{x}\left(\mathrm{1}+\mathrm{x}\right)}\:\:\left(\mathrm{x}\neq−\mathrm{1},\mathrm{0}\right) \\ $$

Question Number 115732 Answers: 0 Comments: 1

Question Number 115696 Answers: 0 Comments: 4

e^x =logx

$$\mathrm{e}^{\mathrm{x}} =\mathrm{logx} \\ $$

Question Number 115632 Answers: 1 Comments: 6

Question Number 115487 Answers: 0 Comments: 3

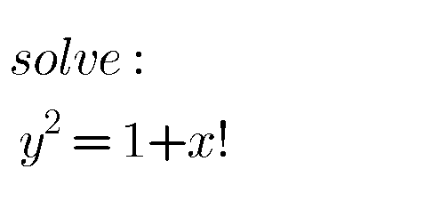
Question Number 115298 Answers: 1 Comments: 2

(d^2 y/dx^2 )+log(y)=0

$$\frac{\mathrm{d}^{\mathrm{2}} \mathrm{y}}{\mathrm{dx}^{\mathrm{2}} }+\mathrm{log}\left(\mathrm{y}\right)=\mathrm{0} \\ $$

Question Number 115285 Answers: 0 Comments: 0

...♠nice topology ♠... suppose ⟨S , τ ⟩ is Baire′s space and S = ∪_(n=1) ^∞ F_n such that F_n ′s are closed sets prove that:: ∃ m ; F_m ^( °) ≠ ∅ ..m.n.july ...♣m.n.july.1970♣...

$$\:\:\:\:\:\:\:\:...\spadesuit{nice}\:\:\:{topology}\:\spadesuit... \\ $$$${suppose}\:\:\langle{S}\:,\:\tau\:\rangle\:{is}\:\:{Baire}'{s} \\ $$$${space}\:\:\:{and}\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{S}\:=\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\cup}}{F}_{{n}} \:\:\:{such} \\ $$$${that}\:\:{F}_{{n}} '{s}\:\:{are}\:{closed}\:{sets}\: \\ $$$$\:\:\:\:{prove}\:\:{that}:: \\ $$$$\:\:\:\exists\:{m}\:;\:{F}_{{m}} ^{\:°} \:\neq\:\varnothing\:\:\:..{m}.{n}.{july} \\ $$$$\:\:\:\:\:\:\:\:\:...\clubsuit{m}.{n}.{july}.\mathrm{1970}\clubsuit... \\ $$

Question Number 115237 Answers: 2 Comments: 0

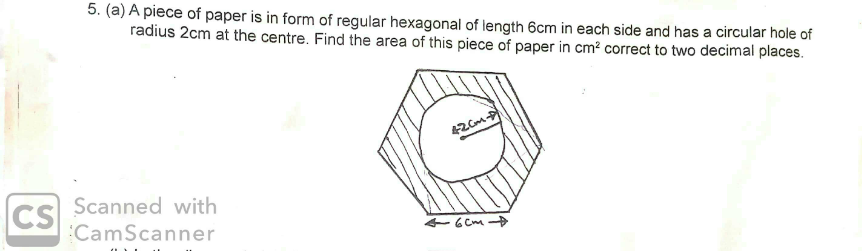
Question Number 115117 Answers: 1 Comments: 0

What is the value of a and b when 3x^4 +6x^3 −ax^2 −bx−12 is completely divisible by x^2 −3 ?

$${What}\:{is}\:{the}\:{value}\:{of}\:{a}\:{and}\:{b}\:{when}\: \\ $$$$\mathrm{3}{x}^{\mathrm{4}} +\mathrm{6}{x}^{\mathrm{3}} −{ax}^{\mathrm{2}} −{bx}−\mathrm{12}\:{is}\:{completely} \\ $$$${divisible}\:{by}\:{x}^{\mathrm{2}} −\mathrm{3}\:? \\ $$

Question Number 114682 Answers: 1 Comments: 0

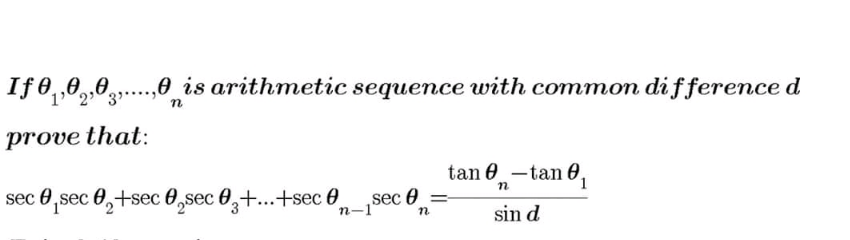
Question Number 114615 Answers: 1 Comments: 0

Question Number 114561 Answers: 1 Comments: 0

Question Number 114433 Answers: 1 Comments: 0

find sum of the series 1^2 −3^2 +5^2 −7^2 +9^2 −11^2 +...+(4n−3)^2 −(4n−1)^2

$${find}\:{sum}\:{of}\:{the}\:{series}\: \\ $$$$\mathrm{1}^{\mathrm{2}} −\mathrm{3}^{\mathrm{2}} +\mathrm{5}^{\mathrm{2}} −\mathrm{7}^{\mathrm{2}} +\mathrm{9}^{\mathrm{2}} −\mathrm{11}^{\mathrm{2}} +...+\left(\mathrm{4}{n}−\mathrm{3}\right)^{\mathrm{2}} −\left(\mathrm{4}{n}−\mathrm{1}\right)^{\mathrm{2}} \\ $$

Question Number 114343 Answers: 0 Comments: 4

How many ways can we place 5 identical books and another 6 identical books on a shelf?

$$\mathrm{How}\:\mathrm{many}\:\mathrm{ways}\:\mathrm{can}\:\mathrm{we}\:\mathrm{place}\:\mathrm{5}\:\mathrm{identical} \\ $$$$\mathrm{books}\:\mathrm{and}\:\mathrm{another}\:\mathrm{6}\:\mathrm{identical}\:\mathrm{books} \\ $$$$\mathrm{on}\:\mathrm{a}\:\mathrm{shelf}? \\ $$

Question Number 114032 Answers: 0 Comments: 0

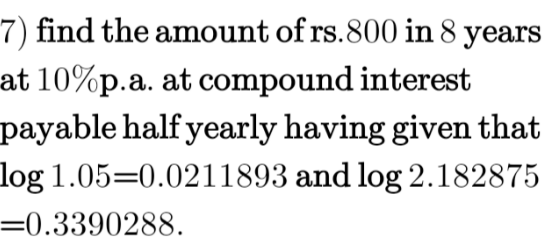
Question Number 113897 Answers: 1 Comments: 0

Question Number 113756 Answers: 2 Comments: 1

∫_0 ^1 ((log(x+1))/x)dx

$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{log}\left({x}+\mathrm{1}\right)}{{x}}{dx} \\ $$

Question Number 113637 Answers: 0 Comments: 0

Montrer que pour 0<z<1 on a Γ(z)Γ(1−z)=(π/(sin(πz)))

$${Montrer}\:{que}\:{pour}\:\mathrm{0}<{z}<\mathrm{1}\:{on}\:{a} \\ $$$$\Gamma\left({z}\right)\Gamma\left(\mathrm{1}−{z}\right)=\frac{\pi}{{sin}\left(\pi{z}\right)} \\ $$

Question Number 113499 Answers: 0 Comments: 0

Question Number 113490 Answers: 0 Comments: 1

Question Number 113456 Answers: 0 Comments: 0

Question Number 113455 Answers: 1 Comments: 1

Question Number 113354 Answers: 0 Comments: 3

( ((n),(0) )/2)−( ((n),(1) )/3)+( ((n),(2) )/4)−( ((n),(3) )/5)+.....n

$$\frac{\begin{pmatrix}{{n}}\\{\mathrm{0}}\end{pmatrix}}{\mathrm{2}}−\frac{\begin{pmatrix}{{n}}\\{\mathrm{1}}\end{pmatrix}}{\mathrm{3}}+\frac{\begin{pmatrix}{{n}}\\{\mathrm{2}}\end{pmatrix}}{\mathrm{4}}−\frac{\begin{pmatrix}{{n}}\\{\mathrm{3}}\end{pmatrix}}{\mathrm{5}}+.....{n} \\ $$

Question Number 113336 Answers: 0 Comments: 0

If 1, a^2 ,a^3 ,...,a^(n−1) are the roots nth of unity , prove that : (1+a)(1+a^2 )(1+a^3 )...(1+a^(n−1) ) = n−2⌊(n/2)⌋

$${If}\:\mathrm{1},\:{a}^{\mathrm{2}} ,{a}^{\mathrm{3}} \:,...,{a}^{{n}−\mathrm{1}} \:{are}\:{the}\:{roots}\: \\ $$$${nth}\:{of}\:{unity}\:,\: \\ $$$${prove}\:{that}\::\:\left(\mathrm{1}+{a}\right)\left(\mathrm{1}+{a}^{\mathrm{2}} \right)\left(\mathrm{1}+{a}^{\mathrm{3}} \right)...\left(\mathrm{1}+{a}^{{n}−\mathrm{1}} \right) \\ $$$$=\:{n}−\mathrm{2}\lfloor\frac{{n}}{\mathrm{2}}\rfloor \\ $$$$ \\ $$

Pg 53 Pg 54 Pg 55 Pg 56 Pg 57 Pg 58 Pg 59 Pg 60 Pg 61 Pg 62

Contact: info@tinkutara.com