
OthersQuestion and Answers: Page 54
Question Number 124528 Answers: 0 Comments: 0

Question Number 124487 Answers: 1 Comments: 1

Question Number 124474 Answers: 1 Comments: 1
Question Number 124461 Answers: 2 Comments: 2
$$\int_{\mathrm{0}} ^{\infty} {e}^{−{x}^{\mathrm{7}} } {sin}\left({x}^{\mathrm{7}} \right){dx} \\ $$
Question Number 124459 Answers: 1 Comments: 1
Question Number 124347 Answers: 1 Comments: 1

Question Number 124321 Answers: 2 Comments: 0
Question Number 124320 Answers: 2 Comments: 0
$${z}+\frac{\mathrm{1}}{{z}}=\mathrm{1} \\ $$$${z}^{\mathrm{3}} =?? \\ $$
Question Number 124300 Answers: 0 Comments: 0
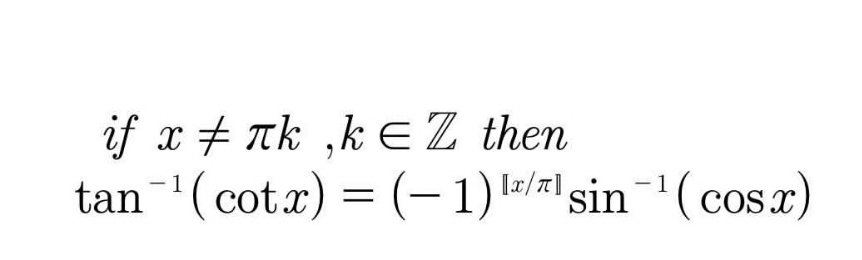
Question Number 124302 Answers: 1 Comments: 0
Question Number 124271 Answers: 0 Comments: 0

Question Number 124178 Answers: 1 Comments: 6
Question Number 123947 Answers: 0 Comments: 0
Question Number 123845 Answers: 1 Comments: 1

Question Number 123823 Answers: 1 Comments: 0

Question Number 123807 Answers: 0 Comments: 1
Question Number 123776 Answers: 0 Comments: 0
Question Number 123794 Answers: 0 Comments: 0
Question Number 123694 Answers: 0 Comments: 1
Question Number 123653 Answers: 1 Comments: 0

Question Number 123651 Answers: 1 Comments: 0
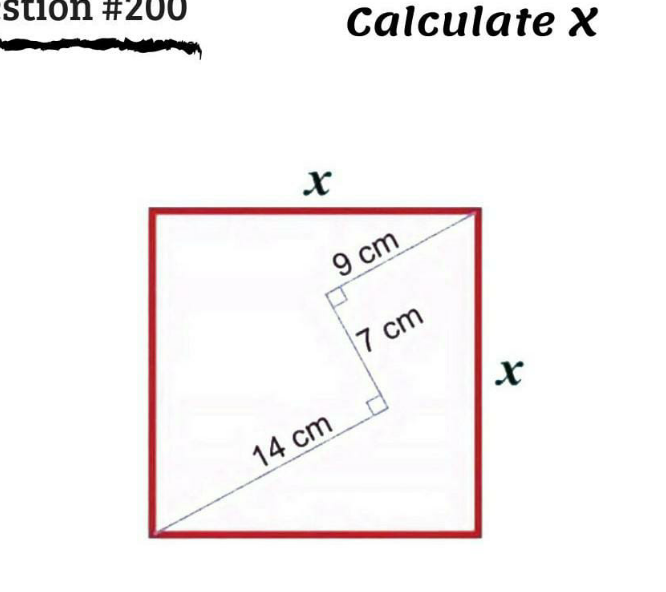
Question Number 123650 Answers: 0 Comments: 4
Question Number 123620 Answers: 0 Comments: 0
Question Number 123460 Answers: 0 Comments: 1
Question Number 123370 Answers: 0 Comments: 2
Question Number 123336 Answers: 1 Comments: 0
