
OthersQuestion and Answers: Page 53
Question Number 126669 Answers: 1 Comments: 2
Question Number 126632 Answers: 2 Comments: 1
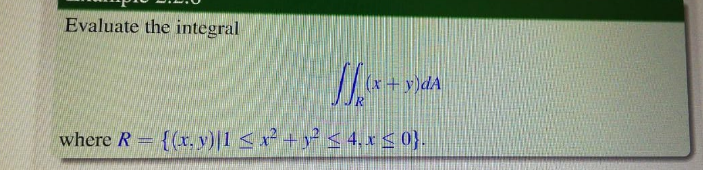
Question Number 126400 Answers: 1 Comments: 5
Question Number 126200 Answers: 0 Comments: 3
Question Number 126092 Answers: 2 Comments: 0
Question Number 125994 Answers: 1 Comments: 0
Question Number 127492 Answers: 0 Comments: 0
Question Number 125939 Answers: 0 Comments: 0
Question Number 125884 Answers: 0 Comments: 0
Question Number 125857 Answers: 1 Comments: 0
Question Number 125781 Answers: 0 Comments: 0
Question Number 125708 Answers: 1 Comments: 0
$$\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{1}−{tanhx}}{\:\sqrt[{\mathrm{5}}]{{tanhx}}}{dx} \\ $$
Question Number 125652 Answers: 0 Comments: 0

Question Number 125585 Answers: 0 Comments: 5
Question Number 125490 Answers: 0 Comments: 0
Question Number 125411 Answers: 0 Comments: 0
Question Number 125283 Answers: 0 Comments: 0
Question Number 125167 Answers: 0 Comments: 1
Question Number 125086 Answers: 0 Comments: 1

Question Number 125014 Answers: 0 Comments: 0

Question Number 124892 Answers: 0 Comments: 2
Question Number 124891 Answers: 0 Comments: 0
$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{24}}} {log}\left({tan}\theta\right){d}\theta \\ $$
Question Number 124861 Answers: 0 Comments: 0
Question Number 124718 Answers: 0 Comments: 1
Question Number 124642 Answers: 0 Comments: 0
Question Number 124595 Answers: 4 Comments: 0
