Question and Answers Forum

1+(1/(16))+(5^2 /(16^2 .2!))+((5^2 .9^2 )/(16^3 .3!))+((5^2 .9^2 .13^2 )/(16^4 .4!))+...=((√π)/(Γ^2 ((3/4))))=F_1 ((1/4),(1/4),1;1) Prove The above relation Where F_1 (Φ,ϕ,γ;μ)=Σ_(n≥0) ^∞ (((Φ)_n (ϕ)_n )/(n!(γ)_n ))μ^n (ζ)_n =ζ(ζ+1)(ζ+2)...(ζ+n−1)

$$\mathrm{1}+\frac{\mathrm{1}}{\mathrm{16}}+\frac{\mathrm{5}^{\mathrm{2}} }{\mathrm{16}^{\mathrm{2}} .\mathrm{2}!}+\frac{\mathrm{5}^{\mathrm{2}} .\mathrm{9}^{\mathrm{2}} }{\mathrm{16}^{\mathrm{3}} .\mathrm{3}!}+\frac{\mathrm{5}^{\mathrm{2}} .\mathrm{9}^{\mathrm{2}} .\mathrm{13}^{\mathrm{2}} }{\mathrm{16}^{\mathrm{4}} .\mathrm{4}!}+...=\frac{\sqrt{\pi}}{\Gamma^{\mathrm{2}} \left(\frac{\mathrm{3}}{\mathrm{4}}\right)}={F}_{\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{4}},\frac{\mathrm{1}}{\mathrm{4}},\mathrm{1};\mathrm{1}\right) \\ $$$${Prove}\:{The}\:{above}\:{relation} \\ $$$${Where} \\ $$$${F}_{\mathrm{1}} \left(\Phi,\varphi,\gamma;\mu\right)=\underset{{n}\geqslant\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(\Phi\right)_{{n}} \left(\varphi\right)_{{n}} }{{n}!\left(\gamma\right)_{{n}} }\mu^{{n}} \\ $$$$\left(\zeta\right)_{{n}} =\zeta\left(\zeta+\mathrm{1}\right)\left(\zeta+\mathrm{2}\right)...\left(\zeta+{n}−\mathrm{1}\right) \\ $$

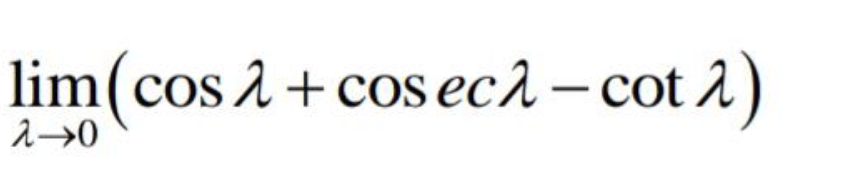
Question Number 128112 Answers: 3 Comments: 0

1 + 2 + 3 + 4 + ..... + 100 = ?

$$\:\mathrm{1}\:+\:\mathrm{2}\:+\:\mathrm{3}\:+\:\mathrm{4}\:+\:.....\:+\:\mathrm{100}\:=\:? \\ $$

Question Number 128110 Answers: 1 Comments: 0

∫_0 ^∞ ∫_0 ^∞ ((sinx sin(x+y))/(x(x+y)))dxdy

$$\int_{\mathrm{0}} ^{\infty} \int_{\mathrm{0}} ^{\infty} \frac{{sinx}\:{sin}\left({x}+{y}\right)}{{x}\left({x}+{y}\right)}{dxdy} \\ $$

Question Number 128093 Answers: 1 Comments: 0

Question Number 128083 Answers: 2 Comments: 0

((8 − i)/(3 − 2i)) If the expression above is rewritten in the form a + bi, where a and b are real numbers, what is the value of a? A. 2 B. (8/3) C. 3 D. ((11)/3)

$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{8}\:−\:{i}}{\mathrm{3}\:−\:\mathrm{2}{i}} \\ $$$$\:\mathrm{If}\:\mathrm{the}\:\mathrm{expression}\:\mathrm{above}\:\mathrm{is}\:\mathrm{rewritten}\: \\ $$$$\:\mathrm{in}\:\mathrm{the}\:\mathrm{form}\:{a}\:+\:{bi},\:\mathrm{where}\:{a}\:\mathrm{and}\:{b}\:\mathrm{are} \\ $$$$\:\mathrm{real}\:\mathrm{numbers},\:\mathrm{what}\:\mathrm{is}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:{a}? \\ $$$$\:\mathrm{A}.\:\mathrm{2} \\ $$$$\:\mathrm{B}.\:\frac{\mathrm{8}}{\mathrm{3}} \\ $$$$\:\mathrm{C}.\:\mathrm{3} \\ $$$$\:\mathrm{D}.\:\frac{\mathrm{11}}{\mathrm{3}} \\ $$

Question Number 128030 Answers: 1 Comments: 0

99 × 99 = 9801 999 × 999 = 998001 9999 × 9999 = 99980001 99999 × 99999 = ? 999999 × 999999 = ?

$$\:\mathrm{99}\:×\:\mathrm{99}\:=\:\mathrm{9801} \\ $$$$\:\mathrm{999}\:×\:\mathrm{999}\:=\:\mathrm{998001} \\ $$$$\:\mathrm{9999}\:×\:\mathrm{9999}\:=\:\mathrm{99980001} \\ $$$$\:\mathrm{99999}\:×\:\mathrm{99999}\:=\:? \\ $$$$\:\mathrm{999999}\:×\:\mathrm{999999}\:=\:? \\ $$

Question Number 128008 Answers: 1 Comments: 0

If 347.9823 = (3/P) + 4Q + 7R + (9/(10)) + (8/(100)) + (2/S) + (3/T) Then find the value of P + Q + R + S + T

$$\mathrm{If}\:\mathrm{347}.\mathrm{9823}\:=\:\frac{\mathrm{3}}{{P}}\:+\:\mathrm{4}{Q}\:+\:\mathrm{7}{R}\:+\:\frac{\mathrm{9}}{\mathrm{10}}\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\:\frac{\mathrm{8}}{\mathrm{100}}\:+\:\frac{\mathrm{2}}{{S}}\:+\:\frac{\mathrm{3}}{{T}} \\ $$$${Then}\:{find}\:{the}\:{value}\:{of}\: \\ $$$${P}\:+\:{Q}\:+\:{R}\:+\:{S}\:+\:{T} \\ $$

Question Number 128001 Answers: 1 Comments: 0

(x − a) (x − b) (x − c) ..... (x − z) = ?

$$\left(\mathrm{x}\:−\:\mathrm{a}\right)\:\left(\mathrm{x}\:−\:\mathrm{b}\right)\:\left(\mathrm{x}\:−\:\mathrm{c}\right)\:.....\:\left(\mathrm{x}\:−\:\mathrm{z}\right)\:=\:? \\ $$

Question Number 127974 Answers: 1 Comments: 1

θ^(••) +(g/l)sinθ=0 Exact form (May include elliptic integral)

$$\overset{\bullet\bullet} {\theta}+\frac{{g}}{{l}}{sin}\theta=\mathrm{0} \\ $$$${Exact}\:{form}\:\left({May}\:{include}\:{elliptic}\:{integral}\right) \\ $$

Pg 46 Pg 47 Pg 48 Pg 49 Pg 50 Pg 51 Pg 52 Pg 53 Pg 54 Pg 55

Contact: info@tinkutara.com