
OthersQuestion and Answers: Page 49
Question Number 131686 Answers: 1 Comments: 6
Question Number 131580 Answers: 0 Comments: 2
Question Number 131507 Answers: 1 Comments: 0
Question Number 131346 Answers: 0 Comments: 0

Question Number 131094 Answers: 1 Comments: 1
Question Number 131083 Answers: 0 Comments: 0
Question Number 130992 Answers: 1 Comments: 0
Question Number 131078 Answers: 0 Comments: 0
Question Number 130978 Answers: 1 Comments: 5

Question Number 130925 Answers: 2 Comments: 4
Question Number 130912 Answers: 0 Comments: 0
$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{sech}\left({n}\pi\right)}{{n}} \\ $$
Question Number 130849 Answers: 3 Comments: 1

Question Number 130754 Answers: 0 Comments: 0

Question Number 130752 Answers: 0 Comments: 0

Question Number 130748 Answers: 1 Comments: 0
Question Number 130604 Answers: 3 Comments: 0
Question Number 130555 Answers: 1 Comments: 0
Question Number 130549 Answers: 2 Comments: 0
Question Number 130449 Answers: 0 Comments: 0
Question Number 130415 Answers: 0 Comments: 1
Question Number 130399 Answers: 1 Comments: 0

Question Number 130369 Answers: 1 Comments: 0

Question Number 130370 Answers: 2 Comments: 0
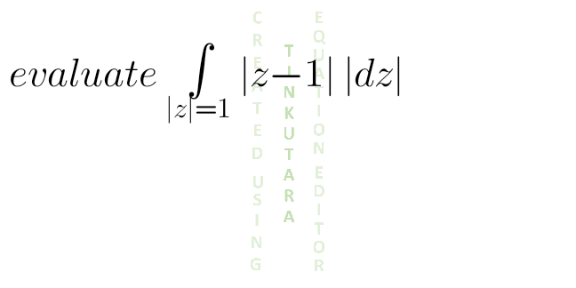
Question Number 130337 Answers: 2 Comments: 0
Question Number 130280 Answers: 0 Comments: 0
Question Number 130169 Answers: 1 Comments: 0
