
OthersQuestion and Answers: Page 47
Question Number 134941 Answers: 0 Comments: 1
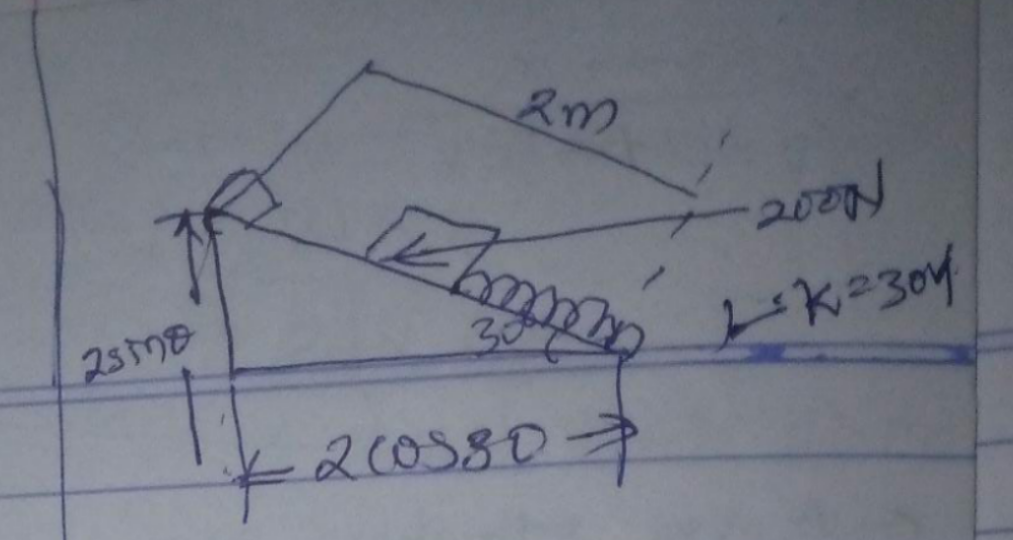
Question Number 134940 Answers: 0 Comments: 0
Question Number 134915 Answers: 1 Comments: 0

Question Number 134704 Answers: 1 Comments: 0

Question Number 134657 Answers: 0 Comments: 0
Question Number 134530 Answers: 1 Comments: 0
Question Number 134453 Answers: 0 Comments: 0

Question Number 134439 Answers: 1 Comments: 0
Question Number 134395 Answers: 0 Comments: 0

Question Number 134399 Answers: 0 Comments: 1

Question Number 134339 Answers: 0 Comments: 1
Question Number 134328 Answers: 1 Comments: 0
Question Number 134369 Answers: 1 Comments: 0

Question Number 134259 Answers: 0 Comments: 0
Question Number 134251 Answers: 0 Comments: 1
$$\underset{{n}=\mathrm{1}} {\overset{{n}} {\sum}}{nsin}\left({n}\right) \\ $$
Question Number 134135 Answers: 4 Comments: 0
Question Number 134117 Answers: 1 Comments: 0

Question Number 134002 Answers: 1 Comments: 1
Question Number 133988 Answers: 0 Comments: 2
Question Number 133838 Answers: 1 Comments: 1

Question Number 133722 Answers: 2 Comments: 0

Question Number 133708 Answers: 1 Comments: 0
Question Number 133692 Answers: 2 Comments: 1
Question Number 133590 Answers: 1 Comments: 0
Question Number 133482 Answers: 0 Comments: 1
Question Number 133432 Answers: 1 Comments: 0
