Question and Answers Forum

All Questions Topic List

OthersQuestion and Answers: Page 44

Question Number 138843 Answers: 0 Comments: 0

Question Number 138828 Answers: 1 Comments: 0

Question Number 138822 Answers: 0 Comments: 0

Question Number 138818 Answers: 0 Comments: 0

Question Number 138695 Answers: 0 Comments: 0

Question Number 138624 Answers: 0 Comments: 0

(1^π /(3!))+(2^π /(5!))+(3^π /(7!))+(4^π /(9!))+(5^π /(11!))+...

$$\frac{\mathrm{1}^{\pi} }{\mathrm{3}!}+\frac{\mathrm{2}^{\pi} }{\mathrm{5}!}+\frac{\mathrm{3}^{\pi} }{\mathrm{7}!}+\frac{\mathrm{4}^{\pi} }{\mathrm{9}!}+\frac{\mathrm{5}^{\pi} }{\mathrm{11}!}+... \\ $$

Question Number 138619 Answers: 0 Comments: 1

∫_0 ^∞ (e^(−x^(√3) ) −(1/((1+x^(√3) )^(√3) )))(dx/x)=(1/( (√3)))ψ((1/( (√3))))

$$\int_{\mathrm{0}} ^{\infty} \left({e}^{−{x}^{\sqrt{\mathrm{3}}} } −\frac{\mathrm{1}}{\left(\mathrm{1}+{x}^{\sqrt{\mathrm{3}}} \right)^{\sqrt{\mathrm{3}}} }\right)\frac{{dx}}{{x}}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\psi\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right) \\ $$

Question Number 138608 Answers: 0 Comments: 0

Prove or disprove ∫_0 ^a x^2 e^(−x^2 ) dx=(1/e^a^2 )((a^3 /(1.3))+((2a^5 )/(1.3.5))+((2a^7 )/(1.3.5.7))+((2a^9 )/(1.3.5.7.9))+ad inf..)

$${Prove}\:{or}\:{disprove} \\ $$$$\int_{\mathrm{0}} ^{{a}} {x}^{\mathrm{2}} {e}^{−{x}^{\mathrm{2}} } {dx}=\frac{\mathrm{1}}{{e}^{{a}^{\mathrm{2}} } }\left(\frac{{a}^{\mathrm{3}} }{\mathrm{1}.\mathrm{3}}+\frac{\mathrm{2}{a}^{\mathrm{5}} }{\mathrm{1}.\mathrm{3}.\mathrm{5}}+\frac{\mathrm{2}{a}^{\mathrm{7}} }{\mathrm{1}.\mathrm{3}.\mathrm{5}.\mathrm{7}}+\frac{\mathrm{2}{a}^{\mathrm{9}} }{\mathrm{1}.\mathrm{3}.\mathrm{5}.\mathrm{7}.\mathrm{9}}+{ad}\:{inf}..\right) \\ $$

Question Number 138569 Answers: 1 Comments: 0

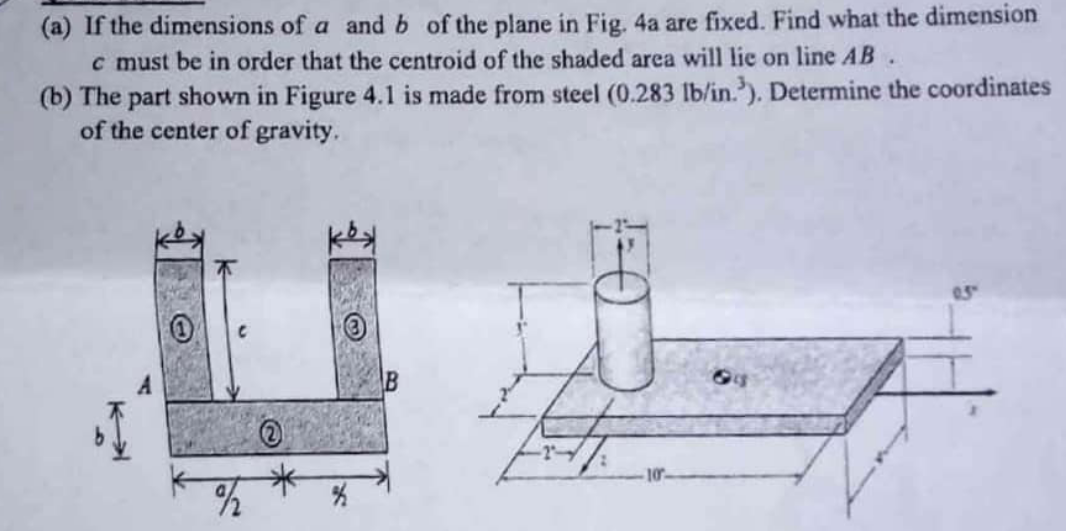
Question Number 138484 Answers: 0 Comments: 2

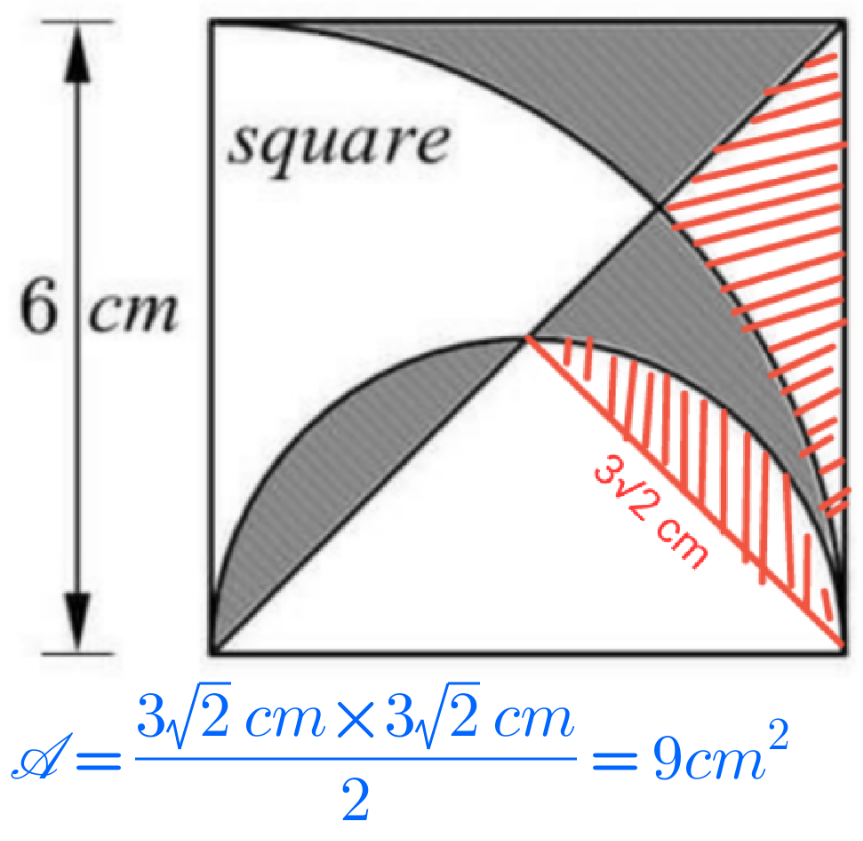
Question Number 138456 Answers: 1 Comments: 6

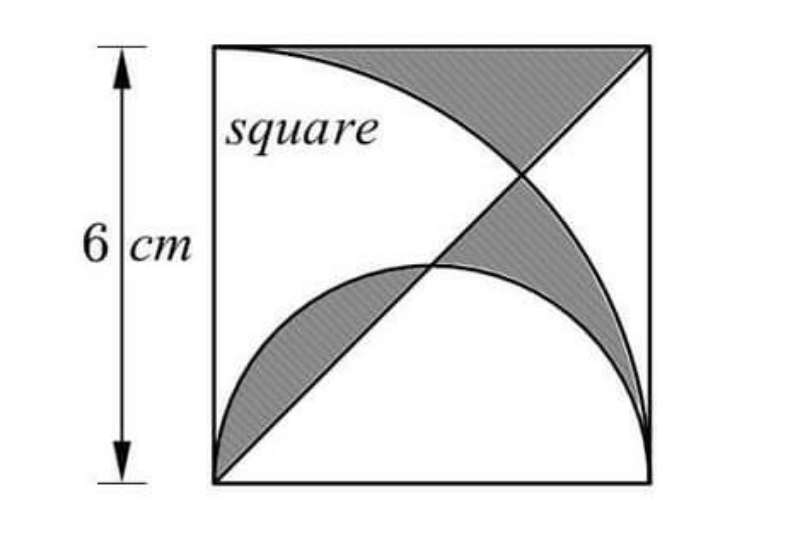
Question Number 138365 Answers: 1 Comments: 0

Question Number 138299 Answers: 2 Comments: 0

Question Number 138254 Answers: 0 Comments: 10

Question Number 138193 Answers: 1 Comments: 0

Given x≠y and x^2 =25x+y, y^2 =x+25y solve for the value of (√(x^2 +y^2 +1)) without using calculators or tools. Show your method.

$${Given}\:{x}\neq{y}\:{and}\:{x}^{\mathrm{2}} =\mathrm{25}{x}+{y},\:{y}^{\mathrm{2}} ={x}+\mathrm{25}{y}\: \\ $$$${solve}\:{for}\:{the}\:{value}\:{of}\:\sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} +\mathrm{1}}\:{without}\: \\ $$$${using}\:{calculators}\:{or}\:{tools}. \\ $$$${Show}\:{your}\:{method}. \\ $$

Question Number 138159 Answers: 1 Comments: 0

Question Number 138062 Answers: 2 Comments: 0

Question Number 138017 Answers: 0 Comments: 0

Question Number 137982 Answers: 5 Comments: 1

y^2 −x^2 =5(y−x)^2 . Find x:y

$${y}^{\mathrm{2}} −{x}^{\mathrm{2}} =\mathrm{5}\left({y}−{x}\right)^{\mathrm{2}} .\:{Find}\:{x}:{y} \\ $$

Question Number 137751 Answers: 0 Comments: 0

Question Number 137750 Answers: 0 Comments: 2

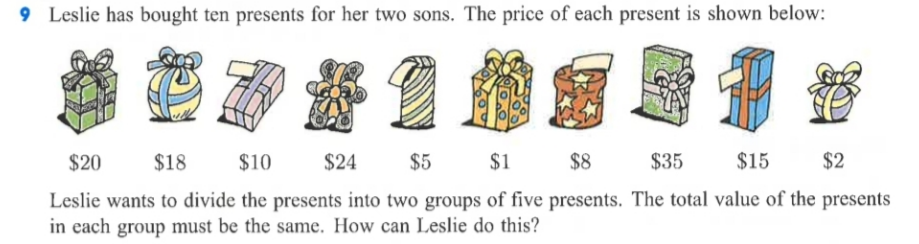
Question Number 137746 Answers: 1 Comments: 0

Question Number 137645 Answers: 1 Comments: 0

The sum of the squares of two consecutive odd numbers is 130. Find the larger number.

$${The}\:{sum}\:{of}\:{the}\:{squares}\:{of}\:{two}\:{consecutive} \\ $$$${odd}\:{numbers}\:{is}\:\mathrm{130}.\:{Find}\:{the}\:{larger}\:{number}. \\ $$

Question Number 137641 Answers: 1 Comments: 0

Question Number 137637 Answers: 0 Comments: 0

Prove or disprove ((cos(1+(1/( (√3))))𝛑)/1^2 )+((cos(1+(1/( (√3))))2π)/2^2 )+((cos(1+(1/( (√3))))3π)/3^2 )+...=0

$$\boldsymbol{\mathrm{Prove}}\:\boldsymbol{\mathrm{or}}\:\boldsymbol{\mathrm{disprove}} \\ $$$$\frac{{cos}\left(\mathrm{1}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)\boldsymbol{\pi}}{\mathrm{1}^{\mathrm{2}} }+\frac{{cos}\left(\mathrm{1}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)\mathrm{2}\pi}{\mathrm{2}^{\mathrm{2}} }+\frac{{cos}\left(\mathrm{1}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)\mathrm{3}\pi}{\mathrm{3}^{\mathrm{2}} }+...=\mathrm{0} \\ $$

Question Number 137634 Answers: 1 Comments: 0

x=2^(p ) and y=2^(q ) . Evaluate in terms of x and/ or y (i)2^(p+q) (ii) 2^(2q ) (iii) 2^(p−1)

$${x}=\mathrm{2}^{{p}\:} {and}\:{y}=\mathrm{2}^{{q}\:} .\:{Evaluate}\:{in}\:{terms}\:{of}\:{x}\:{and}/\:{or}\:{y}\: \\ $$$$\left({i}\right)\mathrm{2}^{{p}+{q}} \:\:\left({ii}\right)\:\mathrm{2}^{\mathrm{2}{q}\:} \:\:\:\left({iii}\right)\:\mathrm{2}^{{p}−\mathrm{1}} \\ $$

Pg 39 Pg 40 Pg 41 Pg 42 Pg 43 Pg 44 Pg 45 Pg 46 Pg 47 Pg 48

Terms of Service

Contact: info@tinkutara.com