Question and Answers Forum

OthersQuestion and Answers: Page 32

Question Number 169315 Answers: 1 Comments: 1

lim_(x→∞) (((1+(√(x+2)))/(1−(√(x+2))))) Mastermind

$${lim}_{{x}\rightarrow\infty} \left(\frac{\mathrm{1}+\sqrt{{x}+\mathrm{2}}}{\mathrm{1}−\sqrt{{x}+\mathrm{2}}}\right) \\ $$$$ \\ $$$${Mastermind} \\ $$

Question Number 169305 Answers: 4 Comments: 2

Differentiate the following wrt x 1) y=x^x 2) y=sin^(−1) (2x+1) Mastermind

$${Differentiate}\:{the}\:{following}\:{wrt}\:{x} \\ $$$$\left.\mathrm{1}\right)\:{y}={x}^{{x}} \\ $$$$\left.\mathrm{2}\right)\:{y}={sin}^{−\mathrm{1}} \left(\mathrm{2}{x}+\mathrm{1}\right) \\ $$$$ \\ $$$${Mastermind} \\ $$

Question Number 169303 Answers: 1 Comments: 1

Given that: x cos y=sin(x+y), find (dy/dx) Mastermind

$${Given}\:{that}: \\ $$$${x}\:{cos}\:{y}={sin}\left({x}+{y}\right),\:{find}\:\frac{{dy}}{{dx}} \\ $$$$ \\ $$$${Mastermind} \\ $$

Question Number 169200 Answers: 2 Comments: 0

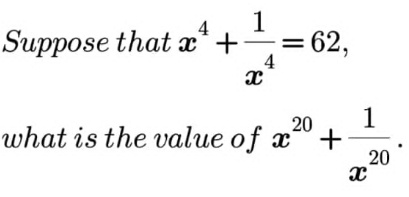
Question Number 169142 Answers: 2 Comments: 1

Question Number 168982 Answers: 1 Comments: 1

Question Number 168952 Answers: 1 Comments: 0

Question Number 168942 Answers: 0 Comments: 2

Question Number 168910 Answers: 0 Comments: 3

Resolve 1) (x−y)ydx−x^2 dy=0 2)(2x−y)dx+(4x−2y+3)dy=0

$${Resolve} \\ $$$$\left.\mathrm{1}\right)\:\left({x}−{y}\right){ydx}−{x}^{\mathrm{2}} {dy}=\mathrm{0} \\ $$$$\left.\mathrm{2}\right)\left(\mathrm{2}{x}−{y}\right){dx}+\left(\mathrm{4}{x}−\mathrm{2}{y}+\mathrm{3}\right){dy}=\mathrm{0} \\ $$

Question Number 168909 Answers: 0 Comments: 1

Resolve (1−x^2 y)dx+(x^2 y−x^3 )dy=0 ; μ=μ(x)

$${Resolve}\: \\ $$$$\left(\mathrm{1}−{x}^{\mathrm{2}} {y}\right){dx}+\left({x}^{\mathrm{2}} {y}−{x}^{\mathrm{3}} \right){dy}=\mathrm{0}\:;\:\mu=\mu\left({x}\right) \\ $$

Question Number 168868 Answers: 0 Comments: 0

Question Number 168842 Answers: 0 Comments: 0

Question Number 168841 Answers: 0 Comments: 0

Question Number 168744 Answers: 3 Comments: 0

Resolve 1) ∫((√(1+cos x))/(sin x))dx 2) ∫(dx/(1+((x+1))^(1/3) )) 3) ∫((xtan x)/(cos^4 x))dx 4) ∫(dx/(1+(√x)+(√(1+x))))

$${Resolve} \\ $$$$\left.\mathrm{1}\right)\:\int\frac{\sqrt{\mathrm{1}+\mathrm{cos}\:{x}}}{\mathrm{sin}\:{x}}{dx} \\ $$$$\left.\mathrm{2}\right)\:\int\frac{{dx}}{\mathrm{1}+\sqrt[{\mathrm{3}}]{{x}+\mathrm{1}}} \\ $$$$\left.\mathrm{3}\right)\:\int\frac{{x}\mathrm{tan}\:{x}}{\mathrm{cos}\:^{\mathrm{4}} {x}}{dx} \\ $$$$\left.\mathrm{4}\right)\:\int\frac{{dx}}{\mathrm{1}+\sqrt{{x}}+\sqrt{\mathrm{1}+{x}}} \\ $$

Question Number 168742 Answers: 1 Comments: 0

Resolve y=xy′+a(√(1+(y′)^2 ))

$${Resolve} \\ $$$${y}={xy}'+{a}\sqrt{\mathrm{1}+\left(\mathrm{y}'\right)^{\mathrm{2}} } \\ $$

Question Number 168723 Answers: 0 Comments: 2

Resolve (x+5)^5 y^(′′) =1

$${Resolve}\: \\ $$$$\left({x}+\mathrm{5}\right)^{\mathrm{5}} {y}^{''} =\mathrm{1} \\ $$

Question Number 168722 Answers: 0 Comments: 1

Resolve x^2 y^(′′) +xy^′ +y=1

$${Resolve}\: \\ $$$${x}^{\mathrm{2}} {y}^{''} +{xy}^{'} +{y}=\mathrm{1} \\ $$

Question Number 168679 Answers: 2 Comments: 0

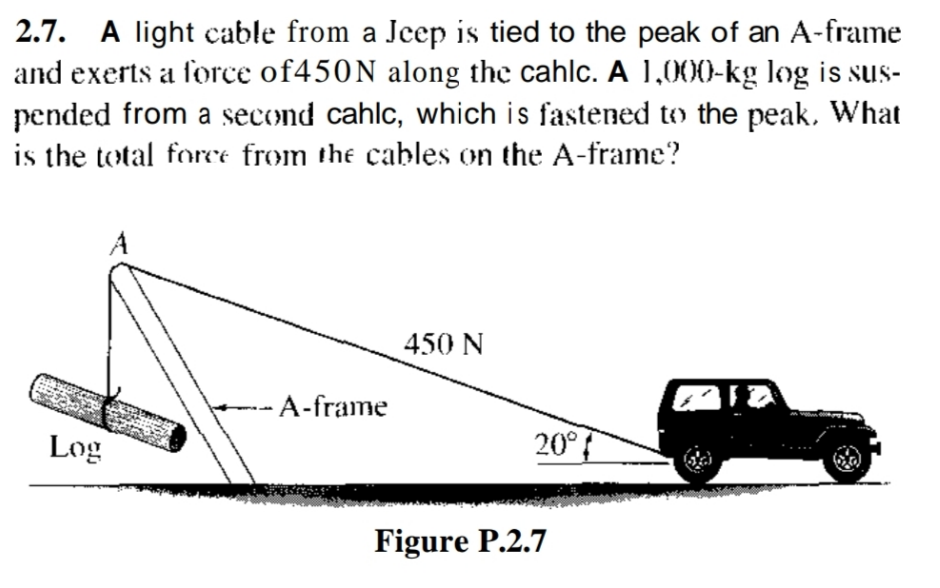
Question Number 168617 Answers: 0 Comments: 2

Question Number 168616 Answers: 1 Comments: 0

Question Number 168613 Answers: 3 Comments: 1

Resolve 1) x(dy/dx)−y=y^3 2) (x−y)ydx−x^2 dy=0 3) (2x−y)dx+(4x−2y+3)dy=0

$${Resolve}\: \\ $$$$\left.\mathrm{1}\right)\:{x}\frac{{dy}}{{dx}}−{y}={y}^{\mathrm{3}} \\ $$$$\left.\mathrm{2}\right)\:\left({x}−{y}\right){ydx}−{x}^{\mathrm{2}} {dy}=\mathrm{0} \\ $$$$\left.\mathrm{3}\right)\:\left(\mathrm{2}{x}−{y}\right){dx}+\left(\mathrm{4}{x}−\mathrm{2}{y}+\mathrm{3}\right){dy}=\mathrm{0} \\ $$

Question Number 168608 Answers: 2 Comments: 0

Question Number 168549 Answers: 1 Comments: 0

Resolve (x−2)^2 y^(′′) −3(x−2)y′+y=x

$${Resolve} \\ $$$$\left({x}−\mathrm{2}\right)^{\mathrm{2}} {y}^{''} −\mathrm{3}\left({x}−\mathrm{2}\right){y}'+{y}={x} \\ $$

Question Number 168548 Answers: 1 Comments: 0

Question Number 168546 Answers: 0 Comments: 0

Question Number 168538 Answers: 2 Comments: 0

Pg 27 Pg 28 Pg 29 Pg 30 Pg 31 Pg 32 Pg 33 Pg 34 Pg 35 Pg 36

Contact: info@tinkutara.com