
OthersQuestion and Answers: Page 28
Question Number 172450 Answers: 1 Comments: 0

Question Number 172404 Answers: 0 Comments: 2

Question Number 172391 Answers: 1 Comments: 0

Question Number 172321 Answers: 0 Comments: 0

Question Number 172287 Answers: 0 Comments: 0

Question Number 172281 Answers: 0 Comments: 0

Question Number 172252 Answers: 0 Comments: 0
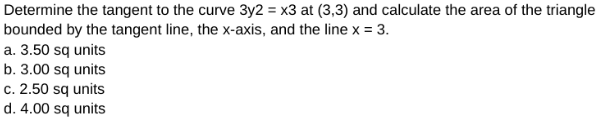
Question Number 172234 Answers: 1 Comments: 1

Question Number 172220 Answers: 0 Comments: 0
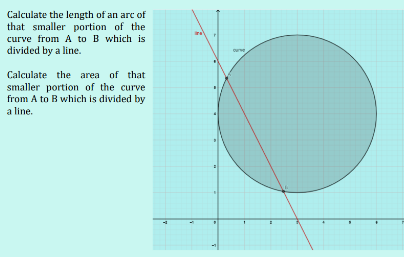
Question Number 172213 Answers: 0 Comments: 0
Question Number 172467 Answers: 0 Comments: 0

Question Number 172099 Answers: 1 Comments: 0
Question Number 172014 Answers: 0 Comments: 2
Question Number 171801 Answers: 1 Comments: 0
Question Number 171799 Answers: 0 Comments: 0
Question Number 171798 Answers: 0 Comments: 0
Question Number 171796 Answers: 0 Comments: 0
Question Number 171795 Answers: 0 Comments: 0
Question Number 171793 Answers: 0 Comments: 1

Question Number 171794 Answers: 0 Comments: 0
Question Number 171718 Answers: 0 Comments: 0

Question Number 171667 Answers: 1 Comments: 0

Question Number 171666 Answers: 0 Comments: 1
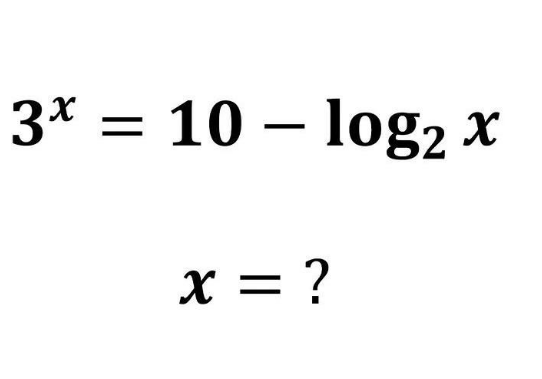
Question Number 171665 Answers: 1 Comments: 0
Question Number 171627 Answers: 0 Comments: 5
Question Number 171622 Answers: 0 Comments: 0

