
OthersQuestion and Answers: Page 25
Question Number 181568 Answers: 0 Comments: 0
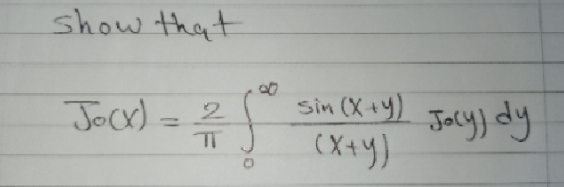
Question Number 178074 Answers: 0 Comments: 3
$${question}\:{posted}\:{by}\:{spillover}\:{in} \\ $$$$\mathrm{12}.\mathrm{10}.\mathrm{2022} \\ $$
Question Number 177957 Answers: 2 Comments: 0
Question Number 177922 Answers: 1 Comments: 0

Question Number 177870 Answers: 0 Comments: 0

Question Number 177859 Answers: 1 Comments: 0

Question Number 177835 Answers: 1 Comments: 0
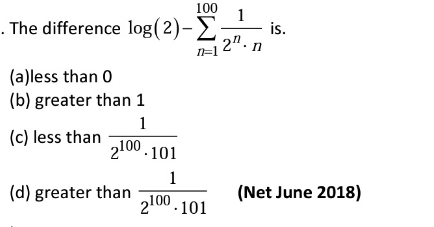
Question Number 177400 Answers: 3 Comments: 2
Question Number 177336 Answers: 0 Comments: 3
Question Number 177179 Answers: 1 Comments: 1
Question Number 177068 Answers: 1 Comments: 0
Question Number 176610 Answers: 1 Comments: 0

Question Number 176607 Answers: 1 Comments: 0

Question Number 176440 Answers: 0 Comments: 0

Question Number 176424 Answers: 0 Comments: 0
Question Number 176360 Answers: 0 Comments: 0

Question Number 176132 Answers: 0 Comments: 0

Question Number 176098 Answers: 1 Comments: 0
Question Number 176094 Answers: 0 Comments: 0

Question Number 176022 Answers: 0 Comments: 0
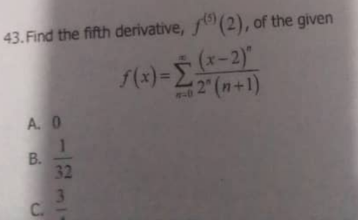
Question Number 176005 Answers: 0 Comments: 2

Question Number 175976 Answers: 1 Comments: 1

Question Number 175954 Answers: 0 Comments: 0

Question Number 175953 Answers: 1 Comments: 0

Question Number 175925 Answers: 1 Comments: 1
Question Number 175888 Answers: 1 Comments: 0
