
OthersQuestion and Answers: Page 21
Question Number 183600 Answers: 1 Comments: 3
Question Number 183465 Answers: 1 Comments: 0
Question Number 183464 Answers: 2 Comments: 0
Question Number 183211 Answers: 1 Comments: 0
Question Number 183210 Answers: 1 Comments: 0
Question Number 183209 Answers: 1 Comments: 0
Question Number 183117 Answers: 2 Comments: 0

Question Number 183101 Answers: 1 Comments: 3
Question Number 183073 Answers: 2 Comments: 0
Question Number 183135 Answers: 1 Comments: 0

Question Number 183039 Answers: 1 Comments: 0
Question Number 183038 Answers: 1 Comments: 0
Question Number 183036 Answers: 1 Comments: 0
Question Number 182984 Answers: 2 Comments: 0
Question Number 182941 Answers: 0 Comments: 0
Question Number 182934 Answers: 1 Comments: 0
Question Number 182810 Answers: 2 Comments: 0
Question Number 182803 Answers: 0 Comments: 0
Question Number 182779 Answers: 4 Comments: 1
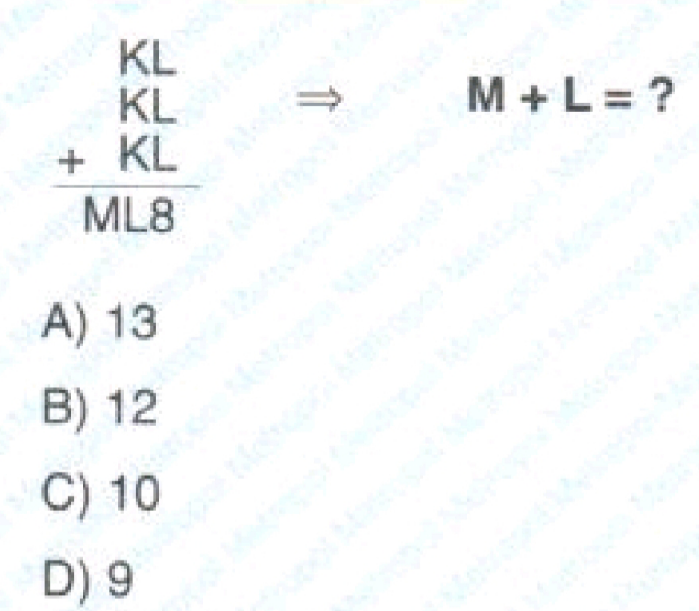
Question Number 182576 Answers: 0 Comments: 0

Question Number 182566 Answers: 0 Comments: 0
Question Number 182534 Answers: 1 Comments: 3
Question Number 182423 Answers: 4 Comments: 0

Question Number 182394 Answers: 1 Comments: 1

Question Number 182315 Answers: 0 Comments: 1

Question Number 182253 Answers: 0 Comments: 3

