
OthersQuestion and Answers: Page 20
Question Number 184656 Answers: 1 Comments: 0
Question Number 184655 Answers: 1 Comments: 0
Question Number 184574 Answers: 0 Comments: 5
Question Number 184497 Answers: 1 Comments: 0

Question Number 184487 Answers: 0 Comments: 1

Question Number 184454 Answers: 0 Comments: 1

Question Number 184320 Answers: 0 Comments: 4
Question Number 184311 Answers: 1 Comments: 0

Question Number 184307 Answers: 1 Comments: 0
Question Number 184306 Answers: 1 Comments: 0
Question Number 184264 Answers: 1 Comments: 0

Question Number 184218 Answers: 1 Comments: 0

Question Number 184188 Answers: 1 Comments: 0
Question Number 184187 Answers: 1 Comments: 0
Question Number 184185 Answers: 1 Comments: 0
Question Number 184184 Answers: 1 Comments: 0
$$\mathrm{y}=\left(\mathrm{sinx}\right)^{\mathrm{x}} \\ $$$$ \\ $$$$\mathrm{Differentiate} \\ $$
Question Number 184126 Answers: 1 Comments: 0
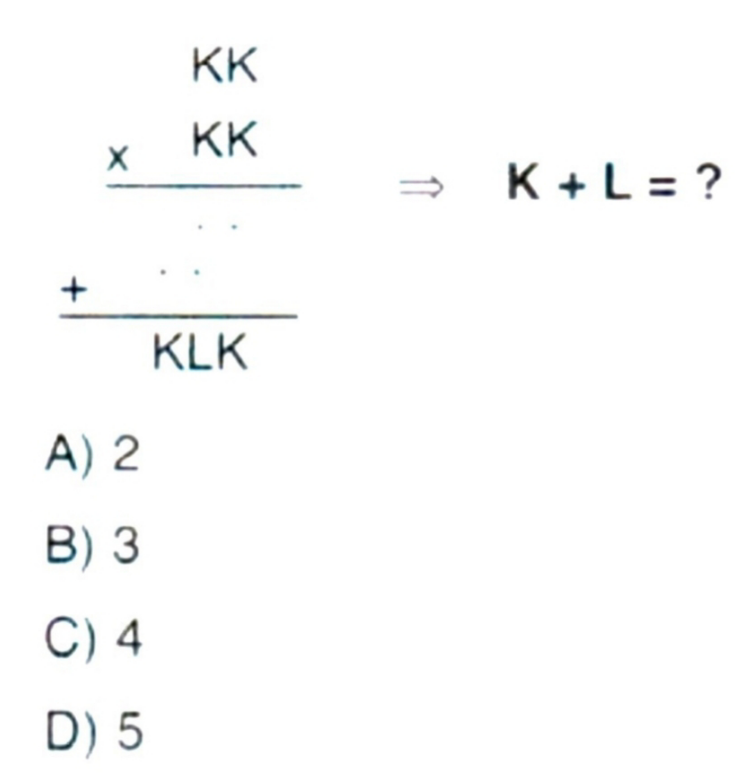
Question Number 184125 Answers: 0 Comments: 0

Question Number 184048 Answers: 5 Comments: 0
Question Number 184030 Answers: 1 Comments: 0
Question Number 184028 Answers: 0 Comments: 0
Question Number 184010 Answers: 0 Comments: 3
Question Number 183913 Answers: 0 Comments: 0

Question Number 183737 Answers: 2 Comments: 0
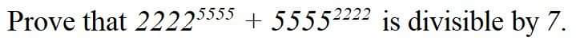
Question Number 183687 Answers: 3 Comments: 0
Question Number 183667 Answers: 0 Comments: 8
