Question and Answers Forum

OthersQuestion and Answers: Page 19

Question Number 181219 Answers: 1 Comments: 0

Solve the D.E x(dy/dx)−y=(√(x^2 +y^2 )) .

$$\mathrm{Solve}\:\mathrm{the}\:\mathrm{D}.\mathrm{E} \\ $$$$\mathrm{x}\frac{\mathrm{dy}}{\mathrm{dx}}−\mathrm{y}=\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} } \\ $$$$ \\ $$$$. \\ $$

Question Number 181218 Answers: 1 Comments: 0

Solve the Differential equation: x(dy/dx)−y=2y(lnx−lny) .

$$\mathrm{Solve}\:\mathrm{the}\:\mathrm{Differential}\:\mathrm{equation}: \\ $$$$\mathrm{x}\frac{\mathrm{dy}}{\mathrm{dx}}−\mathrm{y}=\mathrm{2y}\left(\mathrm{lnx}−\mathrm{lny}\right) \\ $$$$ \\ $$$$. \\ $$

Question Number 181217 Answers: 1 Comments: 0

Question Number 181023 Answers: 1 Comments: 0

Question Number 181245 Answers: 1 Comments: 7

(x−(1/x))(x^(4/3) +x^(2/3) )=x^(1/3) (x^2 −(1/x^2 )) prove LHS=RHS

$$\left(\mathrm{x}−\frac{\mathrm{1}}{\mathrm{x}}\right)\left(\mathrm{x}^{\frac{\mathrm{4}}{\mathrm{3}}} +\mathrm{x}^{\frac{\mathrm{2}}{\mathrm{3}}} \right)=\mathrm{x}^{\frac{\mathrm{1}}{\mathrm{3}}} \left(\mathrm{x}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }\right) \\ $$$$ \\ $$$$\mathrm{prove}\:\mathrm{LHS}=\mathrm{RHS} \\ $$

Question Number 181015 Answers: 1 Comments: 0

If z=xy−7x+4y, evaluate (∂z/(∂x )) and (∂z/∂y) .

$$\mathrm{If}\:\mathrm{z}=\mathrm{xy}−\mathrm{7x}+\mathrm{4y},\:\:\:\mathrm{evaluate}\:\frac{\partial\mathrm{z}}{\partial\mathrm{x}\:}\:\mathrm{and}\:\frac{\partial\mathrm{z}}{\partial\mathrm{y}} \\ $$$$ \\ $$$$. \\ $$$$ \\ $$

Question Number 181014 Answers: 0 Comments: 5

If f(x)=3−x^2 , find ((f(3+h)−f(3))/h) .

$$\mathrm{If}\:\mathrm{f}\left(\mathrm{x}\right)=\mathrm{3}−\mathrm{x}^{\mathrm{2}} ,\:\:\:\:\mathrm{find}\:\frac{\mathrm{f}\left(\mathrm{3}+\mathrm{h}\right)−\mathrm{f}\left(\mathrm{3}\right)}{\mathrm{h}} \\ $$$$ \\ $$$$. \\ $$

Question Number 180976 Answers: 2 Comments: 0

(dy/dx)=((x−y−2)/(x+y+6)) solve

$$\frac{\mathrm{dy}}{\mathrm{dx}}=\frac{\mathrm{x}−\mathrm{y}−\mathrm{2}}{\mathrm{x}+\mathrm{y}+\mathrm{6}} \\ $$$$ \\ $$$$\mathrm{solve} \\ $$

Question Number 180954 Answers: 1 Comments: 0

A tugboat is travelling from Asaba to Onitsha across the River Niger with a resultant velocity of 20 knots. If the river flows at 12 knots, the direction of motion of the boat relative to the direction of water flow is?

Question Number 180926 Answers: 0 Comments: 9

For this problem, we define the fractional part of x∈R_(≥0) as {x} = x − ⌊x⌋ where ⌊x⌋ is the integer part of x, i.e the greatest integer less than or equal to x. (a) Draw the function {x} in a cordinate system for 0≤x≤3 (b) Find the area A_n , under the graph of {x} between 0 and n∈N as given by A_n =∫_0 ^n {x}dx. M.m

$$\mathrm{For}\:\mathrm{this}\:\mathrm{problem},\:\mathrm{we}\:\mathrm{define}\:\mathrm{the}\: \\ $$$$\mathrm{fractional}\:\mathrm{part}\:\mathrm{of}\:\mathrm{x}\in\mathbb{R}_{\geqslant\mathrm{0}} \:\mathrm{as} \\ $$$$\left\{\mathrm{x}\right\}\:=\:\mathrm{x}\:−\:\lfloor\mathrm{x}\rfloor \\ $$$$\mathrm{where}\:\lfloor\mathrm{x}\rfloor\:\mathrm{is}\:\mathrm{the}\:\mathrm{integer}\:\mathrm{part}\:\mathrm{of}\:\mathrm{x},\:\mathrm{i}.\mathrm{e} \\ $$$$\mathrm{the}\:\mathrm{greatest}\:\mathrm{integer}\:\mathrm{less}\:\mathrm{than}\:\mathrm{or}\:\mathrm{equal} \\ $$$$\mathrm{to}\:\mathrm{x}. \\ $$$$\left(\mathrm{a}\right)\:\mathrm{Draw}\:\mathrm{the}\:\mathrm{function}\:\left\{\mathrm{x}\right\}\:\mathrm{in}\:\mathrm{a}\:\mathrm{cordinate} \\ $$$$\mathrm{system}\:\mathrm{for}\:\mathrm{0}\leqslant\mathrm{x}\leqslant\mathrm{3} \\ $$$$\left(\mathrm{b}\right)\:\mathrm{Find}\:\mathrm{the}\:\mathrm{area}\:\mathrm{A}_{\mathrm{n}} \:,\:\mathrm{under}\:\mathrm{the}\:\mathrm{graph} \\ $$$$\mathrm{of}\:\left\{\mathrm{x}\right\}\:\mathrm{between}\:\mathrm{0}\:\mathrm{and}\:\mathrm{n}\in\mathbb{N}\:\mathrm{as}\:\mathrm{given}\:\mathrm{by} \\ $$$$\mathrm{A}_{\mathrm{n}} =\int_{\mathrm{0}} ^{\mathrm{n}} \left\{\mathrm{x}\right\}\mathrm{dx}. \\ $$$$ \\ $$$$ \\ $$$$\mathrm{M}.\mathrm{m} \\ $$

Question Number 180886 Answers: 1 Comments: 0

Question Number 180867 Answers: 1 Comments: 0

Question Number 180866 Answers: 1 Comments: 0

Question Number 180858 Answers: 1 Comments: 0

Question Number 180839 Answers: 1 Comments: 0

Find the derivatives f^′ (x) of the following function with respect to x: f(x)=Sin(π^(Sinx) +π^(Cosx) ). Mastermind

$$\mathrm{Find}\:\mathrm{the}\:\mathrm{derivatives}\:\mathrm{f}^{'} \left(\mathrm{x}\right)\:\mathrm{of}\:\mathrm{the} \\ $$$$\mathrm{following}\:\mathrm{function}\:\mathrm{with}\:\mathrm{respect}\:\mathrm{to}\:\mathrm{x}: \\ $$$$\mathrm{f}\left(\mathrm{x}\right)=\mathrm{Sin}\left(\pi^{\mathrm{Sinx}} +\pi^{\mathrm{Cosx}} \right). \\ $$$$ \\ $$$$\mathrm{Mastermind} \\ $$

Question Number 180838 Answers: 0 Comments: 1

Find all x∈R that are solutions to this question: 0=(1−x−x^2 −...)∙(2−x−x^2 −...) Mastermind

$$\mathrm{Find}\:\mathrm{all}\:\mathrm{x}\in\mathbb{R}\:\mathrm{that}\:\mathrm{are}\:\mathrm{solutions}\:\mathrm{to}\:\mathrm{this} \\ $$$$\mathrm{question}:\: \\ $$$$\mathrm{0}=\left(\mathrm{1}−\mathrm{x}−\mathrm{x}^{\mathrm{2}} −...\right)\centerdot\left(\mathrm{2}−\mathrm{x}−\mathrm{x}^{\mathrm{2}} −...\right) \\ $$$$ \\ $$$$\mathrm{Mastermind} \\ $$

Question Number 180837 Answers: 2 Comments: 0

Without using table, find the values of: (1/((1−(√3))^2 )) − (1/((1+(√3))^2 )) Mastermind

$$\mathrm{Without}\:\mathrm{using}\:\mathrm{table},\:\mathrm{find}\:\mathrm{the}\:\mathrm{values} \\ $$$$\mathrm{of}: \\ $$$$\frac{\mathrm{1}}{\left(\mathrm{1}−\sqrt{\mathrm{3}}\right)^{\mathrm{2}} }\:−\:\frac{\mathrm{1}}{\left(\mathrm{1}+\sqrt{\mathrm{3}}\right)^{\mathrm{2}} } \\ $$$$ \\ $$$$\mathrm{Mastermind} \\ $$

Question Number 180836 Answers: 1 Comments: 0

Determine A,B,C such that all of the following function intersect the point (2,2) ; f_1 (x)=Ax + 1, f_2 (x)=Bx^2 + 2, f_3 (x)=Cx^3 + 3 Mastermind

$$\mathrm{Determine}\:\mathrm{A},\mathrm{B},\mathrm{C}\:\mathrm{such}\:\mathrm{that}\:\mathrm{all}\:\mathrm{of}\:\mathrm{the} \\ $$$$\mathrm{following}\:\mathrm{function}\:\mathrm{intersect}\:\mathrm{the}\:\mathrm{point} \\ $$$$\left(\mathrm{2},\mathrm{2}\right)\:; \\ $$$$\mathrm{f}_{\mathrm{1}} \left(\mathrm{x}\right)=\mathrm{Ax}\:+\:\mathrm{1},\:\:\mathrm{f}_{\mathrm{2}} \left(\mathrm{x}\right)=\mathrm{Bx}^{\mathrm{2}} \:+\:\mathrm{2},\:\: \\ $$$$\mathrm{f}_{\mathrm{3}} \left(\mathrm{x}\right)=\mathrm{Cx}^{\mathrm{3}} \:+\:\mathrm{3} \\ $$$$ \\ $$$$\mathrm{Mastermind} \\ $$

Question Number 180801 Answers: 1 Comments: 0

Solve the Differential equation : (3xy+6y^2 )dx+(2x^2 +9xy)dy=0 Mastermind

$$\mathrm{Solve}\:\mathrm{the}\:\mathrm{Differential}\:\mathrm{equation}\:: \\ $$$$\left(\mathrm{3xy}+\mathrm{6y}^{\mathrm{2}} \right)\mathrm{dx}+\left(\mathrm{2x}^{\mathrm{2}} +\mathrm{9xy}\right)\mathrm{dy}=\mathrm{0} \\ $$$$ \\ $$$$\mathrm{Mastermind} \\ $$

Question Number 180713 Answers: 1 Comments: 7

Question Number 180683 Answers: 1 Comments: 0

(b) x + y + Kz = 2 3x + 4y + 2z = K 2x + 3y − z = 1

$$\left(\mathrm{b}\right)\:\mathrm{x}\:+\:\mathrm{y}\:+\:\mathrm{Kz}\:=\:\mathrm{2} \\ $$$$\:\:\:\:\mathrm{3x}\:+\:\mathrm{4y}\:+\:\mathrm{2z}\:=\:\mathrm{K} \\ $$$$\:\:\:\:\mathrm{2x}\:+\:\mathrm{3y}\:−\:\mathrm{z}\:=\:\mathrm{1} \\ $$

Question Number 180667 Answers: 3 Comments: 1

Question Number 180682 Answers: 1 Comments: 0

Determine the value of k such that the following system has (i) a Unique solution (ii) No solution (iii) More than one solution (a) Kx + y + z = 1 x +Ky + z = 1 x + y + Kz = 1

$$\mathrm{Determine}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:\mathrm{k}\:\mathrm{such}\:\mathrm{that}\:\mathrm{the} \\ $$$$\mathrm{following}\:\mathrm{system}\:\mathrm{has}\:\left(\mathrm{i}\right)\:\mathrm{a}\:\mathrm{Unique}\: \\ $$$$\mathrm{solution}\:\left(\mathrm{ii}\right)\:\mathrm{No}\:\mathrm{solution}\:\left(\mathrm{iii}\right)\:\mathrm{More}\:\mathrm{than} \\ $$$$\mathrm{one}\:\mathrm{solution} \\ $$$$ \\ $$$$\left(\mathrm{a}\right)\:\mathrm{Kx}\:+\:\mathrm{y}\:+\:\mathrm{z}\:=\:\mathrm{1} \\ $$$$\:\:\:\:\mathrm{x}\:+\mathrm{Ky}\:+\:\mathrm{z}\:=\:\mathrm{1} \\ $$$$\:\:\:\:\mathrm{x}\:+\:\mathrm{y}\:+\:\mathrm{Kz}\:=\:\mathrm{1} \\ $$

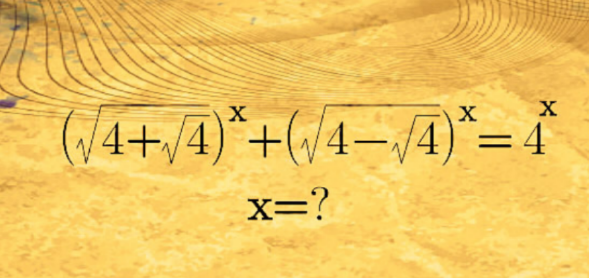
Question Number 180625 Answers: 1 Comments: 0

During the challenge Cup season. Team A scored 15 goals more than Team B. They have 121 goals between them. how many goals did each team score?

$$\mathrm{During}\:\mathrm{the}\:\mathrm{challenge}\:\mathrm{Cup}\:\mathrm{season}.\:\mathrm{Team} \\ $$$$\mathrm{A}\:\mathrm{scored}\:\mathrm{15}\:\mathrm{goals}\:\mathrm{more}\:\mathrm{than}\:\mathrm{Team}\:\mathrm{B}. \\ $$$$\mathrm{They}\:\mathrm{have}\:\mathrm{121}\:\mathrm{goals}\:\mathrm{between}\:\mathrm{them}. \\ $$$$\mathrm{how}\:\mathrm{many}\:\mathrm{goals}\:\mathrm{did}\:\mathrm{each}\:\mathrm{team}\:\mathrm{score}? \\ $$$$ \\ $$

Question Number 180621 Answers: 1 Comments: 0

Question Number 180549 Answers: 0 Comments: 0

Cross fertilization of 130 peas from different pure line yielded the following phenotype (GS, GW, and YW as follow GS only (36), GS and YW (15), all the three phenotype (9), GS and GW (14) YW and GW only (4). the number of those that have only YW or only GW are equal. a) How many peas have GW phenotype? b) How many peas have only one phenotype?

$$\mathrm{Cross}\:\mathrm{fertilization}\:\mathrm{of}\:\mathrm{130}\:\mathrm{peas}\:\mathrm{from} \\ $$$$\mathrm{different}\:\mathrm{pure}\:\mathrm{line}\:\mathrm{yielded}\:\mathrm{the}\:\mathrm{following} \\ $$$$\mathrm{phenotype}\:\left(\mathrm{GS},\:\mathrm{GW},\:\mathrm{and}\:\mathrm{YW}\:\mathrm{as}\:\mathrm{follow}\right. \\ $$$$\mathrm{GS}\:\mathrm{only}\:\left(\mathrm{36}\right),\:\mathrm{GS}\:\mathrm{and}\:\mathrm{YW}\:\left(\mathrm{15}\right),\:\mathrm{all}\:\mathrm{the} \\ $$$$\mathrm{three}\:\mathrm{phenotype}\:\left(\mathrm{9}\right),\:\mathrm{GS}\:\mathrm{and}\:\mathrm{GW}\:\left(\mathrm{14}\right) \\ $$$$\mathrm{YW}\:\mathrm{and}\:\mathrm{GW}\:\mathrm{only}\:\left(\mathrm{4}\right).\:\mathrm{the}\:\mathrm{number}\:\mathrm{of} \\ $$$$\mathrm{those}\:\mathrm{that}\:\mathrm{have}\:\mathrm{only}\:\mathrm{YW}\:\mathrm{or}\:\mathrm{only}\:\mathrm{GW} \\ $$$$\mathrm{are}\:\mathrm{equal}. \\ $$$$\left.\mathrm{a}\right)\:\mathrm{How}\:\mathrm{many}\:\mathrm{peas}\:\mathrm{have}\:\mathrm{GW}\:\mathrm{phenotype}? \\ $$$$\left.\mathrm{b}\right)\:\mathrm{How}\:\mathrm{many}\:\mathrm{peas}\:\mathrm{have}\:\mathrm{only}\:\mathrm{one}\: \\ $$$$\mathrm{phenotype}? \\ $$

Pg 14 Pg 15 Pg 16 Pg 17 Pg 18 Pg 19 Pg 20 Pg 21 Pg 22 Pg 23

Contact: info@tinkutara.com